Codeforces Round div2 #541 题解

codeforces Round #541

abstract:

I构造题可能代码简单证明很难

II拓扑排序

III并查集 启发式排序，带链表

IV dp 处理字符串递推问题

V 数据结构巧用：于二叉树同构

VI更新了头文件，将很难敲的东西放到define里面，初始化数组可以a[100]={};

C

题意

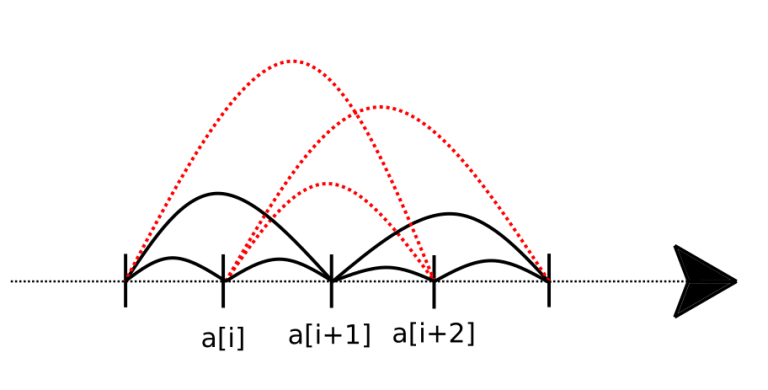
给你100个人，让你将它们围成一个圆，使得：“任意相邻的两人身高差的绝对值” 中的最大值 最小

---

题解

显然的构造方法:先排序，让所有人1 2 报数，报2的出列，排尾变排头接到报 1 的原队列后面

证明：

显然这样的构造方法保证身高差最大为 max{（a[i+2]-a[i]) }（i=1..n,环状,a[i]升序）；

我们可以说明对于任意的i，身高差至少为（a[i+2]-a[i]），

如果我们将每个人看成一个点，相邻关系看成一条无向边，那么可以作图如下：

不难发现题目等价于构造一条哈密尔顿回路（i.e.从一点出发，走过所有点，且每个点只经过一次，再回到起点）。

反证法：如果存在一条更优的路线，那么我们就不能使用a[i+2]-a[i]这条边以及比这条长的所有边。

同时我们发现去掉这些边以后，a[i+1]变成了割点——从左边到右边必须经过，回到左边时还要经过，违反了初始约定（哈密尔顿回路）。

矛盾。

得证。

---

代码

---

D

题意

有两行数，不知道他们的实际值，但知道两行数含有的数字个数,以及行与行所有数字两两之间的大小关系，求一组解使得最大的数最小，若无解特判掉。

input
3 3
>>>
<<<
>>>  

output
Yes
3 1 3
2 2 2

---

题解

拓扑排序板题加并查集

建图，从小的数向大的数建有向边，然后拓扑排序，输出他们的优先级即可。

唯一的trick是关系中有=，我们只要把=关系的结点缩点即可，具体实现用并查集，输出时再还原。

拓扑排序用的是khan算法（还有一种倒着dfs的算法)i.e. 队列压入0点，bfs一下，访问到某个点时，将其入度减1，减到0时，压到队列尾部。判断是否有环的方法是记录入栈的点数（每个点只会被压入一次），如果小于总点数，则说明有环。

codeforces的bug：用了加速cin后，puts("")输出的东西会跑到在cout总输出的后面？？！！！

---

代码

//邻接表建图
#include<algorithm>
#include<iostream>
#include<sstream>
#include<stdlib.h>
#include<string.h>
#include<assert.h>
#include<math.h>
#include<stdio.h>
#include<vector>
#include<queue>
#include<string>
#include<ctime>
#include<stack>
#include<map>
#include<set>
#include<list>
using namespace std;
#define rep(i,j,k) for(int i = (int)j;i <= (int)k;i ++)
#define REP(i,j,k) for(int i = (int)j;i < (int)k;i ++)
#define per(i,j,k) for(int i = (int)j;i >= (int)k;i --)
#define debug(x) cerr<<#x<<" = "<<(x)<<endl
#define mmm(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define MD(x) x%=mod
//#define x first
//#define y second
typedef double db;
typedef long long ll;
const int MAXN = 30;;
const int maxn = 2e3+2;
const int INF = 1e9;
const db eps = 1e-7;
const int mod = 1e9 + 7;

vector<int> a, b;
//a[maxn], b[maxn];
int A[maxn];
int n,m;
int fa[maxn];
int vis[maxn], dep[maxn],ind[maxn],id[maxn],ans[maxn],ians[maxn];
void init() { for (int i = 1; i <= n+m; i++) fa[i] = i,id[i]=i; }
int find(int x) { if (fa[x] == x) { return x; }return fa[x] = find(fa[x]); }
void un(int x, int y) { int xx = find(x), yy = find(y); fa[yy] = x; }

char mmp[maxn][maxn];
vector<int> E[maxn];
int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);

	cin >> n>>m;

	//n += m;
	init();
	rep(i, 1,n )cin >> mmp[i]+1;
	rep(i, 1, n)rep(j, 1,m) if (mmp[i][j] == '=') {
		un(i, j + n);
	}

	rep(i, 1, n)rep(j, 1, m) {
		int x = find(i), y = find(j + n);
		if (mmp[i][j] == '<') {
			E[x].push_back(y);
			ind[y]++;
		}
		if (mmp[i][j] == '>') {
			E[y].push_back(x);
			ind[x]++;
		}
	}

	int cnt = 0;
	rep(i, 1, m + n)if (fa[i] == i)E[0].push_back(i), ind[i]++, cnt++;

	queue<int> Q;
	Q.push(0);
	int tmp = 0;
	vis[0] = 1;
	while (!Q.empty()) {
		int u = Q.front();
		Q.pop();// vis[u] = 1;
		for (int i = 0; i < E[u].size(); i++) {
			int v = E[u][i];
			if (fa[v] == v) {
				ind[v]--;
				if (ind[v] == 0) {
					Q.push(v); tmp++;
					dep[v] = dep[u] + 1;
				}
			}
		}

	}
	//rep(i, 1, n + m)debug(dep[i]);
	if (tmp < cnt) {
		puts("No"); return 0;
	}
	cout << "Yes" << endl;
	rep(i, 1, n + m) { ians[i] = dep[i]; }
	rep(i, 1, n + m) { int u = find(i); ans[i] = ians[u]; }
	rep(i, 1, n)cout << ans[i] << ' '; cout << endl;
	rep(j, 1, m)cout << ans[n+j] << ' ';
	cout << endl;
	//cin >> n;
}
/*

*/

---

E

题意

定义字符串的乘法： s1*s2就是将s2插入s1的所有相邻字符之间，再在首尾接上s2

sample:
bnn*a=abanana
a*b*a=abaaaba

现在给你1e5个字符串，问最终串的结果中所有字母都相同的最长子串（后面称作重复子串）的长度。

---

题解

考虑不求出最终串如何维护最长串。 发现每次乘上一个串，我们只要关注这个串的最长重复前后缀即可，然后就可以从n个串推到n+1个串的乘积。

于是考虑dp，f[i]代表前i个串的乘积中最长的重复子串，对每个串，线性处理出最长前后缀pre,suf以及串内最长重复子串len，f[i]=max(len,pre+suf+1),

我们发现这个公式的前提是所有字符都相同，所以我们给f加一维，f[i][j]，其中j表示字符（'a'..'z')

于是我们得出递推公式(令当前串s的s.length()为L)：

if(pre==L)f[i][j]=max(len,L*f[i-1][j]+L+f[i][j])

else if(f[i-1][j]) f[i][j]=max(len,pre+1+suf);

最后更新答案要注意是对f[n]['a'..'z']更新，因为之前的答案可能比之后的大。

---

代码

#include<algorithm>
#include<iostream>
#include<sstream>
#include<stdlib.h>
#include<string.h>
#include<assert.h>
#include<math.h>
#include<stdio.h>
#include<vector>
#include<queue>
#include<string>
#include<ctime>
#include<stack>
#include<map>
#include<set>
#include<list>
using namespace std;
#define rep(i,j,k) for(int i = (int)j;i <= (int)k;i ++)
#define REP(i,j,k) for(int i = (int)j;i < (int)k;i ++)
#define per(i,j,k) for(int i = (int)j;i >= (int)k;i --)
#define debug(x) cerr<<#x<<" = "<<(x)<<endl
#define mmm(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define MD(x) x%=mod
#define FAST_IO ios_base::sync_with_stdio(false); cin.tie(nullptr)
#define precise(x) fixed << setprecision(x)

//#define x first
//#define y second
typedef double db;
typedef long long ll;
const int MAXN = 256;;
const int maxn = 2e5+2;
const int INF = 1e9;
const db eps = 1e-7;
const int mod = 1e9 + 7;

//a[maxn], b[maxn];
int A[maxn];
int n,m;
int fa[maxn];
void init() { for (int i = 1; i <= n + m; i++) fa[i] = i; }
int find(int x) { if (fa[x] == 0) { return x; }return fa[x] = find(fa[x]); }
//int Find(int u) { return fa[u] == 0 ? u : fa[u] = Find(fa[u]); }
void un(int x, int y) { int xx = find(x), yy = find(y); fa[yy] = x; }

vector<int> E[maxn];
pair<int, int> son[maxn];
string s;
int f[maxn][256];//f[i][j] 代表前i个串的乘积中 只有字符j的最长子串长度。
int main() {
	FAST_IO;
	cin >> n;
	int ans = 0;
	rep(i, 1, n) {
		cin >> s;
		int l = s.length(), t[256] = {}, r[256] = {};
		rep(j, 0, l - 1) {
			if ((j&&s[j - 1] == s[j]))t[s[j]]++; else t[s[j]] = 1;
			r[s[j]] = max(r[s[j]], t[s[j]]);
		}
		rep(j, 'a','z') {
			f[i][j] = r[j];
			int t1 = 0, t2 = l - 1; while (s[t1] == j && t1 < l)t1++;
			while (s[t2] == j && t2 > t1)t2--;
			if (t1 == l)f[i][j] = max(f[i][j], f[i - 1][j] * l + l + f[i - 1][j]);//递推计算乘积中最长序列
			else if (f[i - 1][j])f[i][j] = max(f[i][j], t1 + l - t2);
			if (i == n)ans = max(ans, f[i][j]);
		}
	}
	cout << ans << endl;
	cin >> n;
}
/*
.

*/

---

F

题意

有一行数，不知道每个数具体的数值，现在把每个数看成一个集合，给你一系列合并操作x y,表示合并xy所在的集合，已知每次只能合并相邻的集和，求初始的这行数的可能解，保证有解。

---

题解

算法如下：

将集合看成二叉树，我们每次合并两个集合时建立一个新的结点，作为新集合的根。 这里用并查集O（1）地查询到根，并做合并操作。

执行完所有合并之后得到了一颗二叉树，对其进行先序遍历，到叶子时输出数字即可。

证明：

叶子对应于原数组的数。

每个新的结点对应于一个合并操作，

二叉树上连着根的两棵子树是相邻的，对应于每次合并相邻的集合。

所以叶子从左到右对应着一个解，

用先序即可输出。

---

代码

#include<algorithm>
#include<iostream>
#include<sstream>
#include<stdlib.h>
#include<string.h>
#include<assert.h>
#include<math.h>
#include<stdio.h>
#include<vector>
#include<queue>
#include<string>
#include<ctime>
#include<stack>
#include<map>
#include<set>
#include<list>
using namespace std;
#define rep(i,j,k) for(int i = (int)j;i <= (int)k;i ++)
#define REP(i,j,k) for(int i = (int)j;i < (int)k;i ++)
#define per(i,j,k) for(int i = (int)j;i >= (int)k;i --)
#define debug(x) cerr<<#x<<" = "<<(x)<<endl
#define mmm(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define MD(x) x%=mod
#define FAST_IO ios_base::sync_with_stdio(false); cin.tie(nullptr)
#define precise(x) fixed << setprecision(x)

//#define x first
//#define y second
typedef double db;
typedef long long ll;
const int MAXN = 30;;
const int maxn = 3e5+2;
const int INF = 1e9;
const db eps = 1e-7;
const int mod = 1e9 + 7;

//a[maxn], b[maxn];
int A[maxn];
int n,m;
int fa[maxn];
void init() { for (int i = 1; i <= n + m; i++) fa[i] = i; }
int find(int x) { if (fa[x] == 0) { return x; }return fa[x] = find(fa[x]); }
//int Find(int u) { return fa[u] == 0 ? u : fa[u] = Find(fa[u]); }
void un(int x, int y) { int xx = find(x), yy = find(y); fa[yy] = x; }

vector<int> E[maxn];
pair<int, int> son[maxn];
void dfs(int u) {
	if (u <= n) {
		cout << u << ' ';
		return;
	}
	dfs(son[u].first); dfs(son[u].second);
}
int main() {
	FAST_IO;

	cin >> n;
	int u, v;
	//init();
	rep(i, 1, n-1) {
		cin >> u >> v;
		u = find(u); v = find(v);
		fa[u] = fa[v] = n + i;
		son[n + i] = { u,v };
	}
	dfs(find(1));
	cin >> n;
}
/*
Simple explanation: when we merge 2 sets, we create a new node stands for the whole set and set its two sons to that 2 sets.
After all operations it will become a tree because answer always exists.
Use DFS to travel this tree, and every time when we meet a leaf node just print it.
It's correct because for every merge operation the 2 operands are sons of a new node and that guarantees the 2 part must be neighbors in the final output.

*/

//another simplest solution is based on a set-size version of rank heuristic
//uses standard disjoint-set data structure storing lists of elements in each set
struct DSU {
    vector<int> par;
    vector<int> sz;
    vector<list<int>> parts;
    DSU(int n) {
        FOR(i, 0, n) {
            par.pb(i);
            sz.pb(1);
            parts.pb({i});
        }
    }

    int find(int a) {
        return par[a] = par[a] == a ? a : find(par[a]);
    }

    bool same(int a, int b) {
        return find(a) == find(b);
    }

    void unite(int a, int b) {
        a = find(a);
        b = find(b);
        if(a == b) return;
        if(sz[a] > sz[b]) swap(a, b);
        // sz[a] <= sz[b]
        sz[b] += sz[a];
        par[a] = b;
        parts[b].splice(parts[b].end(), parts[a]);
    }
};

int main() {
    FAST_IO;
    startTime();

    int n;
    cin >> n;
    DSU dsu(n);
    FOR(i, 0, n-1) {
        int u, v;
        cin >> u >> v;
        u--, v--;
        u = dsu.find(u);
        v = dsu.find(v);
        dsu.unite(u, v);
    }
    auto l = dsu.parts[dsu.find(0)];
    for(auto x : l) {
        cout << x+1 << " ";
    }
    cout << endl;

    timeit("Finished");
    return 0;
}

---