[jzoj]1229.Hanoi

Link

　　https://jzoj.net/senior/#main/show/1229

Description

　　Mpq 小时候只玩过俄罗斯方块这个经典的小游戏，当时他还不知道Hanoi 究竟是什么东西。话说当Mpq 第一次认识Hanoi 是在初三那年的联赛。由于Mpq 之前并不知道Hanoi 是什么东西，所以那一年他做完前三题之后很郁闷地坐了1 个半小时。。。好了，现在Mpq 成长了，他已经解决当年联赛那道Hanoi 了，在前几个月，他又发现一道关于Hanoi 的题目了，很幸运的是这个题目他知道怎么做了。。。然后为了让大家体验一下Mpq 初三联赛那种无奈的感觉，所以，这道题就神奇地出现在你们眼前。

　　Task：赶快AC 这道题目，然后你就可以狂鄙视，甚至是无视Mpq 的存在了！！！　　　

　　哎，吹着吹着发现我还没把题目写下来。。。。
　　现在给你M 根柱子，初始的时候有N 个大小不一样的盘插在第一根柱子上面。同样地，规格大的盘子不能放在规格比它小的盘子上面。问最少需要多少次的移动才能将这N 个盘从第一根柱子移动到最后一根柱子上面？

Solution

30分

　　因为m=3的情况的解是有规律可循的，所以输出2ⁿ-1即可

100分

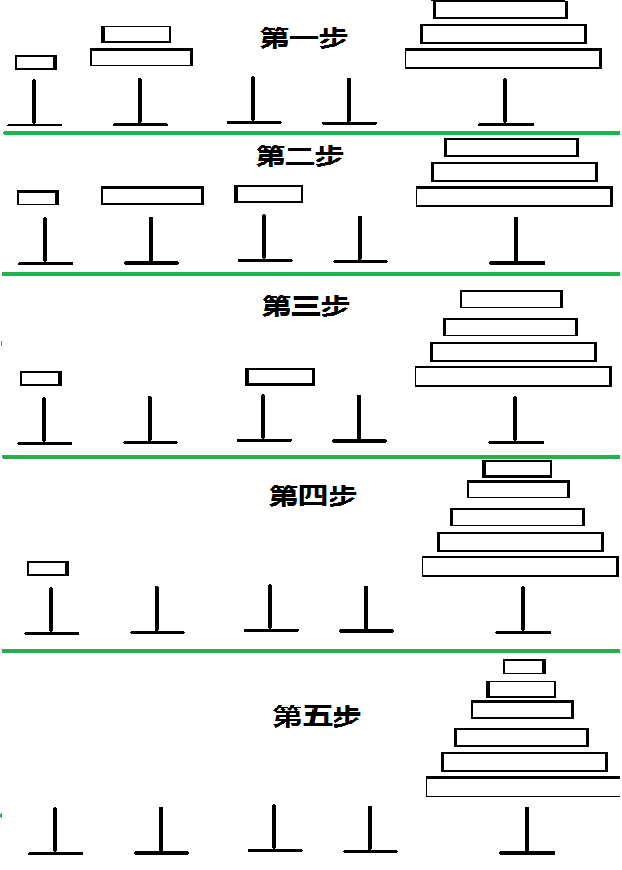
　　对于完整一次的汉诺塔操作，显然一定会在第2~n-1中某一根柱子上，堆砌起一堆按顺序的盘子，然后再将原本在第一根柱子的盘子均摊到其他没有盘子的柱子处（均摊指每个位置，除了最先堆砌起来那堆盘子所在的柱子外，其他柱子都只有1个盘子，且最大的盘子在第n根柱子处），然后依次将刚才均摊的盘子，放到最后一个柱子，再把最先堆砌起的盘子，均摊，依次摆放到最后一根柱子上。想不懂可以看下图

　　①显然一定会在第2~n-1中某一根柱子上，堆砌起一堆按顺序的盘子

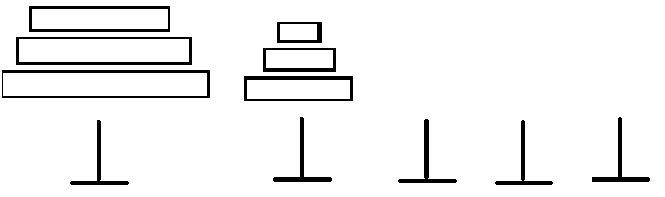
　　②然后再将原本在第一根柱子的盘子均摊到其他没有盘子的柱子处（均摊指每个位置，除了最先堆砌起来那堆盘子所在的柱子外，其他柱子都只有1个盘子，且最大的盘子在第n根柱子处）

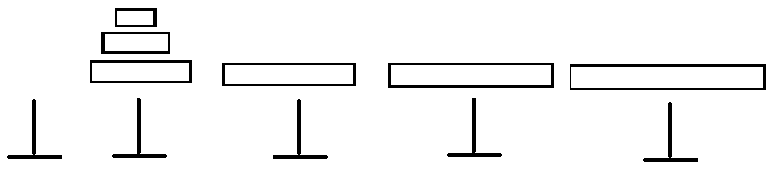
　　③然后依次将刚才均摊的盘子，放到最后一个柱子

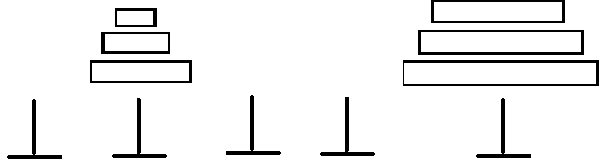
　　④再把最先堆砌起的盘子，均摊，依次摆放到最后一根柱子上

　　我们设f[i,j]表示你用i个盘子，j根柱子做汉诺塔的最优方案。

　　设g[i,j]表示你用i个盘子，j根柱子做汉诺塔的最优方案，是在第2~n-1中某一根柱子上，堆砌起g[i,j]个按大小顺序叠起来的盘子。

　　那么，假设柱子相同，盘子不定，考虑每次放一个盘子上去，这样就有两种情况

　　第一种：就是这个盘子放在大盘子处，也就是说，他在上面的①流程中，是没有操作的，那么，这时第一次堆砌起来的盘子数量，就是少一个盆子时堆砌的数量，是g[i-1,j]

　　第二种，就是把这个盘子放在较小盘子处，就是在①流程中执行操作的盘子，换句话说，就是第一次堆砌的盘子其中一个，那么这就比少一个盘子时第一次堆砌的盘子数量多了1，就是g[i-1,j]+1

　　我们设当前第一次挪出去的盘子有k个，k=g[i-1,j]~g[i-1,j]+1（上面说过），那么显然

　　f[i,j]=min(f[k,j]+f[i-k,j-1]+f[k,j])

　　f[k,j]表示你先把k个挪出去摆成一堆的最优解

　　f[i-k,j-1]表示你把剩下的i-k个盘子，均摊后，再挪到最后一根柱子，相当于直接整个柱子的盘子移到最后一个柱子。这时因为第一次挪的盘子占了1根柱子，所以只剩下j-1根柱子

　　最后的f[k,j]表示你第一次挪出去摆成一堆的盘子

　　每次的g[i,j]为较优的k

　　很成功，我们解完这道题目了，网上有很多关于汉诺塔的探究，不过都不是这种算法的，都是只能求固定柱子的最优解。希望这篇博客可以帮到大家。

Code

var
        n,m,i,j,k:longint;
        f,g:array[..,..] of qword;
begin
        readln(n,m);

        for i:= to  do
        begin
                f[i,]:=f[i-,]*+;
                g[i,]:=i-;
        end;

        for i:= to n do
        begin
                for j:= to m do
                        begin
                                f[i,j]:=maxlongint*maxlongint;
                                k:=g[i-,j];
                                if f[i,j]>f[k,j]*+f[i-k,j-] then
                                begin
                                        f[i,j]:=f[k,j]*+f[i-k,j-];
                                        g[i,j]:=k;
                                end;

                                k:=g[i-,j]+;
                                if f[i,j]>f[k,j]*+f[i-k,j-] then
                                begin
                                        f[i,j]:=f[k,j]*+f[i-k,j-];
                                        g[i,j]:=k;
                                end;
                        end;
        end;

        writeln(f[n,m]);
end.