斯坦福大学公开课机器学习：Neural network-model representation（神经网络模型及神经单元的理解）

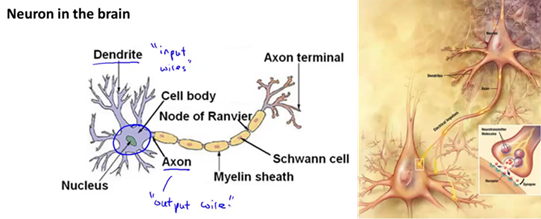
神经网络是在模仿大脑中的神经元或者神经网络时发明的。因此，要解释如何表示模型假设，我们先来看单个神经元在大脑中是什么样的。如下图，我们的大脑中充满了神经元，神经元是大脑中的细胞，其中有两点值得我们注意，一是神经元有细胞主体，二是神经元有一定数量的输入神经。这些输入神经叫做树突，可以把它们想象成输入电线，它们接收来自其他神经元的信息，神经元的输出神经叫做轴突，这些输出神经是用来给其他神经元传递信号或者传送信息的。简而言之，神经元是一个计算单元，它从输入神经接受一定数目的信息，并做一些计算，然后将结果通过它的轴突传送到其他节点，或者大脑中的其他神经元。右下图是一组神经元的示意图，神经元利用微弱的电流进行沟通，这些弱电流也称作动作电位，其实就是一些微弱的电流，所以如果神经元想要传递一个消息，它就会就通过它的轴突发送一段微弱电流给其他神经元。这是一条连接到输入神经或者连接另一个神经元树突的神经，接下来这个神经元接收这条消息做一些计算。它有可能会反过来将在轴突上的自己的消息传给其他神经元。这就是所有人类思考的模型：我们的神经元把自己的收到的消息进行计算并向其他神经元传递信息。这也是我们的感觉和肌肉运转的原理，如果你想活动一块肌肉，就会触发一个神经元给你的肌肉发送脉冲，并引起你的肌肉收缩。如果一些感官，比如说眼睛想要给大脑传递一个消息，那么它就像这样发送电脉冲给大脑。

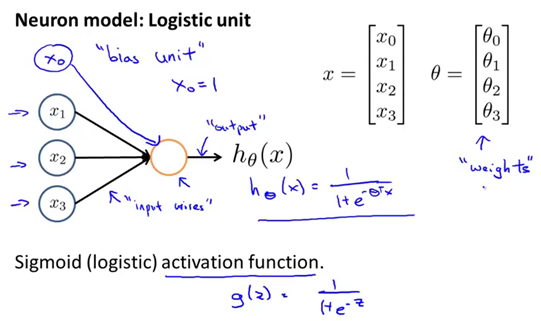
Neuron model:logistic unit

在一个神经网络里，或者说在我们在电脑上实现的人工神经网络里，我们将使用一个非常简单的模型，来模拟神经元的工作。我们将神经元模拟成一个逻辑单元,当画一个黄色圆圈时（黄色小圈代表一个单一的神经元，下图所示），你应该把它想象成作用类似于神经元的东西，然后我们通过它的树突或者说它的输入神经传递给它一些信息，然后神经元做一些计算，并通过它的输出神经，即它的轴突输出计算结果，当画一个像这样的图表时，就表示对h(x)的计算，h(x)等于1除以1+e的负θ转置乘以x。通常，x和θ是参数向量。这是一个简单的模型，甚至说是一个过于简单的模拟神经元的模型。它被输入x1、x2和x3，然后输出一些类似这样的结果。当绘制一个神经网络时，通常只绘制输入节点x1、x2和x3。但有时也可以这样做：增加一个额外的节点x0，这个x0节点，有时也被称作偏置单位或偏置神经元，但因为x0总是等于1，所以有时候会画出它，有时不会画出，这取决于它是否对例子有利。现在讨论最后一个关于神经网络的术语，有时我们会说这是一个神经元，一个有s型函数或者逻辑函数作为激励函数的人工神经元。在神经网络术语中，激励函数只是对类似非线性函数g(z)的另一个术语称呼，g(z)等于1除以1加e的-z次方。到目前为止，θ一直被称为模型的参数，以后大概会继续将这个术语与“参数”相对应，而不是与神经网络。在关于神经网络的文献里，有时可能会看到人们谈论一个模型的权重，权重其实和模型的参数是一样的东西。

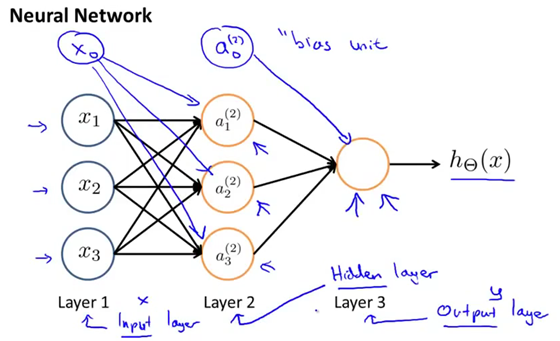
神经网络其实就是不同的神经元组合在一起的集合，具体来说，就是我们输入单元x1、x2和x3（如下图），有时候也可以画上额外的节点x0. 这里有个神经元，我们写成a1⁽²⁾，a2⁽²⁾，a3⁽²⁾。然后再次说明，我们可以在这里添加一个a0，和一个额外的偏度单元，它的值永远是1，最后我们在最后一层有第三个节点，正是这第三个节点，输出假设函数h(x)计算的结果。再多说一点关于神经网络的术语网络中的第一层也被称为输入层，因为我们在这一层输入我们的特征项x1、x2和x3，最后一层也称为输出层，中间的两层也被称作隐藏层，隐藏层不是一个很合适的术语，但是直觉上我们知道在监督学习中，你能看到输入，也能看到正确的输出。而隐藏层的值，你在训练集里是看不到的。它的值不是x，也不是y，所以我们叫它隐藏层。稍后我们会看到神经网络可以有不止一个的隐藏层，但在这个例子中，我们有一个输入层—第1层、一个隐藏层—第2层和一个输出层—第3层。但实际上任何非输入层或非输出层的层就被称为隐藏层。

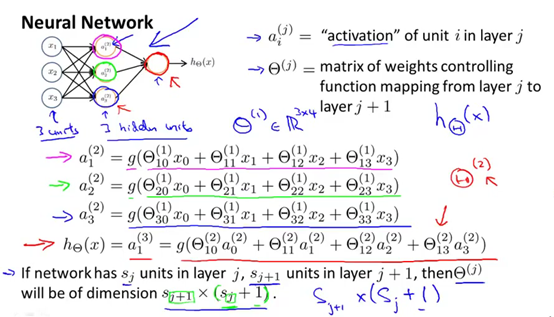
为了解释神经网络具体的计算步骤，下图有些记号要解释，使用a上标(j)、下标i表示第j层的第i个神经元或单元。具体来说，a上标（2）、下标1，表示第2层的第一个激活值，所谓激励(activation)是指由一个具体神经元读入计算并输出的值。此外，神经网络被这些矩阵参数化，θ上标(j) 将成为一个波矩阵控制着从一层，比如说从第一层到第二层或者第二层到第三层的作用。下图的第一个隐藏单元是这样计算它的值的：a(2)1等于s函数或者说s激励函数，也叫做逻辑激励函数，作用在这种输入的线性组合上的结果。第二个隐藏单元，等于s函数作用在这个线性组合上的值。参数矩阵控制了来自三个输入单元、三个隐藏单元的映射。因此θ1的维数将变成3。θ1将变成一个3乘4维的矩阵。更一般的, 如果一个网络在第j层有s_j个单元，在j+1层有s_j+1个单元，那么矩阵θ(j)，即控制第j层到第j+1层映射的矩阵的维度为s_j+1* (s_j+1)。所以θ(j)的维度是s_j+1行、s_j+1列。