OpenCASCADE Linear Extrusion Surface

OpenCASCADE Linear Extrusion Surface

eryar@163.com

Abstract. OpenCASCADE linear extrusion surface is a generalized cylinder. Such a surface is obtained by sweeping a curve (called the “extruded curve” or “basis”) in a given direction (referred to as the direction of extrusion and defined by a unit vector). The u parameter is along the extruded curve. The v parameter is along the direction of extrusion. The form of a surface of linear extrusion is generally a ruled surface. It can be a cylindrical surface, or a planar surface.

Key Words. OpenCASCADE, Extrusion Surface, Sweeping

1. Introduction

一般柱面（The General Cylinder）可以由一段或整个圆弧沿一个方向偏移一定的距离得到。如下图所示：

Figure 1.1 Extrusion Shapes

当将顶点拉伸时，会生成一条边；当将边拉伸时，会生成面；当将Wire拉伸时，会生成Shell，当将面拉伸时，会生成体。当将曲线沿一个方向拉伸时，会形成一个曲面，如果此方向为直线，则会生成一般柱面。如果此方向是曲线时，会生成如下图所示曲面：

Figure 1.2 Swept surface/ loft surface

本文主要介绍将曲线沿直线方向拉伸的算法，即一般柱面生成算法。并将生成的曲面在OpenSceneGraph中进行显示。

2.Cylinder Surface Definition

设 W是一个单位向量，C(u)是定义在节点矢量U上，权值为wi的p次NURBS曲线。我们要得到一般柱面S(u,v)的表达式，S(u,v)是通过将 C(u)沿方向W平行扫描（sweep）距离d得到的。记扫描方向的参数为v, 0<v<1，显然，S(u,v)必须满足以下两个条件：

v 对于固定的u0, S(u0, v)为由C(u0)到C(u0)+dW的直线段；

v 对于固定的v0：

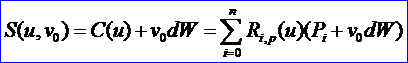
所要求的柱面的表达式为：

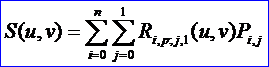
S(u,v)定义在节点矢量U和V上，这里V＝{0，0，1，1}，U为C(u)的节点矢量。控制顶点由Pi,0=Pi和Pi,1=Pi+dW给出，权值wi,0=wi,1=wi。如下图所示为一般柱面：

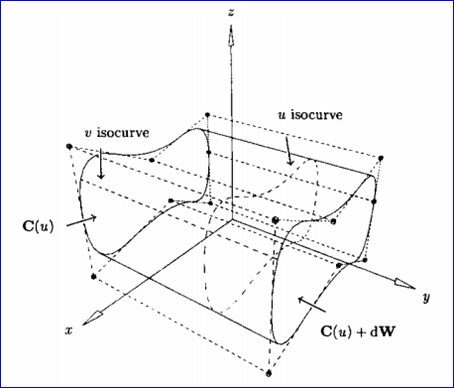
Figure 2.1 A general cylinder obtained by translating C(u) a distance d along W.

其中OpenCASCADE中一般柱面的表达式如下所示：

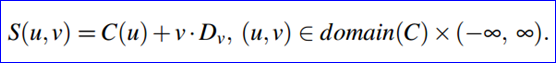
其取值范围的代码如下所示：

//=======================================================================
//function : Bounds
//purpose  :
//=======================================================================
void Geom_SurfaceOfLinearExtrusion::Bounds ( Standard_Real& U1,
                         Standard_Real& U2,
                         Standard_Real& V1,
                         Standard_Real& V2 ) const {

  V1 = -Precision::Infinite();  V2 = Precision::Infinite();
  U1 = basisCurve->FirstParameter();  U2 = basisCurve->LastParameter();
}

由上代码可知，参数在v方向上是趋于无穷的；在u方向上参数的范围为曲线的范围。计算柱面上点的方法代码如下所示：

//=======================================================================
//function : D0
//purpose  :
//=======================================================================
void Geom_SurfaceOfLinearExtrusion::D0 (const Standard_Real U,
                                        const Standard_Real V,
                                        Pnt& P)  const {

  XYZ Pxyz = direction.XYZ();
  Pxyz.Multiply (V);
  Pxyz.Add (basisCurve->Value (U).XYZ());
  P.SetXYZ(Pxyz);
}

即将柱面上点先按V方向来计算，再按U方向来计算，最后将两个方向的值相加即得到柱面上的点。

由上述代码可知，OpenCASCADE中一般柱面没有使用NURBS曲面来表示。根据这个方法，可以将任意曲线沿给定的方向来得到一个柱面，这个曲线可以是直线、圆弧、圆、椭圆等。关于柱面上更多算法，如求微分等，可以参考源程序。

3.Display the Surface

还是在OpenSceneGraph中来对一般柱面进行可视化，来验证结果。因为OpenSceneGraph的简单易用，显示曲面的程序代码如下所示：

/*
*    Copyright (c) 2013 to current year. All Rights Reserved.
*
*           File : Main.cpp
*         Author : eryar@163.com
*           Date : 2014-11-23 10:18
*        Version : OpenCASCADE6.8.0
*
*    Description : Test the Linear Extrusion Surface of OpenCASCADE.
*
*      Key Words : OpenCascade, Linear Extrusion Surface, General Cylinder
*
*/

// OpenCASCADE.
#define WNT
#include <Precision.hxx>

#include <gp_Circ.hxx>

#include <Geom_SurfaceOfLinearExtrusion.hxx>

#include <GC_MakeCircle.hxx>
#include <GC_MakeSegment.hxx>
#include <GC_MakeArcOfCircle.hxx>

#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKG3d.lib")
#pragma comment(lib, "TKGeomBase.lib")

// OpenSceneGraph.
#include <osgViewer/Viewer>
#include <osgViewer/ViewerEventHandlers>

#include <osgGA/StateSetManipulator>

#pragma comment(lib, "osgd.lib")
#pragma comment(lib, "osgGAd.lib")
#pragma comment(lib, "osgViewerd.lib")

const double TOLERANCE_EDGE = 1e-;
const double APPROXIMATION_DELTA = 0.05;

/**
* @brief Render 3D geometry surface.
*/
osg::Node* BuildSurface(const Handle_Geom_Surface& theSurface)
{
    osg::ref_ptr<osg::Geode> aGeode = new osg::Geode();

    Standard_Real aU1 = 0.0;
    Standard_Real aV1 = 0.0;
    Standard_Real aU2 = 0.0;
    Standard_Real aV2 = 0.0;
    Standard_Real aDeltaU = 0.0;
    Standard_Real aDeltaV = 0.0;

    theSurface->Bounds(aU1, aU2, aV1, aV2);

    // trim the parametrical space to avoid infinite space.
    Precision::IsNegativeInfinite(aU1) ? aU1 = -1.0 : aU1;
    Precision::IsInfinite(aU2) ? aU2 = 1.0 : aU2;

    Precision::IsNegativeInfinite(aV1) ? aV1 = -1.0 : aV1;
    Precision::IsInfinite(aV2) ? aV2 = 1.0 : aV2;

    // Approximation in v direction.
    aDeltaU = (aU2 - aU1) * APPROXIMATION_DELTA;
    aDeltaV = (aV2 - aV1) * APPROXIMATION_DELTA;

    for (Standard_Real u = aU1; (u - aU2) <= TOLERANCE_EDGE; u += aDeltaU)
    {
        osg::ref_ptr<osg::Geometry> aLine = new osg::Geometry();
        osg::ref_ptr<osg::Vec3Array> aPoints = new osg::Vec3Array();

        for (Standard_Real v = aV1; (v - aV2) <= TOLERANCE_EDGE; v += aDeltaV)
        {
            gp_Pnt aPoint = theSurface->Value(u, v);

            aPoints->push_back(osg::Vec3(aPoint.X(), aPoint.Y(), aPoint.Z()));
        }

        // Set vertex array.
        aLine->setVertexArray(aPoints);
        aLine->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::LINE_STRIP, , aPoints->size()));

        aGeode->addDrawable(aLine.get());
    }

    // Approximation in u direction.
    for (Standard_Real v = aV1; (v - aV2) <= TOLERANCE_EDGE; v += aDeltaV)
    {
        osg::ref_ptr<osg::Geometry> aLine = new osg::Geometry();
        osg::ref_ptr<osg::Vec3Array> aPoints = new osg::Vec3Array();

        for (Standard_Real u = aU1; (u - aU2) <= TOLERANCE_EDGE; u += aDeltaU)
        {
            gp_Pnt aPoint = theSurface->Value(u, v);

            aPoints->push_back(osg::Vec3(aPoint.X(), aPoint.Y(), aPoint.Z()));
        }

        // Set vertex array.
        aLine->setVertexArray(aPoints);
        aLine->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::LINE_STRIP, , aPoints->size()));

        aGeode->addDrawable(aLine.get());
    }

    return aGeode.release();
}

/**
* @brief Build the test scene.
*/
osg::Node* BuildScene(void)
{
    osg::ref_ptr<osg::Group> aRoot = new osg::Group();

    // test the linear extrusion surface.
    // test linear extrusion surface of a line.
    Handle_Geom_Curve aSegment = GC_MakeSegment(gp_Pnt(3.0, 0.0, 0.0), gp_Pnt(6.0, 0.0, 0.0));
    Handle_Geom_Surface aPlane = new Geom_SurfaceOfLinearExtrusion(aSegment, gp::DZ());

    aRoot->addChild(BuildSurface(aPlane));

    // test linear extrusion surface of a arc.
    Handle_Geom_Curve aArc = GC_MakeArcOfCircle(gp_Circ(gp::ZOX(), 2.0), 0.0, M_PI, true);
    Handle_Geom_Surface aSurface = new Geom_SurfaceOfLinearExtrusion(aArc, gp::DY());

    aRoot->addChild(BuildSurface(aSurface));

    // test linear extrusion surface of a circle.
    Handle_Geom_Curve aCircle = GC_MakeCircle(gp::XOY(), 1.0);
    Handle_Geom_Surface aCylinder = new Geom_SurfaceOfLinearExtrusion(aCircle, gp::DZ());

    aRoot->addChild(BuildSurface(aCylinder));

    return aRoot.release();
}

int main(int argc, char* argv[])
{
    osgViewer::Viewer aViewer;

    aViewer.setSceneData(BuildScene());

    aViewer.addEventHandler(new osgGA::StateSetManipulator(
        aViewer.getCamera()->getOrCreateStateSet()));
    aViewer.addEventHandler(new osgViewer::StatsHandler);
    aViewer.addEventHandler(new osgViewer::WindowSizeHandler);

    return aViewer.run();

    return ;
}

上述显示方法只是显示线框的最简单的算法，只为验证一般柱面结果，不是高效算法。显示结果如下图所示：

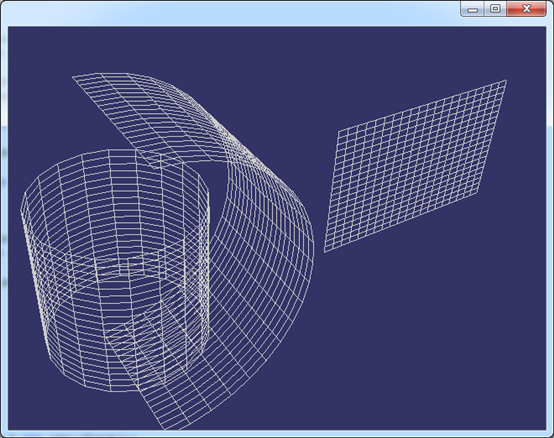
Figure 3.1 General Cylinder for: Circle, Arc, Line

如上图所示分别为对圆、圆弧和直线进行拉伸得到的一般柱面。根据这个原理可以将任意曲线沿给定方向进行拉伸得到一个柱面。

4.Conclusion

通 过对OpenCASCADE中一般柱面的类中代码进行分析可知，OpenCASCADE的这个线性拉伸柱面 Geom_SurfaceOfLinearExtrusion是根据一般柱面的定义实现的，并不是使用NURBS曲面来表示的。当需要用NURBS曲面来 表示一般柱面时，需要注意控制顶点及权值的计算取值。

5. References

1. 赵罡，穆国旺，王拉柱译. 非均匀有理B样条. 清华大学出版社. 2010

2. Les Piegl, Wayne Tiller. The NURBS Book. Springer-Verlag. 1997

3. OpenCASCADE Team, OpenCASCADE BRep Format. 2014

4. Donald Hearn, M. Pauline Baker. Computer Graphics with OpenGL. Prentice Hall. 2009

5. 莫蓉，常智勇. 计算机辅助几何造型技术. 科学出版社. 2009

PDF Version and Source Code: OpenCASCADE Linear Extrusion Surface