FWT [BZOJ 4589:Hard Nim]

4589: Hard Nim

Time Limit: 10 Sec  Memory Limit: 128 MB
Submit: 275  Solved: 152
[Submit][Status][Discuss]

Description

 

 

Claris和NanoApe在玩石子游戏，他们有n堆石子，规则如下：

1. Claris和NanoApe两个人轮流拿石子，Claris先拿。

2. 每次只能从一堆中取若干个，可将一堆全取走，但不可不取，拿到最后1颗石子的人获胜。

不同的初始局面，决定了最终的获胜者，有些局面下先拿的Claris会赢，其余的局面Claris会负。

Claris很好奇，如果这n堆石子满足每堆石子的初始数量是不超过m的质数，而且他们都会按照最优策略玩游戏，那么NanoApe能获胜的局面有多少种。

由于答案可能很大，你只需要给出答案对10^9+7取模的值。

 

 

Input

输入文件包含多组数据，以EOF为结尾。

对于每组数据：

共一行两个正整数n和m。

每组数据有1<=n<=10^9, 2<=m<=50000。

不超过80组数据。

 

Output

 

Sample Input

3 7
4 13

Sample Output

6
120

 

 

其实这题和上午XJOI里的T3差不多。

具体做法请看别人博客http://blog.csdn.net/jr_mz/article/details/51606673

然而 问题来了。第一次我TLE了，交了Mz的代码 发现他只要6s。

然后仔细对比。。。看了好久祝天然的代码。 得出结论【啊首先 只要不开LL就不会TLE。但是时间的瓶颈不在这。】：

　　FWT的数组n(是2的幂、当然)只要大于(注意是严格大于。否则就WA了)其中的任意一个元素就可以。

 

恩。再贴一下各种FWT的公式

xor:

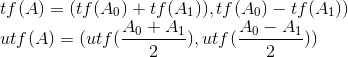
and:

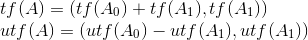
or:

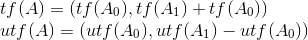
其实公式蛮好推的。。而且也不唯一  比如说 xor  还可以是 A=(A0-A1,A0+A1) 逆A就再反着算一下就可以

还有 FWT只是沿用 FFT和NTT的思想。

【FFT的思想，构造一种可逆的特殊变换trans，使得(trans(a*b))[i]=(trans(a))[i]*(trans(b))[i]。】

但是从界门纲目科属种来看 还是不像FFT与NTT 如此相似。

FWT不需要rev数组 ，举例N=8，下标为0~7。变换的时候，先对01,23,45,67做，再对02,13,46,57做，最后对04,15,26,37做。逆变换把顺序反过来就好了。

而且，这种特殊多项式乘法 满足结合律  ，trans后可以快速幂。

贴本题代码：

 #include <bits/stdc++.h>
 #define LL long long
 const int mo=;
 using namespace std;
 int x,y,n,m,a[],T,t,f[];
 LL po(LL x,LL y){
     LL z=;
     for (;y;y>>=,x=x*x%mo)
     if (y&) z=z*x%mo;
     return z;
 }
 void fwt(int *a,int n,int d){
     for (m=;m<=n;m<<=)
     for (int i=,k=m>>;i<n;i+=m)
     for (int j=i;j<i+k;++j){
         int u=a[j],v=a[j+k];
         a[j]=(u+v)%mo,a[j+k]=(u-v)%mo;
     }
     if (d<){
         LL x=po(n,mo-);
         for (int i=;i<n;++i) a[i]=x*a[i]%mo;
     }
 }//注意a[i]<0
 int main(){
     for (int i=;i<=;++i){
         if (!a[i]) a[++T]=i;
         for (int j=;j<=T;++j){
             int x=a[j]*i; if (x>) break;
             a[x]=; if (!(i%a[j])) break;
         }
     }
     while (scanf("%d%d",&x,&y)==){
         for (t=;a[t]<=y;++t) f[a[t]]=; --t;
         for (n=;n<=a[t];n<<=);
         fwt(f,n,);
         for (int i=;i<n;++i) f[i]=po(f[i],x);
         fwt(f,n,-);
         printf("%d\n",(f[]+mo)%mo);
         for (int i=;i<n;++i) f[i]=;
     }
     return ;
 }

化け物