HDU——2588 GCD

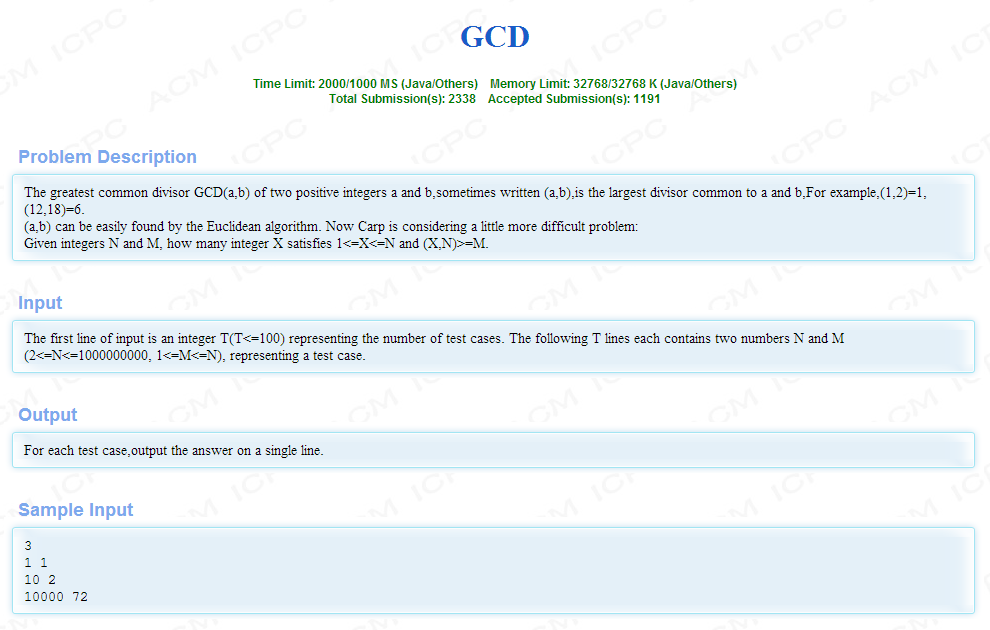
题目大意：

求1~N中与N的最大公约数大于M的个数

思路：

这个题是不是可以想到暴力枚举？？对于每一组数据枚举与他的最大公约数大于m的数的个数。

是，这种做法没错误，但是保准你T成狗。。。。

我们至少要找一个不T的做法吧。。。我们考虑gcd这样一个性质gcd(x,y)=m则gcd（x/m,y/m）=1;我们就可以轻易的发现在这个地方的x/m不就是我们要求的第一个式子中的x吗？？这样我们就只需要统计这样的x/m的个数不就好了吗？！

这样显然就可以知道，这不就是欧拉函数吗？！

是的，那我们就来尝试一下吧。。

代码：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int t,n,m,ans;
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-'; ch=getchar();}
    return x*f;
}
int get_phi(int x)
{
    int sum=x;
    ==)
    {
        ==) x/=;
        sum/=;
    }
    ;i*i<=x;i+=)
    {
        )
        {
            ) x/=i;
            sum=sum/i*(i-);
        }
    }
    ) sum=sum/x*(x-);
    return sum;
}
int main()
{
    t=read();
    while(t--)
    {
        n=read(),m=read();ans=;
        for(int i=m;i<=n;i++)
        {
            )  ans+=get_phi(n/i);
        }
        printf("%d\n",ans);
    }
    return ans;
}

有没有发现这样完美的T成狗了。。。

哈哈，我们在考虑一下别的优化。

跟上一个题一样，我们可以发现能成为他的最大公约数的数是不是一定是她的因子？？我们求它大于m的因子可以暴力枚举能被他整除得数。

好像照样T。。。。

我们想一下上一题我们怎么处理的。我们是不是处理的根n？！ 对于我们处理出来的因子是不是有两个来源，一个是本身i，另一个是n/i？？

这样我们就可以分两种情况来判断，一是i>m，另一种是n/i大于m，这样我们再求n/i的欧拉函数与n/n/i即i的欧拉函数就好了。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int t,n,m,ans;
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-'; ch=getchar();}
    return x*f;
}
int get_phi(int x)
{
    int sum=x;
    ==)
    {
        ==) x/=;
        sum/=;
    }
    ;i*i<=x;i+=)
    {
        )
        {
            ) x/=i;
            sum=sum/i*(i-);
        }
    }
    ) sum=sum/x*(x-);
    return sum;
}
int main()
{
    t=read();
    while(t--)
    {
        n=read(),m=read();ans=;
        ;i*i<=n;i++)
        {
            )
            {
               if(i>=m&&i*i!=n) ans+=get_phi(n/i);
               if(n/i>=m) ans+=get_phi(i);
            }
        }
        printf("%d\n",ans);
    }
    return ans;
}