POJ2486 Apple Tree 【树上背包】

一句话题意：一棵树，一共n个点，每个点上有一个权值，求从1出发，走k步，最多能遍历到的权值。可以往回走。

第一（二）道树上背包题，先是看了dalao的题解，改了一点就过样例了。然而....TLE？？？ 改了挺久发现由于多组数据且没有“0 0”的输入，如果不在读入的时候加“~”或“EOF”就会死循环，从而导致TLE。

状态设计：设f[i][j][0/1]为以i为根的子树上，走j步，能得到的最大权值（0/1的表示会在转移方程中描述） 考虑：（此处参考dalao@zubizakeli ,侵删qwq）每个节点在最终答案中的类型：1，不经过；2，经过但不返回；3，经过且返回 （返回的定义是最终的停止节点不位于该节点的子树中） 那么可以进行转移：

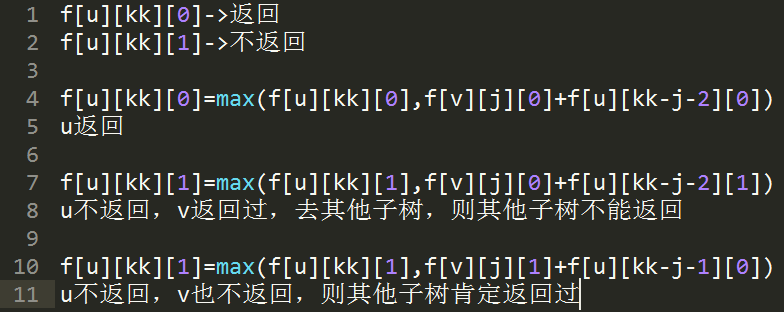
之后便是一些细节问题：给数组赋初值（从0开始！走0步），更新head数组。

实现还是比较简单的啦。

code

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 
 using namespace std;
 
 int n,k,tot;
 int w[],head[];
 int f[][][];
 struct node{
     int to,next,val;
 }edge[];
 
 void add(int x,int y)
 {
     edge[++tot].to=y;
     edge[tot].next=head[x];
     head[x]=tot;
 }
 
 void read(int &x)
 {
     x=;
     char ch=getchar();
     bool flag=false;
     while(ch<''||ch>'') flag|=(ch=='-'),ch=getchar();
     while(ch>=''&&ch<='') x=(x<<)+(x<<)+(ch^),ch=getchar();
     x=flag ? -x : x;
 }
 
 void TreeDp(int u,int fa)
 {
     for(int i=;i<=k;i++) f[u][i][]=w[u],f[u][i][]=w[u];
     for(int i=head[u];i;i=edge[i].next)
     {
         int v=edge[i].to;
         if(v==fa) continue;
         TreeDp(v,u);
         for(int kk=k;kk>=;kk--)
         for(int j=;j<=kk;j++)
         {
             if(kk>=j+) f[u][kk][]=max(f[u][kk][],f[v][j][]+f[u][kk-j-][]);
             if(kk>=j+) f[u][kk][]=max(f[u][kk][],f[v][j][]+f[u][kk-j-][]);
             if(kk>=j+) f[u][kk][]=max(f[u][kk][],f[v][j][]+f[u][kk-j-][]);
         }
     }
 }
 
 void init()
 {
     memset(f,,sizeof(f));
     memset(head,,sizeof(head));
     tot=;
 } 
 
 int main()
 {
     while(scanf("%d%d",&n,&k)!=EOF)
     {
         for(int i=;i<=n;i++) read(w[i]);
         for(int i=;i<=n-;i++)
         {
             int x=,y=;
             read(x),read(y);
             add(x,y),add(y,x);
         }
         TreeDp(,-);
         printf("%d\n",max(f[][k][],f[][k][]));
         init();
     }
     return ;
 }

小结：分类讨论常常也是解题重要的突破口呐。