flask上下管理文相关 - 总结

flask上下管理文相关 - 总结

flask上下文管理机制

当用户请求到来之后,flask内部会创建两个对象:
	ctx = ReqeustContext(),内部封装request/sesion
	app_ctx = AppContext(),内部封装app/g
然后会将此对象通过各自的LocalStack对象:
	_request_ctx_stack = LocalStack()
	_app_ctx_stack = LocalStack()
	将各自的对象添加到local中.

Local是一个特殊结构,他可以为每个线程(协程)维护一个空间进行存取数据.
LocalStack的作用是将Local中维护成一个栈.
内部更细节的结构我也研究过:
	storage = {
        1212:{stack:[ctx,]}
	}

	storage = {
        1212:{stack:[app_ctx,]}
	}

视图函数如果想要获取:request/session/app/g,只需要导入即可,导入的本质是去各自storage中获取各自的对象,并调用封装其内部:request/session/app/g. (获取栈顶的数据top)

请求处理完毕,将各自storage中存储的数据进行销毁.

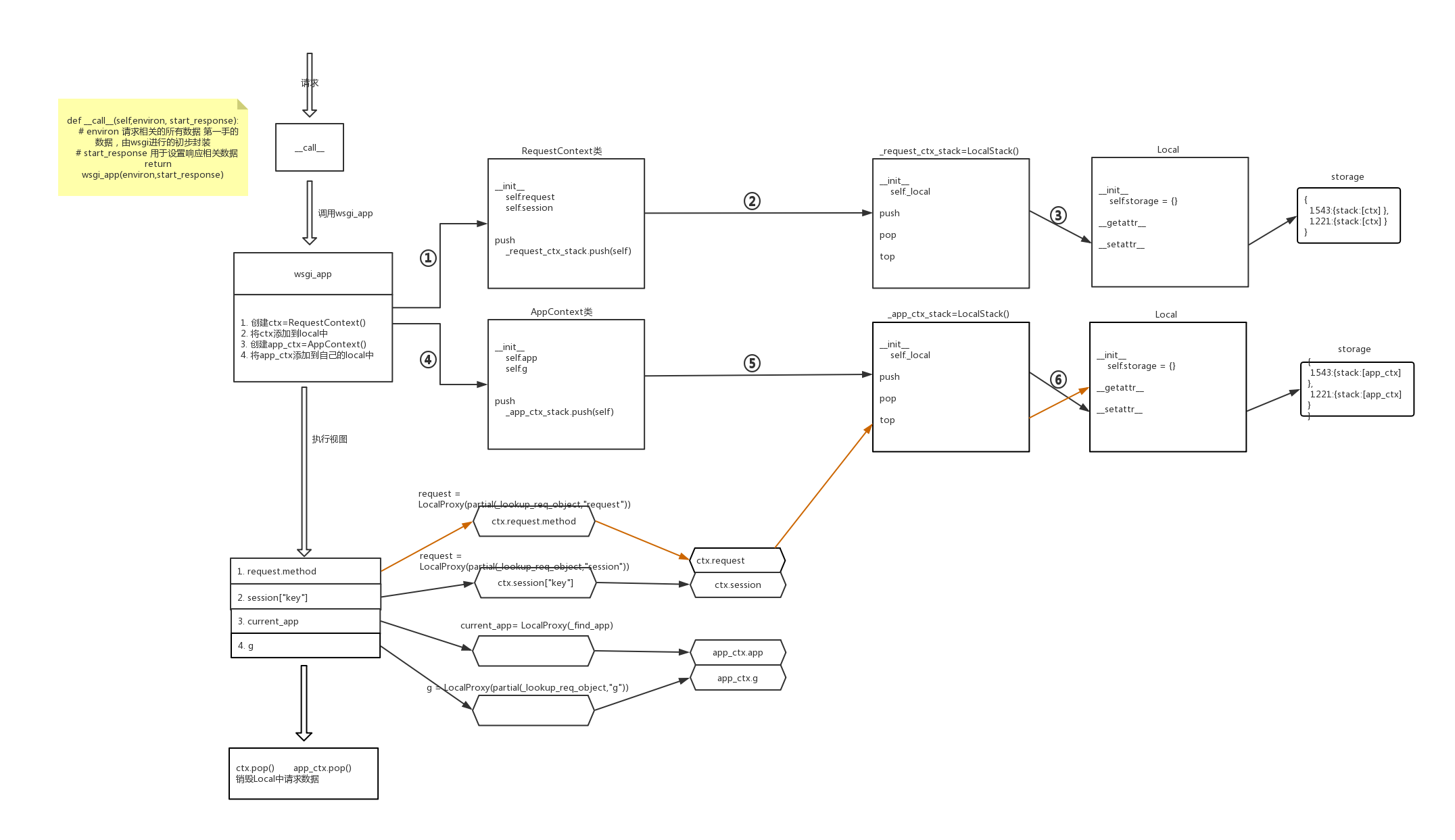
流程图