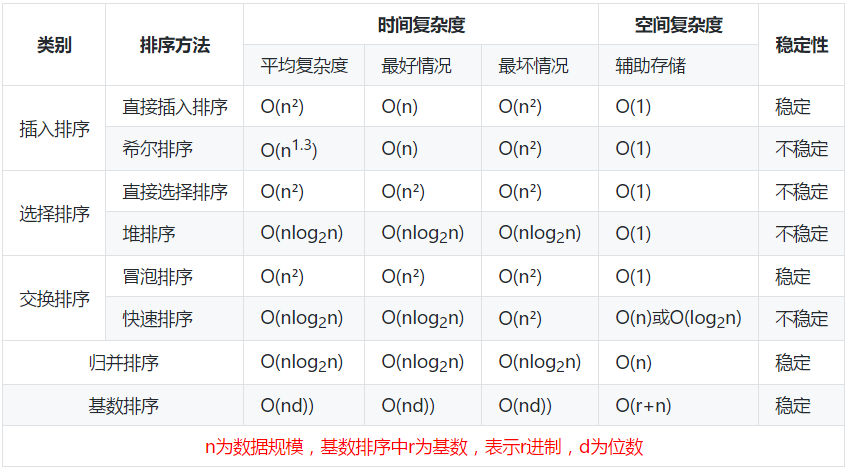
数据结构与算法之排序算法（python实现）

1.冒泡排序

冒泡排序的原理是依次比较相邻的两个数，如果前一个数比后一个数大则交换位置，这样一组比较下来会得到该组最大的那个数，并且已经放置在最后，下一轮用同样的方法可以得到次大的数，并且被放置在正确的位置，最终可以将所有的数放置在正确位置。

例如 56，99，34，10，38，7 这一组数

第一趟比较的过程如下：

，99，34，10，38，7（位置不变）

56，34，99，10，38，7（34与99交换位置）

56，34，10，99，38，7（10与99交换位置）

56，34，10，38，99，7（38与99交换位置）

56，34，10，38，7，99（7与99交换位置）

第一趟比较得到了最大的数99

则第二趟排序的数为56，34，10，38，7

34，56，10，38，7（34与56交换位置）

34，10，56，38，7（10与56交换位置）

34，10，38，56，7（38与56交换位置）

34，10，38，7，（7与56交换位置）

第二趟比较得到了次大的数56

依次类推...

可知一共需要5趟能够排出最终的结果，每趟需要比较的次数也是逐渐递减的（第一趟5次，第二趟4次，第三趟3次。。。）那么一共需要比较（（1+5）*5）/2=15次。如果需要排序的数有n个，那么需要比较n(n-1)/2 次。即时间复杂度为O(n^2)，整个算法只消耗一份数组的空间，所以空间复杂度为O(1)。

另外，排序算法另一个重要的特性稳定性，是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。即假定原数组2个相同的元素a[i]和a[j]，在排序前a[i]在a[j]的前面，那么在排序之后，a[i]仍然在a[j]的前面。冒泡排序是一种稳定排序。

def bubble_sort(alist):
    for j in range(len(alist)-1,0,-1):
        #j表示每次遍历需要比较的次数是逐渐减少的
        for i in range(j):
            if alist[i] > alist[i+1]:
                alist[i],alist[i+1] = alist[i+1],alist[i]
li = [56,99,34,10,38,7]
bubble_sort(li)
print(li)

冒泡排序

2.快速排序

快速排序是从冒泡排序演变而来的算法，但比冒泡排序高效很多。同冒泡排序一样，快速排序也属于交换排序，通过元素之间的比较和交换位置来达到排序的目的。不同的是，冒泡排序在每一轮只把一个元素冒泡到数列的一端，而快速排序在每一轮挑选一个基准元素，并让其他比它大的元素移动到数列一边，比它小的元素移动到数列的另一边，从而把数列拆解成了两个部分。这种方法就叫做分治法。

同样以  12，99，34，10，38，7 这一组数为例子

首先我们需要选取一个基准元素，假设我们选取12为基准元素

7，99，34，10，38，[](从右向左遇到比12小的7放到左边)

，[], 34, 10，38，（从左向右遇到比12大的99放到右边）

7，，34，[]，38，（从右向左遇到比12小的10放到左边）

7，10，[]，34，38，（从左向右遇到比12大的34放到右边）

此时[]左边的数都比12小，[]右边的数都比12大，第一趟排序完成

再对7，10与34，38，39两组数列分别使用快排最终得到正确的排序

快速排序的时间复杂度最好是O(nlog₂n),平均也是O(nlog₂n),最坏情况是序列本来就是有序的，此时时间复杂度为O(n²)，快速排序的空间复杂度可以理解为递归的深度，而递归的实现依靠栈，平均需要递归logn次，所以平均空间复杂度为O(log₂n)。

def quick_sort(alist,start,end):

    #递归退出条件
    if start >= end :
        return
    #设定起始划分元素
    mid = alist[start]

    #low为序列左边的由左向右移动的游标
    low = start
    #high为序列右边从由右向左移动的游标
    high = end
    while low < high:
        while low < high and alist[high] >= mid:
            high -= 1
        #将high指向的元素放到low的位置
        alist[low] = alist[high]
        # 如果low与high未重合，low指向的元素比基准元素小，则low向右移动
        while low < high and alist[low] <= mid:
            low += 1
        #将low指向的元素放到high的位置
        alist[high] = alist[low]

    #退出循环后，low和high重合，此时所指的位置为基准元素的正确位置
    #此时的low和high相等
    alist[low] = mid

    #对基准右边子序列进行快排
    quick_sort(alist,low+1,end)
    #对基准左边子序列进行快排
    quick_sort(alist,start,low-1)

alist = [12,99,34,10,38,7]

quick_sort(alist,0,len(alist)-1)

print(alist)

快速排序

3.插入排序

直接插入排序（straight insertion sort），有时也简称为插入排序（insertion sort），是减治法的一种典型应用。其基本思想如下：

1）对于一个数组A[0,n]的排序问题，假设认为数组在A[0,n-1]排序的问题已经解决了。

2）考虑A[n]的值，从右向左扫描有序数组A[0,n-1]，直到第一个小于等于A[n]的元素，将A[n]插在这个元素的后面。

直接插入排序对于最坏情况（严格递减的数组），需要比较和移位的次数为n(n-1)/2；对于最好的情况（严格递增的数组），需要比较的次数是n-1，需要移位的次数是0。直接插入排序的时间复杂度是O(n^2)，空间复杂度是O(1)，同时也是稳定排序。

用 56，99，34，10，38，7 这一组数来说明一下。

{}，99，34，10，38，7 （插入56）

{56，99}，34，10，38，7（插入99）

{34，56，99}，10，38，7（插入34）

{10，34，56，99}，38，7（插入10）

{10，34，38，56，99}，7（插入38）

{7，10，34，38，56，99}（插入7）

def insert_sort(alist):
    #从第二个位置，下标为1的元素开始向前插入
    for i in range(1,len(alist)):
        #从第i个元素向前比较
        for j in range(i,0,-1):
            if alist[j] < alist[j-1]:
                alist[j],alist[j-1] = alist[j-1],alist[j]

li = [56,99,34,10,38,7]
insert_sort(li)
print(li)

插入排序

4.希尔排序

直接插入排序对于基本有序的数组，会体现出良好的性能，而当数据规模较大且无序的时候，我们就需要用到希尔排序了。

希尔排序的基本思想是把较大的数据集合分割成若干个小组（逻辑上分组），然后对每一个小组分别进行插入排序，此时，插入排序所作用的数据量比较小（每一个小组），插入的效率比较高

用 56，99，34，10，38，7 ，23，45，90，40 这一组数来说明一下。

1.我们首先将步长设置为5

则56，99，34，，38，7 ，23，，90，40 根据步长分成了（56，7），（99，23），（34，45），（10，90），（38，40）5组，

对这5组分别采用插入排序，得到的顺序为（7，56），（23，99），（34，45），（10，90），（38，40）将原始数组调整为7，23，34，10，38，56，99，45，90，40

2.再将步长设置为2

则，23，，10，38，56，，45，90，40 则根据不长将数组分为（7，34，38，99，90），（23，10，56，45，40）两组，两组分别采用插入排序，得到的顺序为（7，34，38，90，99），（10，23，40，45，56）将原始数组调整为7，10，34，23，38，40，90，45，99，56

3，最后将步长设置为1

对7，10，34，23，38，40，90，45，99，56采用插入排序

得到最终排序7，10，23，34，38，40，45，56，90，99

def shell_sort(alist):
    n = len(alist)

    # 初始步长

    gap = int(n / 2)

    while gap > 0:

        # 按步长进行插入排序

        for i in range(gap, n):

            j = i

            # 插入排序

            while j >= gap and alist[j - gap] > alist[j]:
                alist[j - gap], alist[j] = alist[j], alist[j - gap]

                j -= gap

        # 得到新的步长

        gap = int(gap / 2)

alist = [56,99,34,10,38,7 ,23,45,90,40 ]
shell_sort(alist)
print(alist)

希尔排序

5.选择排序

选择排序是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。

用56，99，34，10，38，7 这一组数来说明

1）一开始都未排序：找出其中最小的数7，放到起始位置，即7与56交换位置

，99，34，10，38，56

2）除了第一个位置，剩下的数进行排序：找出最小的数10放到第二个位置，10与99交换

7，10，34，99，38，56

3）第三小的数就是34，不需要交换

4）第四小的数是38，38与99交换

7，10，34，38，99，56

5）第五小的数是56，56与99交换
7，10，34，38，56，99

可以看到选择排序需要比较n(n-1)/2次的，最好、最坏、平均时间复杂度也都为O(n²)，需要一个临时变量用来交换数组内数据位置，所以空间复杂度为O(1)。

def selection_sort(alist):
    n = len(alist)
    for i in range(n-1):
        #需要进行n-1次操作
        #记录最小位置
        min_index = i
        #从i+1位置到末尾选择最小数据
        for j in range(i+1,n):
            if alist[j] < alist[min_index]:
                min_index = j
        #如果此时的值不是在正确的位置
        if min_index != i:
            alist[i], alist[min_index] = alist[min_index], alist[i]

li = [56,99,34,10,38,7]
selection_sort(li)
print(li)

选择排序

6.堆排序

堆排序是基于堆的排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。堆有两种大顶堆和小顶堆。

大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；

小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

堆排序的平均时间复杂度为 Ο(nlogn)。

1.首先，将所有的数字存储在堆中

2.按大顶堆构建堆，其中大顶堆的一个特性是数据将被从大到小取出，将取出的数字按照相反的顺序进行排列，数字就完成了排序

依然用56，99，34，10，38，7 这一组数来说明

第一步：初始堆

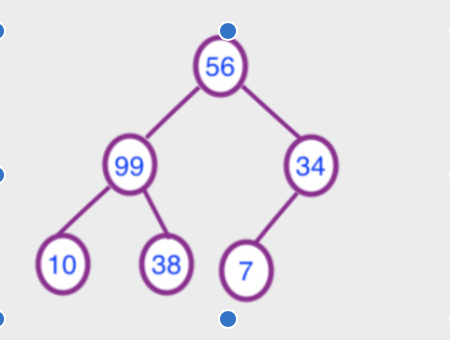
第二步: 初始化大顶堆(从最后一个有子节点开始往上调整最大堆)，每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整)。本案例比较简单，只需要调整一步就得到了大顶堆。

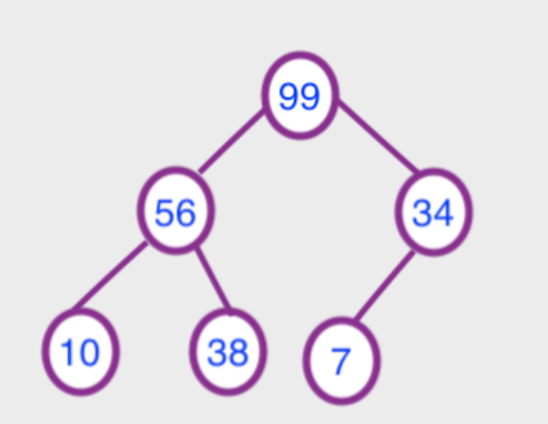
第三步：排序

堆顶元素R[1]与最后一个元素R[n]交换，交换后堆长度减一，可以看到交换后不满足大顶堆的特性，此时7比左子56要小，需要交换，交换之后发现，7比右子38要小，继续交换调整

重复上面的步骤

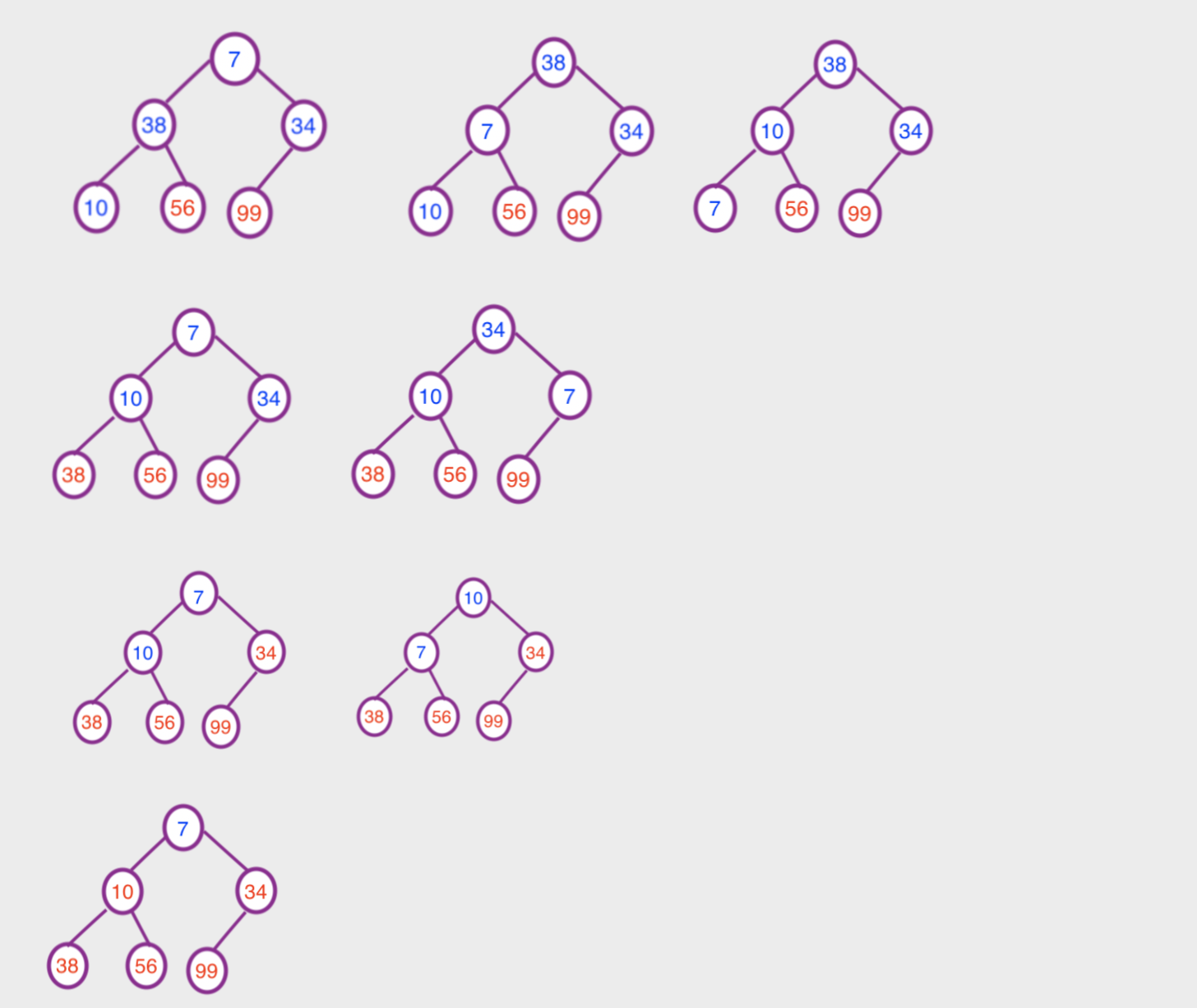
数组的正确顺序应该为7，10，34，38，56，99

def sift_down(arr, node, end):
    root = node

    while True:
        # 从root开始对最大堆调整

        child = 2 * root + 1  # left child
        if child > end:

            break
        print("v:", root, arr[root], child, arr[child])
        print(arr)
        # 找出两个child中交大的一个
        if child + 1 <= end and arr[child] < arr[child + 1]:  # 如果左边小于右边
            child += 1  # 设置右边为大

        if arr[root] < arr[child]:
            # 最大堆小于较大的child, 交换顺序
            arr[root],arr[child] = arr[child],arr[root]
            # 正在调整的节点设置为root
            root = child  #
        else:
            # 无需调整的时候, 退出
            break

    print('-------------')

def heap_sort(arr):
    # 从最后一个有子节点的孩子开始调整最大堆
    first = len(arr)
    for i in range(first, -1, -1):
        sift_down(arr, i, len(arr) - 1)

    print('--------end---', arr)
    # 将最大的放到堆的最后一个, 堆-1, 继续调整排序
    for end in range(len(arr) - 1, 0, -1):
        arr[0], arr[end] = arr[end], arr[0]
        sift_down(arr, 0, end - 1)

def main():

    array = [56, 99,34, 10, 38, 7]
    print(array)
    heap_sort(array)
    print(array)

if __name__ == "__main__":
    main()

堆排序

 

7.归并排序

归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组，再合并数组。

归并排序一共只需要两个步骤：

分：将原数组分为n个子数组，每个子数组长度为1（长度为1的数组自然有序）。

合：依次将两个相邻的有序数组，合并成一个有序数组，重复操作直至剩下一个有序数组。

用56，99，34，10，38，7 这一组数来说明

分：

1）56，99，34 | 10，38，7（将数组一分为二）

2）56| 99，34 | 10，| 38，7 （将数组二分为四）

3）56 | 99 | 34 | 10 | 38 | 7  （将数组分为六个数组）

合：

1）（56，99）（34，10），（38，7）每个数组中的数两两比较得到

（56，99），（10，34），（7，38）

2）将（56，99），（10，34）两个数组进行合并，因为（7，38）落单了暂 不管

对（56，99），（10，34）两个数组进行合并方法，

先各种取最小的值56，10比较，10最小，放入新数组的第一个位置，再将56与34进行比较，34小，放入新数组的第二个位置，得到合并后的数组为（10，34，56，99）

3）将（10，34，56，99）与（7，38）进行比较合并，和上面的方法相同

先各自取出最小值10，7比较，7小，放入新数组的第一个位置，34与38比较，34小，放入第二个位置，56和38比较，38小，放入第三个位置，最终得到的数组为（7，10，34，38，56，99）

def merge_sort(alist):
    if len(alist) <= 1:
        return alist

    # 二分分解
    num = int(len(alist) / 2)
    # 两边分别调用分解
    left = merge_sort(alist[:num])
    right = merge_sort(alist[num:])
    # 合并
    return merge(left, right)

def merge(left, right):
    # 合并操作将两个有序数组left[]和right[]合并成一个有序的大数组
    # left和right的两个下标都是从0开始
    l, r = 0, 0
    result = []
    while l < len(left) and r < len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    # 如果比较到最后剩下的数都是left[]中的，那么直接加上left[]
    result += left[l:]
    # 如果比较到最后剩下的数都是right[]中的，那么直接加上right[]
    result += right[r:]
    return result

alist = [56, 99, 34, 10, 38, 7,3]

sort_alist = merge_sort(alist)

print(sort_alist)

归并排序

8.基数排序

原理请看

https://www.cnblogs.com/duadu/p/6335798.html