[学习笔记] Tangent Distance

Tangent Distance

简介

切空间距离可以用在KNN方法中度量距离，其解决的是图像经过有限变换之后还能否被分类正确，例如。对一张数字为5的手写数字图片，将其膨胀后得到图像p1，此时KNN还应认为p1与原图接近，即距离较近，而不是距离其他类别较近。而Tangent Distance较好的解决了经过图像变换后距离度量的问题，其通过梯度下降算法在切空间中优化求得被分类向量和原始图像及其经过变换后图像的空间中最近的点。

Question

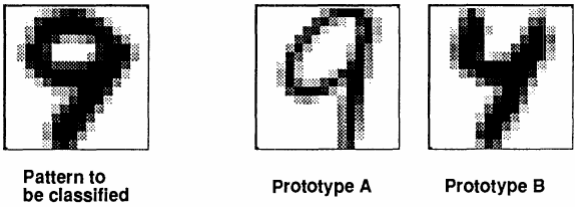
对于上面这张图，我们使用传统的欧式距离，极有可能将左边的图分类成4，而不是9。这暴露出一个问题，传统的欧式距离对旋转、缩放、平移等等变换是不鲁棒的，这就告诉我们我们需要一个新的对于常规变换鲁棒的距离评估标准。

Tangent Vector

切空间向量是如何定义的呢？简单的说，切空间向量的切是指在参数变化方向上的切，即输入图像/向量关于参数的微分。要理解这个，首先我们要先将图像变换数学化(为将问题简单化，我们认为只有一种变换，即旋转变换)：

\[x_{t} = F(x;a)
\]

上式表示输入图像x旋转a角度变为xt，我们怎么求旋转变换关于角度a的微分呢？很简单：

\[T = \lim_{a \to 0}x_t - x = \lim_{a \to 0} F(x;a) - x
\]

这个定义，也就是图像关于a的微分，也就是切空间向量的定义。

那么这个切空间向量有什么用呢，很有用！

我们可以在切线方向也就是切空间里去搜索一种最合适的变换，也就是得到一个最合适的a，使得变换后的图像与原图的欧式距离最小。

一个简单的想法就是穷举出所有的经过变换后的图像，我们将图片每隔1度旋转增广一张，那么肯定能找到一张与所需要分类的图片距离最近的图像。

当然，切空间距离可不是这么简单，上面的想法是让a离散化的想法，实际上a是连续的，我们可以通过梯度下降法来求得一个最为合适的参数a，从而找到最合适的距离。

Tangent Distance

上面我们定义了切空间向量，下面是切空间距离的定义：

\[D_{tan}(x,y) = \min_a [||x + Ta - y||]
\]

这个定义可以这么理解，T由于是参数方向上的微分，乘以系数a然后加上x就是在参数方向上的变换，a取0度，就是不旋转，a取15度就是旋转15度。而a是参数，通过最小化与需要判别图像的欧式距离来得到参数a，继而得到切空间距离。

显然这里优化过程是需要用到梯度下降算法的。

将上式扩展为多种变换，就是对T的定义扩展为矩阵，比如有r种变换，图像像素维度d，则T矩阵就是r x d的。a就是d x 1维度。

Gradient Descent

简答推导一下这里梯度下降的公式：

\[\frac {\partial(||x + Ta - y||)}{\partial a} = \frac{\partial(x + Ta - y)^T(x + Ta - y)}{\partial a}\\ = \frac{\partial}{\partial a}(x^TTa + a^TT^Tx + a^TT^TTa - A^TT^Ty - y^TTa)\\ =2T^Tx + 2T^TTa - 2T^Ty\\ =2T^T(x + Ta - y)
\]

好了，上面推导完了梯度，可以开始写代码了。

Coding

import cv2 as cv
import numpy as np
import copy
class GradientDescent():
    def __init__(self,T):
        self.T = T #(2,784)
    def __call__(self,x,y):
        r,d = self.T.shape # (2,784)
        a = np.ones(shape = (r,1)) # (2,1)
        t = 0
        while True:
            b = copy.copy(a)
            # (784,2).dot (2,1) -> (784,1) -> (2,1)
            a = a - 0.0005 * self.T.dot(x + self.T.T.dot(a) - y)
            t += 1
            #print(a,b)
            if np.sqrt(np.mean((b-a)**2)) < 0.0001 or t > 5000:
                break
        return a,self.T

class TanhDistance():
    def __init__(self,frame,transforms = None):
        self.vectors = []
        h,w = frame.shape
        self.hw = h*w
        if transforms is not None:
            for transform in transforms:
                t = transform(frame) # (h,w)
                self.vectors.append(np.reshape(t,(h*w,)) - np.reshape(frame,(h*w,)))
        self.gradientDescent = GradientDescent(np.array(self.vectors)) # r,28*28
    def __call__(self,x,y):
        x = np.reshape(x,(self.hw,1))
        y = np.reshape(y,(self.hw,1))
        a,T = self.gradientDescent(x,y) # (28*28,1)

        return np.sqrt(np.mean((x + T.T.dot(a) - y)**2))
def get_transforms(frame):
    h,w = frame.shape
    transformations = []
    # rotate
    delta_theta = 5
    M = cv.getRotationMatrix2D(((w-1)/2.0,(h-1)/2.0),delta_theta,1)
    transformations.append(lambda x:cv.warpAffine(x,M,(w,h)))

    # shift
    delta_x = 2
    delta_y = 0
    M = np.float32([[1,0,delta_x],[0,1,delta_y]])
    transformations.append(lambda x:cv.warpAffine(x,M,(w,h)))

    return transformations

if __name__ == "__main__":
    img = cv.imread("/home/xueaoru/图片/0000.jpg")
    gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
    gray = cv.resize(gray,(28,28))/255
    transforms = get_transforms(gray)
    metric = TanhDistance(gray,transforms)

    img2 = cv.imread("/home/xueaoru/图片/000.jpg")
    gray2 = cv.cvtColor(img2,cv.COLOR_BGR2GRAY)
    gray2 = cv.resize(gray2,(28,28))/255 

    print("tan distance:{}".format(metric(gray,gray2)))
    print("l2 distance:{}".format(np.sqrt(np.mean((gray - gray2)**2))))
    #for transform in transforms:
    #    print(transform(gray))

所用图片：

距离结果：

tangent distance:0.3062723225969733

l2 distance:0.336102326896069Q