P2458 [SDOI2006]保安站岗[树形dp]

题目描述

五一来临，某地下超市为了便于疏通和指挥密集的人员和车辆，以免造成超市内的混乱和拥挤，准备临时从外单位调用部分保安来维持交通秩序。

已知整个地下超市的所有通道呈一棵树的形状；某些通道之间可以互相望见。总经理要求所有通道的每个端点（树的顶点）都要有人全天候看守，在不同的通道端点安排保安所需的费用不同。

一个保安一旦站在某个通道的其中一个端点，那么他除了能看守住他所站的那个端点，也能看到这个通道的另一个端点，所以一个保安可能同时能看守住多个端点（树的结点），因此没有必要在每个通道的端点都安排保安。

编程任务：

请你帮助超市经理策划安排，在能看守全部通道端点的前提下，使得花费的经费最少。

输入输出格式

输入格式：

第1行 n，表示树中结点的数目。

第2行至第n+1行，每行描述每个通道端点的信息，依次为：该结点标号i（0<i<=n），在该结点安置保安所需的经费k（<=10000），该边的儿子数m，接下来m个数，分别是这个节点的m个儿子的标号r1，r2，...，rm。

对于一个n（0 < n <= 1500）个结点的树，结点标号在1到n之间，且标号不重复。

输出格式：

最少的经费。

如右图的输入数据示例

输出数据示例：

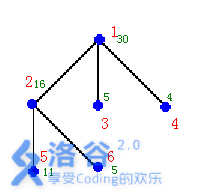
输入输出样例

输入样例#1：

6

1 30 3 2 3 4

2 16 2 5 6

3 5 0

4 4 0

5 11 0

6 5 0

输出样例#1：

说明

样例说明：在结点2，3，4安置3个保安能看守所有的6个结点，需要的经费最小：25

解析：

写完这道题，真的感觉提高了不少！

看到题解写的都是三种状态，虽然我也写了三种状态的解法（比较容易理解），但是咱教练曰：四种状态的也可以。于是便来一发四种状态的（其实本质上也可以化为三种状态，二者无本质区别）。

根据题意，我们得出对于除叶子节点外任意的节点$x$，可以有四种情况：

若$x$的位置的费用为$c_x$，其父节点为$fa$。

$x$的位置没有保安，$fa$的位置有保安
$x$的位置没有保安，$fa$的位置没有保安
$x$的位置有保安，$fa$的位置有保安
$x$的位置有保安，$fa$的位置没有保安

设$dp[x][0/1/2/3]$表示在以$x$为根的子树中，使得每个端点都被覆盖了的最小花费。其中每一种状态对应上面的每一种情况。

注意一下下文提到的状态与情况的区别。

一、

首先考虑$1$情况，对于这样的$x$，假设它任意一个子节点为$y$，那么必然有：

$dp[x][0]=\sum_{y\in tree(x)} min(dp[y][1],dp[y][3])$

即，若要使情况$1$成立，那么必然要从使得它成立的状态（即$y$的父节点没有保安）转移过来。

二、

我们先考虑$3、4$情况，因为他们比较像。。。

我估摸着这个状态是可以合并的，因为无论$x$的$fa$有没有保安，都无所谓，不影响转移。

容易得出：

$dp[x][2/3]=\sum_{y\in{tree(x)}} min(dp[y][0],dp[y][2])+c_x$

即，若要使得情况$3、4$成立，那么$y$的$fa$就要有保安。

三、

这里就比较难理解，但是跟其它题解是同一个思路。

我们首先明确我们对状态的刻画：设$dp[x][0/1/2/3]$表示在以$x$为根的子树中，每个端点都被覆盖了所能得到的最小花费。

对于情况$2$，有两种决策，即

选择从子节点$y$的第$1$种状态转移过来（$dp[y][1]$），这时$y$位置没有保安。
选择从子节点$y$的第$3$种状态转移过来（$dp[y][3]$），这时$y$位置有保安。

可以预见的是，如果对于一个节点$x$，把它作为一个根节点，它的所有子节点$y$都不放置保安时得到最优解（即$x$阶段全部从$dp[y][1]$转移过来），那么显然这样的情况是不符合我们刻画的状态的（根节点$x$未被覆盖到）。

所以我们就要特判一下，一旦出现这种情况，我们就要贪心地去使得当前状态在我们规定的意义下成立。

即，寻找对花费贡献最小的那个$dp[y][3]$，拿它做转移到$x$。

怎么做呢？很简单，我们把最小的$dp[y][3]-dp[y][1]$加进原先我们得出的无法成立的状态中就行了。

证明的话，其实想一想，这个差值其实就是将原先的一个转移$dp[y][1]$变成$dp[y][3]$的时候的变化值。

建议好好品味这道题，能有不错的收获。

参考代码：

#include<iostream>

#include<cstdio>

#include<cstring>

#include<cmath>

#include<algorithm>

#include<string>

#include<cstdlib>

#include<queue>

#include<vector>

#define INF 0x3f3f3f3f

#define PI acos(-1.0)

#define N 2010

#define MOD 2520

#define E 1e-12

#define INF 0x3f3f3f3f

using namespace std;

//start from 1

struct rec{

	int next,ver;

}g[N<<1];

int head[N],tot,n,dp[N][4],a[N];

bool v[N];

inline int read()

{

	int f=1,x=0;char c=getchar();

	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}

	while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}

	return x*f;

}

void add(int x,int y)

{

	g[++tot].ver=y;

	g[tot].next=head[x],head[x]=tot;

}

void calc(int x)

{

	v[x]=1;

	int sum=0,minn=INF;

	dp[x][2]=a[x];dp[x][3]=a[x];

	for(int i=head[x];i;i=g[i].next){

		int y=g[i].ver;

		if(v[y]) continue;

		calc(y);

		//0fa有self没有，1fa没有self没有，2fa有self有，3fa没有self有

		dp[x][2]+=min(dp[y][0],dp[y][2]);

		dp[x][3]+=min(dp[y][0],dp[y][2]);

		if(dp[y][1]>dp[y][3]) sum++;

		else minn=min(minn,dp[y][3]-dp[y][1]);

		dp[x][0]+=min(dp[y][1],dp[y][3]);

		dp[x][1]+=min(dp[y][1],dp[y][3]);

	}

	if(!sum) dp[x][1]+=minn;

}

int main()

{

	n=read();

	for(int i=1;i<=n;i++){

		int ii,k;

		ii=read(),a[ii]=read(),k=read();

		for(int t=1;t<=k;t++){

			int y;

			y=read();

			add(ii,y),add(y,ii);

		}

	}

	calc(1);

	cout<<min(dp[1][1],dp[1][3])<<endl;//根节点不会有父节点嘛，这个好理解

	return 0;

}