【GDOI】2018题目及题解（未写完）

我的游记：https://www.cnblogs.com/huangzihaoal/p/11154228.html

DAY1

题目

T1 农场

【题目描述】

【输入】

第一行，一个整数n。

第二行，n个整数\(a_i\)

【输出】

一个数，最多可以分成几块。

【样例输入】

6

1 1 2 1 2 1

【样例输出】

2

【数据范围限制】

T2 密码锁

【题目描述】

【输入】

输入文件共两行，第一行有两个数字n,m，第二行为一个长为n的数组\(a_1,a_2, ... ,a_n\)

【输出】

输出文件只有一行，表示最少需要的操作次数。答案可能很大，但不会超过\(\sum_i a_i\)，因此不需要对任何数取模。

【样例输入】

Sample Input1

4 3

1 2 1 0

Sample Input2

11 8

1 2 3 4 5 0 5 4 3 2 1

Sample Input3

20 100

30 91 15 72 61 41 10 37 98 41 94 80 26 96 10 88 59 5 84 14

【样例输出】

Sample Output1

2

Sample Output2

8

Sample Output3

313

【数据范围限制】

数据点	数据范围
Case 1-4	\(1\leq n\leq 4,2\leq m\leq 10\)
Case 5-9	\(1\leq n\leq 10^5,2\leq m\leq 3\)
Case 10-15	\(2\leq n,m\leq 3\cdot 10^3\)
Case 16-18	\(2\leq n\leq 2\cdot 10^5\)
Case 1-20	\(1\leq n\leq 10^6,2\leq m\leq 10^9\)

共20个数据点

T3 涛涛接苹果

【题目描述】

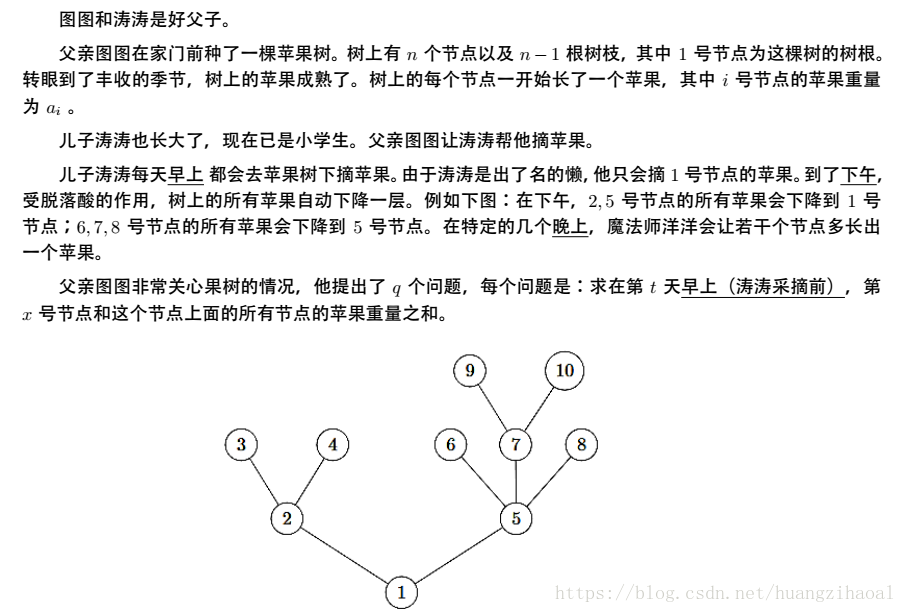
【输入】

【输出】

输出 q 行，每行一个整数表示答案。

【样例输入】

10 5 6

1 2 3 4 5 6 7 8 9 10

9 7

7 10

6 5

7 5

5 8

5 1

2 1

3 2

2 4

2 3 4

2 9 5

1 7 3

4 8 2

5 6 6

2 3

2 5

1 4

3 5

5 1

6 1

【样例输出】

0

43

4

27

11

13

【数据范围限制】

【提示】

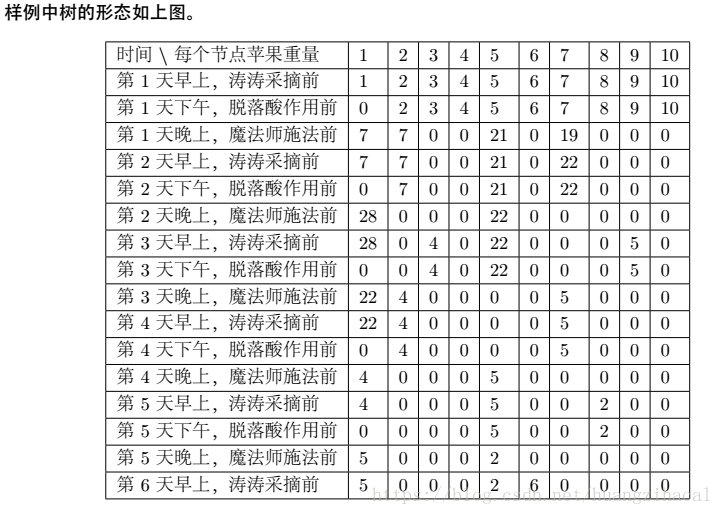
T4 小学生图论题

【题目描述】

【输入】

【输出】

一个整数，表示强连通分量的期望个数。

【样例输入】

Sample Input1

10 2

2 1 3

3 7 8 9

Sample Input2

3 0

【样例输出】

Sample Output1

462789157

Sample Output2

499122179

【数据范围限制】

测试点编号	n	m	\(k_i\)
1、2	\(n\leq 1000\)	0
3、4	\(n\leq 3000\)	\(m\leq 3000\)	\(2\leq k_i\leq n\)
5	\(n\leq 100000\)	\(m\leq 100000\)	\(k_i=2\)
6~10	\(n\leq 100000\)	\(m\leq 100000\)	\(2\leq k_i\leq n\)

---

题解

T1 农场

这题很水，比赛时就有200多人AC了。

题目大意就是给你n个数\(a_1,a_2,...,a_n\)，要求把它们划分成若干份，每一份的和都相等，求出最多能划分成几份。

这题可以用二分+前缀和来做。

输入时顺便求出前缀和数组f，那么\(f_n\)就是\(a_1,a_2,...,a_n\)的和了（最大为\(10^{15}\)）。然后我们就求出它所有小于等于n的因数（可用线性筛法求出）

接下来就枚举所有的因数，设当前枚举到的因数为k，那么我们就判断可不可以将这些数划分成\(\frac{k}{f_n}\)份，如果可以，就用k来更新答案。

判断能否划分的方法很多，下面我就来说二分+前缀和的方法。

弄一个for循环，枚举不大于\(f_n\)的k的倍数i。

然后在f数组内二分查找i，如果没找到，那枚举到的k一定是不行的。

最后输出答案就可以了。

T2 密码锁

这题有一个十分神奇的性质：一个数要么加，要么减，不存在又加又减的情况。

所以可以用差分来做。

设\(f_i\)表示第i个数和第i-1个数的差，那么可以得出\(f_i=(a_i-a_{i-1}+m)\mod m\)

那么对于f值，我们就可以考虑把它+1或-1，由于一个数要么加要么减，所以就可以考虑把它加到m或减到0。

接着就可以发现一定存在一个值mid，使得\(f_{1\space to\space mid}\)全部减到0，\(f_{mid+1\space to\space n}\)全部加到m。

直接枚举就可以了。

然后这题就OK了。

---

标程

T1

#include<cstdio>
using namespace std;
typedef long long ll;
ll s[1000010],a[1000010],ans;
int n,m;
bool b[1000010];
bool failed(ll want)
{
	int l=m,r=n,mid;
	while(l<=r)
	{
		mid=(l+r)/2;
		if(a[mid]==want)
		{
			m=mid+1;
			return 0;
		}
		if(a[mid]>want) r=mid-1;
		else l=mid+1;
	}
	return 1;
}
int main()
{
	freopen("farm.in","r",stdin);
	freopen("farm.out","w",stdout);
	int i,k;ll j;
	scanf("%d",&n);
	for(i=1;i<=n;i++)
	{
		scanf("%lld",&a[i]);
		a[i]+=a[i-1];
	}
	for(i=2;i<=1000000;i++) if(!b[i])
	{
		if(a[n]%i==0) s[++s[0]]=i;
		for(j=(i<<1);j<=1000000;j+=i) if(!b[j])
		{
			b[j]=1;
			if(j<=n&&a[n]%j==0) s[++s[0]]=j;
		}
	}
	for(i=1;i<=s[0];i++)
	{
		m=0;
		for(j=s[i];j<=a[n];j+=s[i])
		{
			if(failed(j)) break;
		}
		if(j>a[n])
		{
			if(a[n]/s[i]>ans) ans=a[n]/s[i];
		}
	}
	printf("%lld\n",ans);
	return 0;
}

T2

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
ll a[1000010],f[1000010],ans,k,last,now;
int main()
{
	freopen("lock.in","r",stdin);
	freopen("lock.out","w",stdout);
	int n,m,i,j;
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++)
	{
		scanf("%lld",&now);
		a[i]=(now-last+m)%m;
		last=now;
	}
	a[n+1]=(m-last)%m;
	sort(a+1,a+n+2);
	for(i=n+1;i>0;i--) f[i]=f[i+1]+m-a[i];
	for(i=0;i<=n+1;i++)
	{
		ans+=a[i];
		if(ans==f[i+1]) break;
	}
	printf("%lld\n",ans);
	return 0;
}

---

DAY2

题目

T1 谈笑风生

【题目描述】

【输入】

【输出】

一行两个数，所需能量P与在能量最小的前提下最短的到达时间t。

【样例输入】

5 7 66

4 3 2 1 5

1 2

1 5

2 3

2 4

2 5

3 4

3 5

【样例输出】

6 64

【数据范围限制】

【样例解释】

从城市1出发，花费6单位能量，依次经过2、4、3、到达首都5，花费32+3+0+29=64秒

T2 滑稽子图

【题目描述】

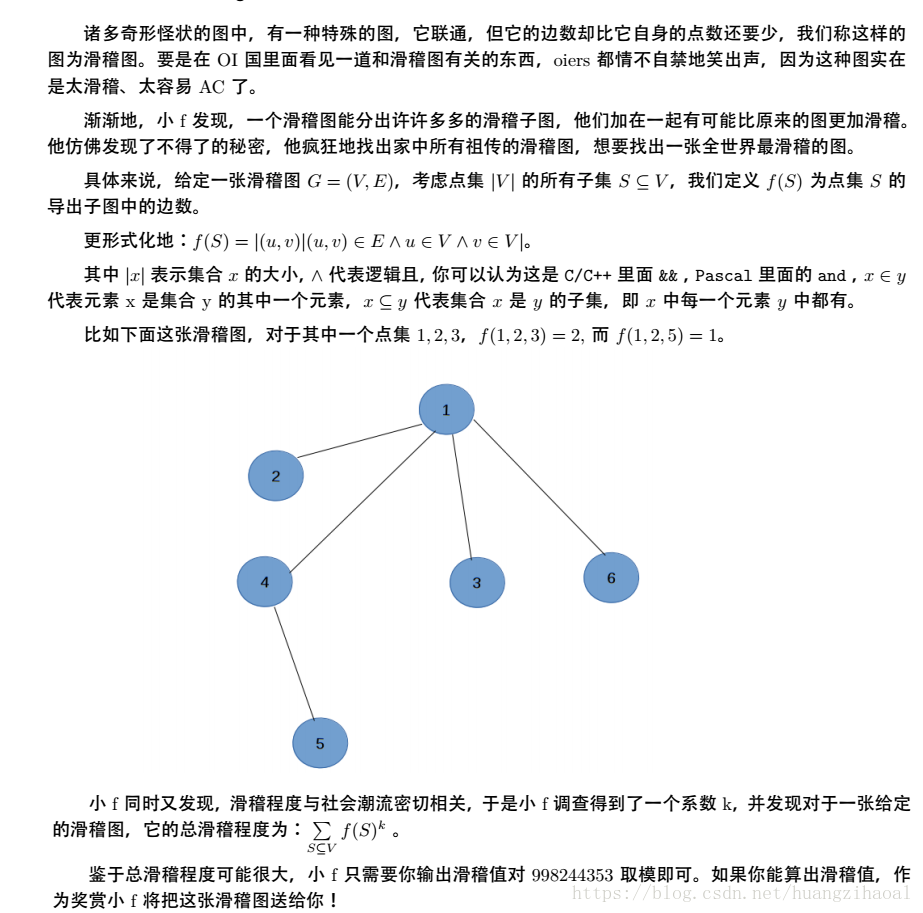
【输入】

【输出】

仅一个整数，表示滑稽值对998244353取模后的值。

【样例输入】

Sample Input1

3 2 1

1 2

1 3

Sample Input2

6 5

1 2

1 3

1 4

1 6

4 5

【样例输出】

Sample Output1

4

Sample Output2

216

【数据范围限制】

数据点	数据限制
Case 1	\(n,m\leq 20\)
Case 2-3	\(n,m\leq 100,k\leq 1\)
Case 4-6	\(n,m\leq 1000,k\leq 2\)
Case 1-13	\(n,m\leq 100000,k\leq 4\)
Case 1-20	\(n,m\leq 100000,k\leq 10\)

共20个测试点。

T3 木板

【题目描述】

【输入】

【输出】

对于每个询问操作，输出一行包含一个整数，代表最大容量。

【样例输入】

4 4

1 2 5 6

1 2 4 2

1 1 2

1 3 4

1 1 4

1 1 3

【样例输出】

1

2

8

6

【数据范围限制】

测试点	N	Q	其他
1	\(\leq 500\)	\(\leq 500\)		\(0\leq x_i\leq 10^9,1\leq h_i\leq 10^9\)
2	\(\leq 10^5\)	\(\leq 10^5\)	询问操作只出现一次	\(0\leq x_i\leq 10^9,1\leq h_i\leq 10^9\)
3	\(\leq 10^5\)	\(\leq 10^5\)	没有修改操作	\(0\leq x_i\leq 10^9,1\leq h_i\leq 10^9\)
4	\(\leq 10^5\)	\(\leq 10^5\)	没有修改操作	\(0\leq x_i\leq 10^9,1\leq h_i\leq 10^9\)
5	\(\leq 10^5\)	\(\leq 10^5\)		\(0\leq x_i\leq 10^9,1\leq h_i\leq 10^9\)
6	\(\leq 10^5\)	\(\leq 10^5\)		\(0\leq x_i\leq 10^9,1\leq h_i\leq 10^9\)
7	\(\leq 10^5\)	\(\leq 10^5\)		\(0\leq x_i\leq 10^9,1\leq h_i\leq 10^9\)
8	\(\leq 5*10^5\)	\(\leq 5*10^5\)		\(0\leq x_i\leq 10^9,1\leq h_i\leq 10^9\)
9	\(\leq 5*10^5\)	\(\leq 5*10^5\)		\(0\leq x_i\leq 10^9,1\leq h_i\leq 10^9\)
10	\(\leq 5*10^5\)	\(\leq 5*10^5\)		\(0\leq x_i\leq 10^9,1\leq h_i\leq 10^9\)

T4 巡逻

【题目描述】

【输入】

【输出】

对于每一次询问，输出一行一个数表示答案，若不存在从这个城市出发的巡逻方案，则输出-1。

【样例输入】

5

-1 1 -1 2 1

1 -1 1 -1 -1

-1 1 -1 3 1

2 -1 3 -1 -1

1 -1 1 -1 -1

3

0 1

1 5

0 1

【样例输出】

4

7

【数据范围限制】

---

题解

T1 谈笑风生

这题真是太变态了！本蒟蒻只拿到了10分。

此题正解：莫比乌斯反演（什么鬼）+二分（答案这么大，不用二分用什么）

不难发现，这题只用先预处理出每条边的权值（即不用能量走过这条边的时间），然后二分答案跑SPFA就可以了。

预处理就是这题的关键所在。

设(u,v)这条边的边权为w(u,v)

暴力的方法就是$$w(u,v)=\sum_{i=1}^{{A_u}\sum_{j=1}}{A_v}((i,j)=1)1$$

但是这样很明显会爆掉。

这是我们就要用莫比乌斯反演了（什么？不知道什么是莫比乌斯反演？自己搜去吧！）

利用这个高大上的方法，我们可以得到以下求法：

\[w(u,v)=\sum_{k=1}^{min(A_u,A_v)}\sum_{i=1}^{\frac{A_u}{k}}\sum_{j=1}^{\frac{A_v}{k}}k\cdot μ_k\cdot(i+j)
\]

---

标程

T1

#include<cstdio>
using namespace std;
#define inf (1e18)+1
int n,num[100010],a[10010],prime[100010],date[50010],first[10010];
bool b[100010],exist[10010];
long long T,anss,dis[10010];
int mymin(int x,int y){return x<y?x:y;}
struct EDGE
{
	int start,end,next;
	long long lenth;
	void count()
	{
		int i,j,k,p,q;
		long long s;
		for(i=mymin(a[start],a[end]);i>0;i--)
		{
			s=i*num[i];p=a[end]/i,q=a[start]/i;
			lenth+=s*q*(1+q)/2*p+s*p*(1+p)/2*q;
		}
	}
}edge[40010];
void Mobius()
{
	int i,j,k;
	num[1]=1;
	for(i=2;i<=100000;i++)
	{
		if(!b[i])
		{
			prime[++prime[0]]=i;
			num[i]=-1;
		}
		for(j=1;j<=prime[0];j++)
		{
			k=i*prime[j];
			if(k>100000) break;
			b[k]=1;
			if(i%prime[j]==0)
			{
				num[k]=0;
				break;
			}
			num[k]=-num[i];
		}
	}
}
bool spfa(long long p)
{
	int head=0,tail=1,u,v,i;
	long long t;
	for(i=2;i<=n;i++) dis[i]=inf;
	date[1]=1;dis[1]=0;
	while(head<tail)
	{
		head++;
		if(head>50000) head=1;
		u=date[head];
		exist[u]=0;
		for(i=first[u];i;i=edge[i].next)
		{
			v=edge[i].end;
			t=edge[i].lenth-p;
			if(t<0) t=0;
			if(dis[u]+t<dis[v])
			{
				dis[v]=dis[u]+t;
				if(!exist[v])
				{
					tail++;
					if(tail>50000) tail=1;
					date[tail]=v;
					exist[v]=1;
				}
			}
		}
	}
	if(dis[n]>T) return 0;
	return 1;
}
int main()
{
	freopen("magic.in","r",stdin);
	freopen("magic.out","w",stdout);
	int m,i,j,k;
	long long l=0,r=inf,mid,ans;
	Mobius();
	scanf("%d%d%lld",&n,&m,&T);
	for(i=1;i<=n;i++) scanf("%d",&a[i]);
	for(k=1;k<=m;k++)
	{
		scanf("%d%d",&i,&j);
		edge[2*k-1]=(EDGE){i,j,first[i],0};
		edge[2*k-1].count();
		first[i]=2*k-1;
		edge[2*k]=(EDGE){j,i,first[j],edge[2*k-1].lenth};
		first[j]=2*k;
	}
	while(l<=r)
	{
		mid=(l+r)/2;
		if(spfa(mid))
		{
			ans=mid;
			anss=dis[n];
			r=mid-1;
		}
		else l=mid+1;
	}
	printf("%lld %lld\n",ans,anss);
	return 0;
}