【LeetCode回溯算法#10】图解N皇后问题（即回溯算法在二维数组中的应用）

N皇后

力扣题目链接(opens new window)

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

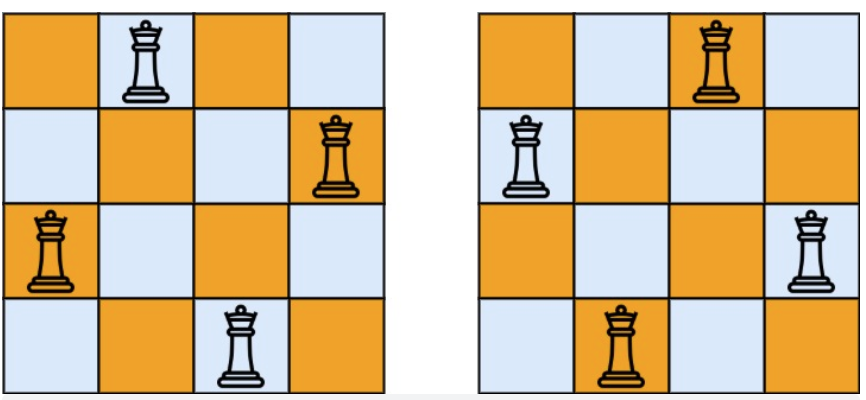
• 输入：n = 4
• 输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
• 解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

• 输入：n = 1
• 输出：[["Q"]]

思路

如何使用回溯方法去搜索一个二维数组？（难点）

其实本题的难点就主要是对于二维数组的操作的不熟练造成的，画个图示先再说：

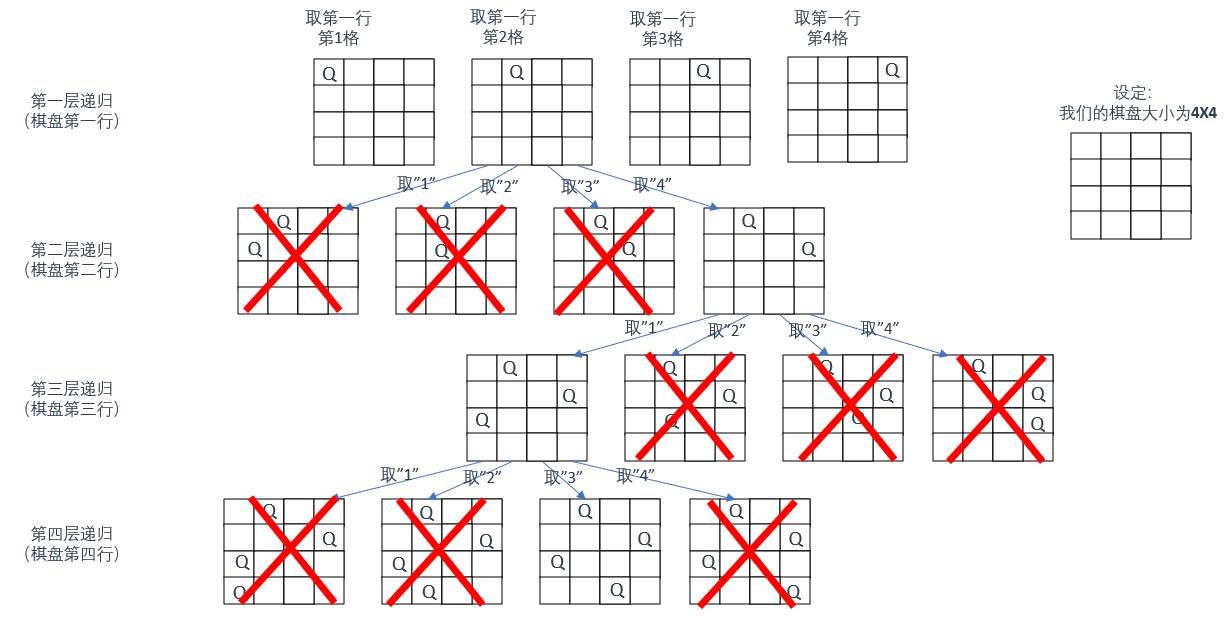
上图展示了在一个 4X4 的棋盘中，其中一种正确摆放结果的获取过程。如图所示，实际上在棋盘（二维数组）中搜索摆放结果时，可以逐层搜索

即：把每层递归看做棋盘中的一层，当前递归处理当前层棋盘的搜索任务

那么棋盘有多大，最后就会触发多少层递归（这里是 4X4 所以有4层递归）

二维矩阵中矩阵的高就是这棵树的高度，矩阵的宽就是树形结构中每一个节点的宽度。当我们遍历到棋盘的最底层时也就到了叶子节点处，此时搜索结束。（结束条件）

代码分析

还是老一套，回溯三部曲

三部曲

1、确定回溯函数的参数以及返回值

看题目给的输出结果得知，我们仍需定义一个二维结果数组res；

输入参数有：棋盘的大小n， 遍历行数记录遍历row以及一维数组chessboard（充当单层棋盘，不要在一开头就定义，因为要每行都清空）

class Solution {
private:
    vector<vector<string>> res;
    void backtracking(int n, int row, vector<string>& chessboard){//确定回溯函数的参数以及返回值

    }

public:
    vector<vector<string>> solveNQueens(int n) {

    }
};

2、确定终止条件

根据上面的讨论，我们希望在遍历到棋盘底部的时候结束

这很好判断，通过row来看即可，row == n就到底了

class Solution {
private:
    vector<vector<string>> res;
    void backtracking(int n, int row, vector<string>& chessboard){//确定回溯函数的参数以及返回值
        //确定终止条件
        if(row == n){//将单层棋盘结果，也就是chessboard，保存至二维结果数组
            res.push_back(chessboard);
            return;
        }
    }

public:
    vector<vector<string>> solveNQueens(int n) {

    }
};

3、确定单层处理逻辑

变量row代表着棋盘的行，也控制着递归的深度

而每层里面的for中的循环变量我们命名为col，其控制着棋盘的列

通过行列变量的配合最终确定皇后的位置

与此同时，在单层处理逻辑中，我们还要加入对N皇后问题规则进行判断的函数isVaild，用以确定当前摆放位置是否合法

class Solution {
private:
    vector<vector<string>> res;
    void backtracking(int n, int row, vector<string>& chessboard){//确定回溯函数的参数以及返回值
        //确定终止条件
        if(row == n){//将单层棋盘结果，也就是chessboard，保存至二维结果数组
            res.push_back(chessboard);
            return;
        }
        //确定单层处理逻辑,每次都从新的列开始搜，因此col初始值是0
        for(int col = 0; col < n; ++col){
            if(isVaild()){
                chessboard[row][col] = 'Q';
                backtracking(n, row + 1, chessboard);
                chessboard[row][col] = '.';//题干中给了用'.'表示空
            }
        }
    }

public:
    vector<vector<string>> solveNQueens(int n) {

    }
};

注意在进入下一层递归时要跳过当前行

规则判断函数isVaild

在N皇后问题中，皇后的摆放规则如下：

• 同一行上不能有两个皇后（不能同行）
• 同一列上不能有两个皇后（不能同列）
• 45度和135度角斜线上不能有两个皇后（不能同斜线）

那么我们只要在isVaild函数中对行、列以及斜线上的皇后情况进行检查就行

那么容易得出，isVaild函数的输入参数是与回溯函数相同的，即int n, int row, vector<string>& chessboard

不过，我们还需要将col也作为参数输入，既然要检查行，行不能不给啊

bool isVaild(int row, int col, vector<string>& chessboard, int n){
    //检查列,就要指定列遍历行
    for(int i = 0; i < row, ++i){
        if(chessboard[i][col] == 'Q') return false;
    }
    //检查45°,以4X4为例，检查以下坐标
    //(0,0)(1,1)(2,2)(3,3)
    for(int i = row - 1, j = col - 1; i >= 0 && j>= 0; --i , --j){
        if(chessboard[i][j] == 'Q') return false;
    }

    //检查135°
    //检查除45°涉及的坐标以外的所有坐标，顺序可能是乱的，但一定都会检查到，不理解子集画一画想一想
    for(int i = row - 1, j = col + 1; i >= 0 && j < n;  --i , ++j){//注意条件，j要++
        if(chessboard[i][j] == 'Q') return false;
    }
    return true;
}

注意事项：

1、这里其实我们不用去检查行（类似检查列的那种操作），因为一层递归for只拿行中的一个数，不会有重

2、关于遍历45度和135度的逻辑，如果实在忘了就自己画个图理解一下

3、实现45度和135度遍历时，我们使用的for的遍历条件是关键，请注意记忆

• 45度时，row和col作为输入肯定越给越大，因此i、j的值每次遍历时都会变大，而遍历条件是 i >= 0 && j>= 0，因此需要--
• 135度时，row和col作为输入也会越给越大，但j的遍历条件是要小于n，因此其要++

（有新理解再补充）

完整代码

class Solution {
private:
    vector<vector<string>> res;
    void backtracking(int n, int row, vector<string>& chessboard){//确定回溯函数的参数以及返回值
        //确定终止条件
        if(row == n){//将单层棋盘结果，也就是chessboard，保存至二维结果数组
            res.push_back(chessboard);
            return;
        }
        //确定单层处理逻辑,每次都从新的列开始搜，因此col初始值是0
        for(int col = 0; col < n; ++col){
            if(isVaild(row, col, chessboard, n)){
                chessboard[row][col] = 'Q';
                backtracking(n, row + 1, chessboard);//注意要跳过当前行
                chessboard[row][col] = '.';//题干中给了用'.'表示空
            }
        }
    }

    bool isVaild(int row, int col, vector<string>& chessboard, int n){
        //检查列,就要指定列遍历行
        for(int i = 0; i < row, ++i){
            if(chessboard[i][col] == 'Q') return false;
        }
        //检查45°,以4X4为例，检查以下坐标
        //(0,0)(1,1)(2,2)(3,3)
        for(int i = row - 1, j = col - 1; i >= 0 && j>= 0; --i , --j){
            if(chessboard[i][j] == 'Q') return false;
        }

        //检查135°
        //检查除45°涉及的坐标以外的所有坐标，顺序可能是乱的，但一定都会检查到，不理解子集画一画想一想
        for(int i = row - 1, j = col + 1; i >= 0 && j < n;  --i , ++j){//注意条件，j要++
            if(chessboard[i][j] == 'Q') return false;
        }
        return true;
	}

public:
    vector<vector<string>> solveNQueens(int n) {
		//定义单行棋盘chessboard
        vector<string> chessboard(n, '.');
        backtracking(n, 0, chessboard);
        return res;
    }
};