我用13行摆烂了你的oj4

13行代码AC oj4是怎么回事呢？13行代码AC oj4相信大家都很熟悉，但是13行代码AC oj4是怎么回事呢，下面就让小编带大家一起了解吧。
13行代码AC oj4，其实就是13行代码AC oj4，大家可能会很惊讶13行代码AC oj4怎么会13行代码AC oj4呢？但事实就是这样，小编也感到非常惊讶。
这就是关于13行代码AC oj4的事情了，大家有什么想法呢，欢迎在评论区告诉小编一起讨论哦！
清华大学电子工程系《数据与算法》课程在线评测系统作业第四题:上班摸鱼算账的会计

（此博客会随着作者的理解加深而逐步修改）

闲话少说，先奉上代码：

#include<cstdio>

int a[200006],t[200006],n;

void add(int x,int k){for(;x<=n;x+=x&-x){t[x]+=k;}}

int sum(int x){int sum=0;for(;x;x-=x&-x)sum+=t[x];return sum;}

int main(){

    scanf("%d",&n);

    for(int i=1;i<=n;i++){scanf("%d",&a[i]);add(i,a[i]);}

    for(int i=1;i<=2*n;i++){

        int boo;scanf("%d",&boo);

        if(boo==1){int x,k;scanf("%d%d",&x,&k);k-=sum(x)-sum(x-1);add(x,k);}

        else{int x,y;scanf("%d%d",&x,&y);printf("%d\n",sum(y)-sum(x-1));}

    }

}

这是一道典型的树状数组模板题。虽然oj提示要求用线段树解决，线段树的题解我会另写一篇博客发出来

原题：

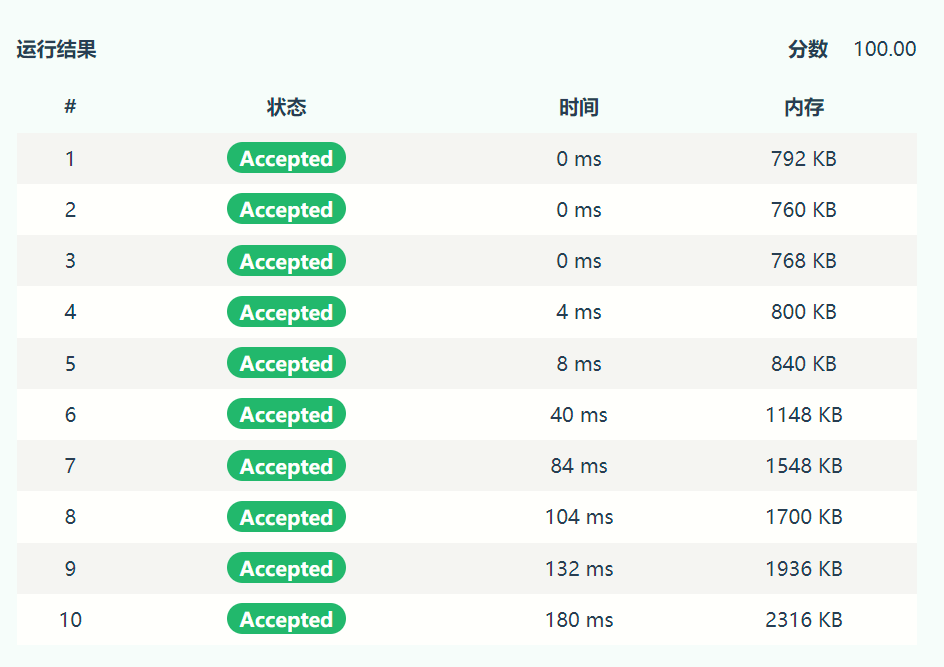
在采用快读之前获得了180ms的坏成绩

首先声明，本人并无oi经验，只是树状数组初学者，正如著名acmer所说：“很多初学者肯定和我一样，只知晓 BIT 代码精炼，语法简明。对于原理好像了解，却又如雾里探花总感觉隔着些什么。”
本人仅在此对与本题有关的树状数组做简要说明，请感兴趣的同学自行学习。

推荐阅读：树状数组（BIT）—— 一篇就够了 - Last_Whisper - 博客园 (cnblogs.com)（哇我和大佬用了同样的博客园主题耶）

用蛮力法完成区间修改与查询的复杂度分析

在学习数据结构之前，在那个不用担心tle的《程序设计基础》年代，我们大家对这道题自然是随手推闭眼写的，即建立一个数组存储各个值，然后用循环暴力方法修改和查询。假设数组长度为n，操作区间长度为m，操作数为k，那么完成这样一套操作的时间复杂度为O(k(n+m))，这自然是题目设计合理，样例难度递进，练习范围全面，提升效果最好的无系数算oj所不能容忍的。我们发现，k次操作的复杂度几乎是不可降低的，对于每一次操作，我们有必要将线性复杂度进一步优化。

树状数组的定义

顾名思义，树状数组是用数组模拟了树的功能。学过线段树的同学可能知道，对于一个区间修改问题，可以用一颗二叉树存储数据的和，从而实现快速修改的操作。

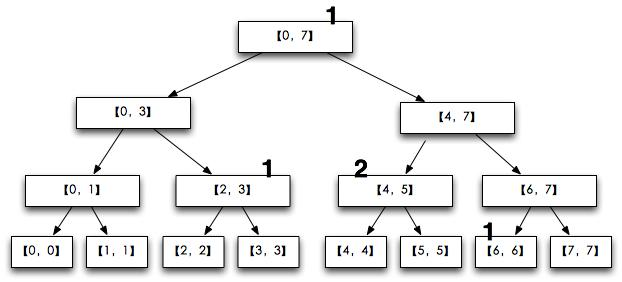
（图片来自网络）

大概原理如上图。通过建立这样一棵树，实现了对于区间部分和的存储。线段树也是解决区间问题的重要手段。
However，本题只要求我们进行单点修改+区间求和，因此我们可以在线段树的基础上更简化一步。
众所周知，和-加数=加数，因此在两个加数与和中，我们只存储其中的两个元素，就可以推出第三个。而在1中的暴力法，我们可以看做存储了两个加数，复杂度表现不佳。线段树则是完全存储了三个数据，在两个数组下标中存储三个数据，显然要进行递归建树等，代码难度较高，且常数较大。我对树状数组的理解是：只存储一个加数以及和，同时通过谨慎地选取，使得每个节点值都是一个特殊区间的和（加数自己的和也是和），再通过巧妙的运算降低复杂度。原理如图。

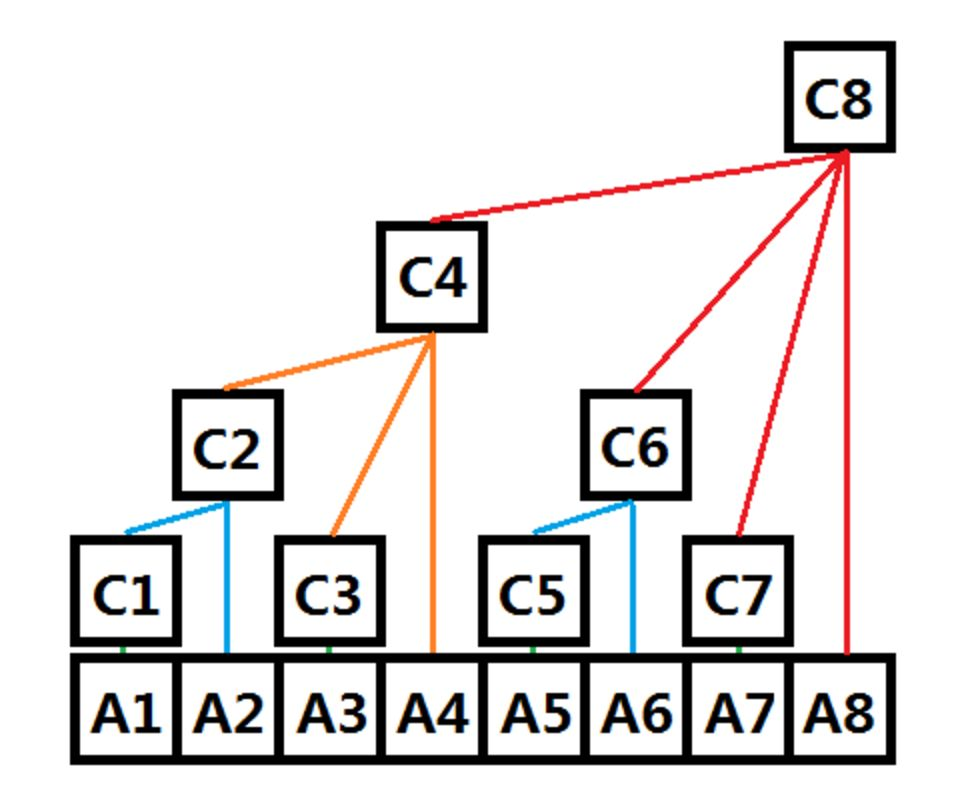
（图片来自网络）

如图所示：

c1=a1,c2=a1+a2,c3=a3,c4=a1+a2+a3+a4,c5=a5,c6=a5+a6,c7=a7,c8=a1+a2+a3+a4+a5+a6+a7+a8。这样便形成了一个树状数组。

树状数组的原理

观察上面的例子，我们发现：
对于每个树状数组（以下记作数组t）节点i，其值t[i] = a[i - 2^k+1] + a[i - 2^k+2] + ... + a[i],其中k为i的二进制中从最低位到高位连续零的长度。下面我们简要证明这一点：
通过前面的分析，我们知道，树状数组节点的选取就是将线段树的所有右儿子去掉取得的，如果我们定义一个量指代从叶子节点开始算起向上的树高度，由于每个右儿子对应一个“2”，也就是对应了一个二进制数位，我们不难发现，数字的二进制最低位到最高位零的长度（称为k）正好是这一高度。比如，对于节点6，其k值为1，它的第一个父节点为上一节点的右儿子，再向上一层则是左儿子。这样，树状数组的各个值我们就构造出来了。
（不难发现指我只能找规律发现，并不会用数学方法证明）
那么，树状数组如何实现区间求和呢？
首先思考从节点1到节点n的求和。我们从n开始入手，Sn=tn+（a1+...+a[n-2^k]）。然后循环往复，令n=n-2^k，一直相加直到n<=0，就得到了所有节点的和。
现在的关键问题是，2^k我们仍然不方便求解啊，用循环的方法的话，最终的复杂度并不能得到保证。
而这，也是树状数组，或者说二进制数的神奇之一。
记lowbit（k）=2^k,则有lowbit(k)=i&(-i)。（i指的是元素下标，由上述定义，我们知道每个i都对应了一个k）下面给出简要证明：
我们设i这个数字的二进制表示中，r1，r2,.....rn数位的值为“1”，其余数位为“0”（定义最后一位为第0位），则有：i=2^r1+....+2^rn。
由上述定义可知，k是i的二进制表示中从最低位到最高位连续0的高度，因此有k=rn。
而由于负数是由补码表示的，对于（-i）,我们知道，由于前面有rn位为0，取反后是1，再+1后让rn个1进位，又第rn+1位是1，取反后是0，进位后得到1，因此得到了第rn+1位是1，后面rn位都是0的数字，也就是说后rn+1位数字与原来数字按位与后的结果都为1，而对于大于rn+1数位的数，由于下面没有进位，因此取反后再按位与的结果都为0。因此最终结果就是在第rn+1位得到一个0。那自然有2^k=i(&-i)成立。
正所谓：“文章本天成，妙手偶得之”。我们不得不为二进制数的精妙而折服。

树状数组的建立，修改与查询。

此处只介绍本题用到的单点修改与区间查询。

树状数组的单点修改

建立树状数组同时也是修改树状数组的一部分。建立树状数组就是把树状数组各个值从0修改到需要值，因此，我们只需要了解如何进行树状数组的单点修改。

void add(int x,int k){for(;x<=n;x+=x&-x){t[x]+=k;}}

从前面的原理分析我们知道，修改一个节点的值，需要对其涉及到的所有值都进行修改。刚才我们在求解t[i]的表达式时，对于每个节点，减去其对应的lowbit得到它需要的作用域（也就是i-2^k+1到i），那么一直递归下去（令i=i-2^k），就可以推到节点1，那么反过来看，我们只要把当前节点一直循环加上lowbit，就可以反推出所有带有这个节点值的节点。

树状数组的区间查询

int sum(int x){int sum=0;for(;x;x-=x&-x)sum+=t[x];return sum;}

我们前面提到了求解1-n区间的和。容易得出，从m到n的求和是Sn-Sm。

彩蛋

某著名oier锐评13行代码：

容我再去优化