matlab拟合函数的三种方法

方法一：多项式拟合polyfit

 1 x=[1 2 3 4 5 6 7 8 9];
 2
 3 y=[9 7 6 3 -1 2 5 7 20];
 4 P= polyfit(x, y, 3)   %三阶多项式拟合
 5
 6 xi=0:.2:10;
 7
 8 yi= polyval(P, xi);  %求对应y值
 9
10 plot(xi,yi,x,y,'r*');

运行结果：

多项式系数：P =0.1481 -1.4030 1.8537 8.2698

使用matlab中的ploy2sym函数：y=poly2sym(P)

得到y=0.1481 * x^3 + -1.4030 * x^2 +1.8537 * x + 8.2698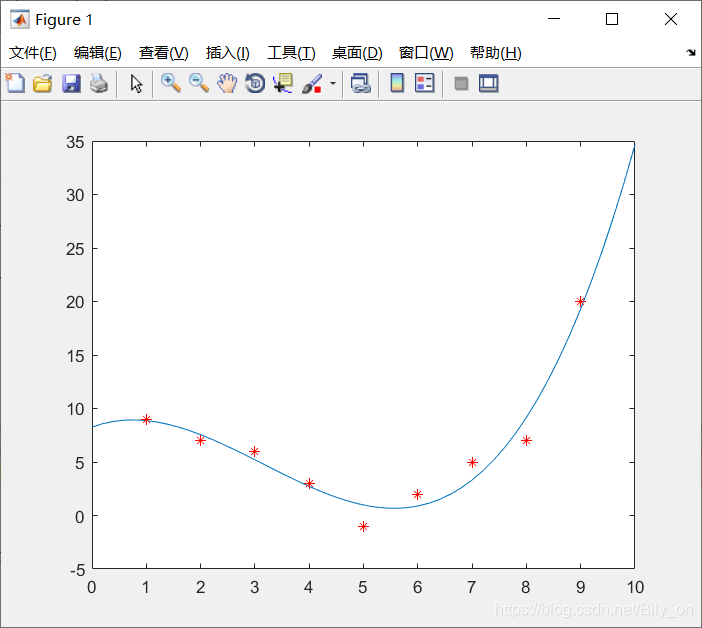

方法二：工具箱拟合cftool

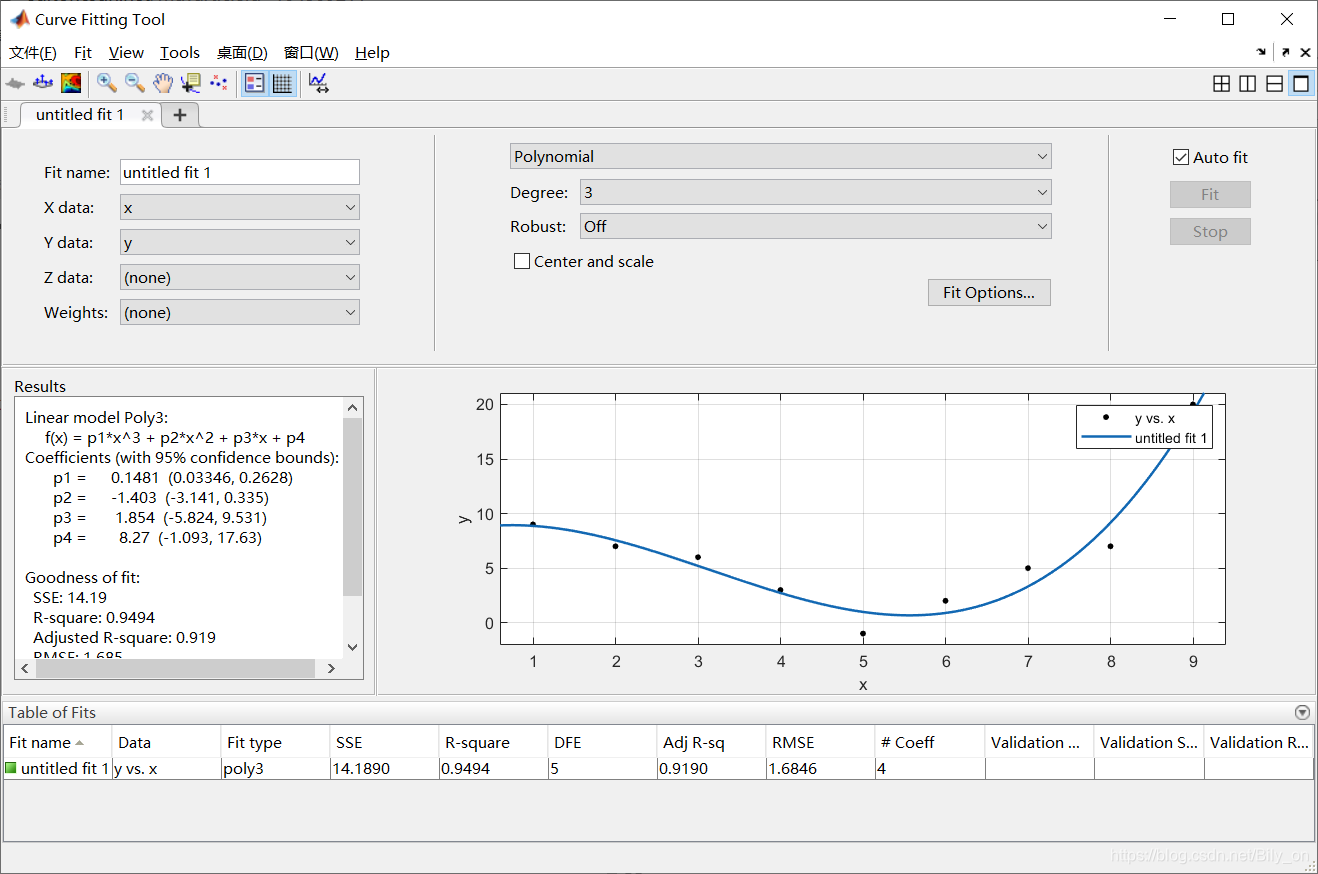
1 x=[1 2 3 4 5 6 7 8 9];
2 y=[9 7 6 3 -1 2 5 7 20];
3
4
5 cftool(x,y)

运行结果：

• 拟合类型中我们选择polynominal（多项式），拟合阶数选择3，运行结果中可见R平方值高达0.94，属于比较准确的.

方法三：指定函数拟合

1、已知数据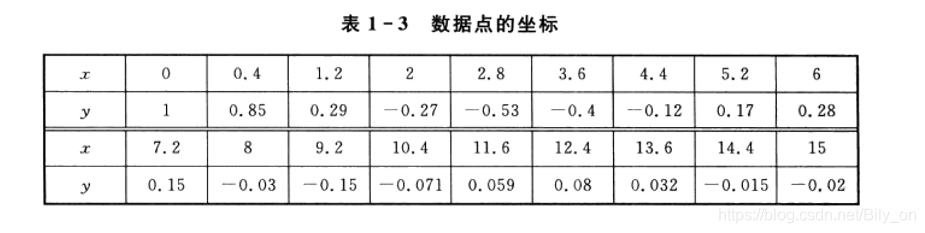
2、作出散点图，观察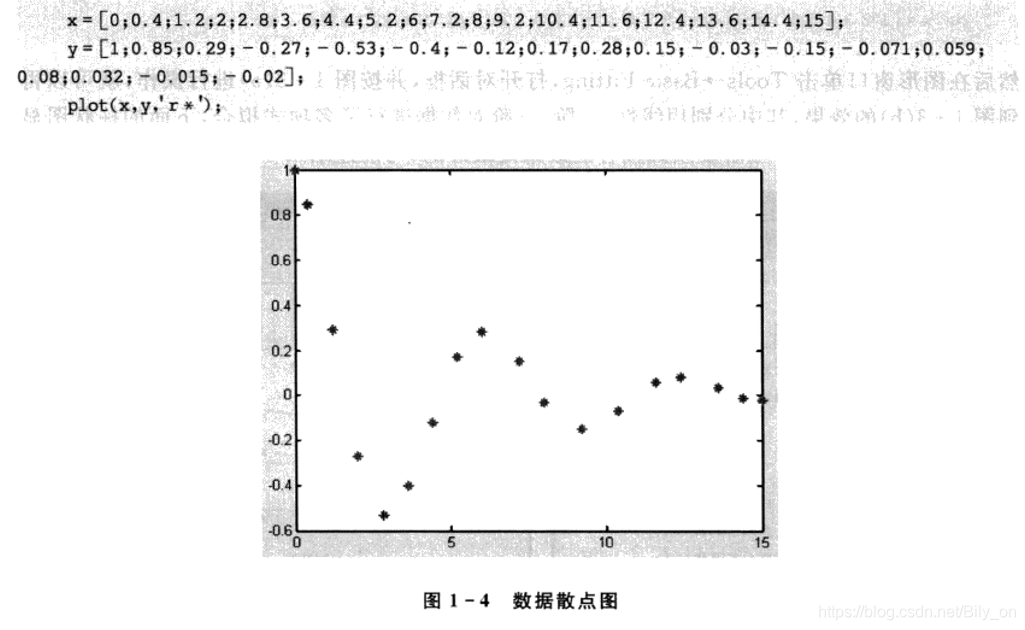

3、拟合

运行结果：

参考文献：matlab在数学建模中的应用 （卓金武）