Java笔记_递归回溯之小老鼠出迷宫问题

递归回溯之小老鼠出迷宫问题

直接看代码

/**
 * @ClassName MiGong01
 * @Description TODO
 * @Author Orange
 * @Date 2021/4/16 8:08
 * @Version 1.0
 **/
public class MiGong01 {
    public static void main(String[] args) {

        int [][] map = new int [10][10];                          //设置迷宫大小
        for(int i = 0; i < map.length; i++) {                     //设置迷宫形状
            for (int j =0; j < map[i].length; j++) {
                map[0][j] = 1;
                map[9][j] = 1;

            }
            map[i][0] = 1;
            map[i][9] = 1;
        }
        map[3][1] = 1;                                            //设置迷宫障碍物的位置
        map[3][2] = 1;
        map[3][3] = 1;
        map[3][4] = 1;
        map[2][4] = 1;
        map[2][5] = 1;
        map[4][6] = 1;
        map[5][5] = 1;
        map[5][6] = 1;
        map[5][7] = 1;
        map[5][8] = 1;
        map[6][4] = 1;
        map[6][5] = 1;
        map[7][4] = 1;

        System.out.println("=====当前地图情况======");
        for(int i = 0; i < map.length; i++) {
            for (int j = 0; j < map[i].length; j++) {
                System.out.print(map[i][j] + " ");               //输出一行
            }
            System.out.println();
        }

        Find F1 = new Find();
        //下右上左
        F1.findWay(map, 1, 1);
        System.out.println("\n==第三种找路的情况如下==");
        for(int i = 0; i < map.length; i++) {
            for(int j = 0; j < map[i].length; j++) {
                System.out.print(map[i][j] + " ");               //输出一行
            }
            System.out.println();
        }
    }
}

class Find {
    //使用递归回溯的思想来解决老鼠出迷宫
    //1. findWay 方法就是专门来找出迷宫的路径
    //2. 如果找到，就返回true ,否则返回false
    //3. map 就是二维数组，即表示迷宫
    //4. i,j 就是老鼠的位置，初始化的位置为(1,1)
    //5. 因为我们是递归的找路，所以我先规定map 数组的各个值的含义
    //   0表示可以走 1表示障碍物 2表示可以走 3表示走过，但是走不通是死路
    //6. 当map[8][8] =2 就说明找到通路,就可以结束，否则就继续找.
    //7. 先确定老鼠找路策略下->右->上->左
    public boolean findWay(int[][] map , int i, int j) {

        if (map[8][8] == 2) {                                     //说明已经找到
            return true;
        } else {
            if (map[i][j] == 0) {                                 //当前这个位置0,说明表示可以走
                //我们假定可以走通
                map[i][j] = 2;
                //使用找路策略，来确定该位置是否真的可以走通
                //下->右->上->左
                if (findWay(map, i + 1, j)) {                   //先走下
                    return true;
                } else if (findWay(map, i, j + 1)) {            //右
                    return true;
                } else if (findWay(map, i - 1, j)) {            //上
                    return true;
                } else if (findWay(map, i, j - 1)) {            //左
                    return true;
                } else {
                    map[i][j] = 3;
                    return false;
                }
            } else {                                            //map[i][j] = 1 , 2, 3
                return false;
            }
        }
    }
    //修改找路策略，看看路径是否有变化
    //下->右->上->左==> 上->右->下->左
    public boolean findWay2(int[][] map , int i, int j) {
        if (map[8][8] == 2) {                                   //说明已经找到
            return true;
        } else {
            if (map[i][j] == 0) {                               //当前这个位置0,说明表示可以走
                //我们假定可以走通
                map[i][j] = 2;
                //使用找路策略，来确定该位置是否真的可以走通
                //上->右->下->左
                if (findWay2(map, i - 1, j)) {                  //先走上
                    return true;
                } else if (findWay2(map, i, j + 1)) {           //右
                    return true;
                } else if (findWay2(map, i + 1, j)) {           //下
                    return true;
                } else if (findWay2(map, i, j - 1)) {           //左
                    return true;
                } else {
                    map[i][j] = 3;
                    return false;
                }
            } else {                                            //map[i][j] = 1 , 2, 3
                return false;
            }
        }
    }

    public boolean findWay3(int[][] map , int i, int j) {

        if (map[8][8] ==2) {                                    //说明已经找到
            return true;
        } else {
            if (map[i][j] == 0) {                               //当前这个位置0,说明表示可以走
                                                                //我们假定可以走通
                map[i][j] = 2;
                                                                //使用找路策略，来确定该位置是否真的可以走通
                                                                //下->左->上->右
                if (findWay3(map, i + 1, j)) {                  //先走下
                    return true;
                } else if (findWay3(map, i, j - 1)) {           //左
                    return true;
                } else if (findWay3(map, i - 1, j)) {           //上
                    return true;
                } else if (findWay3(map, i, j + 1)) {           //右
                    return true;
                } else {
                    map[i][j] = 3;
                    return false;
                }
            } else {                                              //map[i][j] = 1 , 2, 3
                return false;
            }
        }
    }
}

/*程序运行结果：
---------------------
=====当前地图情况======
1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 1 1 0 0 0 1
1 1 1 1 1 0 0 0 0 1
1 0 0 0 0 0 1 0 0 1
1 0 0 0 0 1 1 1 1 1
1 0 0 0 1 1 0 0 0 1
1 0 0 0 1 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 1

==第三种找路的情况如下==
1 1 1 1 1 1 1 1 1 1
1 2 0 2 2 2 2 3 3 1
1 2 2 2 1 1 2 3 3 1
1 1 1 1 1 2 2 3 3 1
1 0 0 0 2 2 1 3 3 1
1 0 0 2 2 1 1 1 1 1
1 0 0 2 1 1 0 0 0 1
1 0 0 2 1 0 0 0 0 1
1 0 0 2 2 2 2 2 2 1
1 1 1 1 1 1 1 1 1 1
--------------------*/

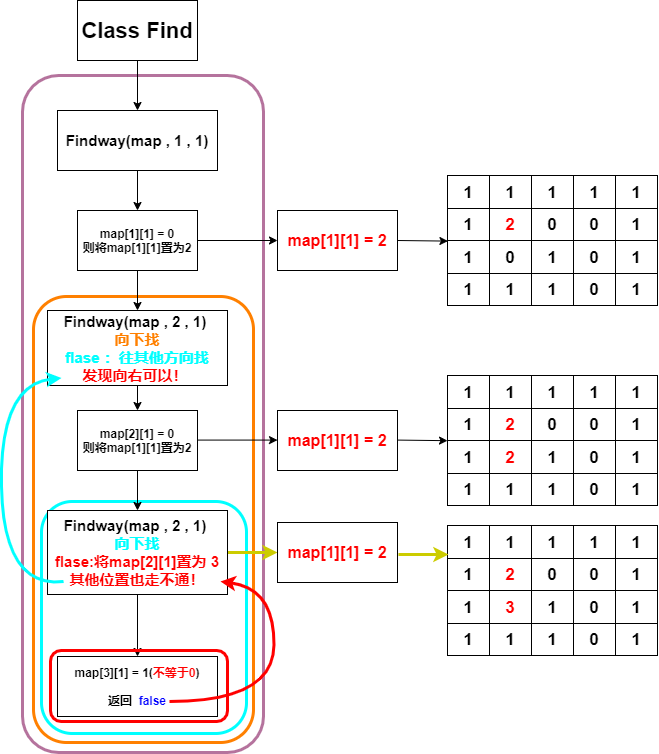
过程分析：

  分析如下图↓