day10 集合——队列（Queue）、Vector & Map集合常用方法 & HashMap的实现原理&二叉树&二叉查找树AVL树&红黑树

集合——List

栈先进后出

队列 先进先出

Queue队列

方法

Queue<Integer> q = new LinkedList<>();

//添加元素
q.add(2);
q.add(3);
q.add(4);

//获取队列长度
int len = q.size();

//获取头元素但不删除，空会引发异常
int ele1 = q.element();
//获取但不删除头元素，空会返回null
int ele2 = q.peek();
//获取并删除头元素
int ele3 = q.poll();

//offer()不超过容量时立即插入元素，超出会返回布尔值false
q.offer(5);
//遍历队列
Integer i = null;//创建的是Integer类型的队列，所以创建int会报错
while((i = q.poll) != null){
    System.out.println(i);
}

Vector

基于动态数组

线程同步（安全），执行效率慢

数据填满会自动填充长度100%，因此ArrayList更节省空间

集合——Map

map中存储的元素是K-V键值对

Map<Integer,String> map = new HashMap<>();

//向map中添加元素
map.put(2,"111");
map.put(2,"222");
map.put(3,"333");

根据键获取值

map中的键是唯一的，对其进行多次赋值，则会对先赋的值进行覆盖

String str = map.get(2);

集合长度

int len = map.size();

获取集合中所有的键的Set集合，再通过该集合对map进行遍历

Set<Integer> set = map.keySet();
for(Integer i: set){
    System.out.println(map.get(i));
}

清空

map.clear();

是否包含指定的key

boolean b = map.containsKey(2);

是否包含指定的value

boolean b1 = map.containsValue("name");

获取所有键值对的Set集合

Set<Entry<Integer,String>> set = map.entrySet();

//size == 0?判断是否为空集合

boolean b1 = map.isEmpty();

根据键删除键值对

map.remove(2);
//根据键值对删除键值对
map.remve(2,"age");

获取所有的value

Collection<String> c = map.values();

替换

map.replace(3,"111");

数据结构

HashMap实现原理

1）HashMap底层数组加链表，java8之后加了红黑树

2）当添加一个元素（Key-value）时,首先计算键值对的key的hash值，以此来确定插入到数组中的位置

3）如果根据hash值确定的数组的位置中已经存在元素，就添加到同一个hash值的后面，于是形成链表

4）当链表长度大于8并且数组中元素（k-v）总数大于64时，链表就转换为红黑树，这样就提高了查找的效率

5）当红黑树中的节点数小于6的时候，红黑树又重新转换为链表

Hash值

HashMap默认初始容量16，扩容*2

扩容因子0.75（占用75%内存的时候就会触发扩容）

默认初始容量=16 每次扩容必须是2的幂

static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

构造函数中未指定时使用的扩容因子。

当一个map中存储的元素个数，超过map容量的75%时，触发扩容

static final float DEFAULT_LOAD_FACTOR = 0.75f;

最大容量，在两个带参数的构造函数中的任何一个隐式指定了更高的值时使用。

static final int MAXIMUM_CAPACITY = 1 << 30;//10,7374,1824

树型阈值，当链表长度等于8时，链表转为红黑树

static final int TREEIFY_THRESHOLD = 8;

非树型阈值，当红黑树中元素个数等于6时，红黑树转为链表

static final int UNTREEIFY_THRESHOLD = 6;

可以树化的最小哈希表容量，当链表长度大于等于8且map中的元素（k-v）个数超过64时，链表就转换为红黑树

static final int MIN_TREEIFY_CAPACITY = 64;

二叉树

1 简介

二叉树（Binary tree）是树形结构的一个重要类型。二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。

二叉树特点是每个结点最多只能有两棵子树，且有左右之分。

二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。

在二叉树中，一个元素也称作一个结点；一个结点拥有子树的数目称为结点的度。

2 定义

二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。

二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。

3 基本形态

二叉树是递归定义的，其结点有左右子树之分，逻辑上二叉树有五种基本形态： 

1)空二叉树——如图1（a）

2)只有一个根结点的二叉树——如图1（b）

3)只有左子树——如图1（c）

4)只有右子树——如图1（d）

5)完全二叉树——如图1（e）

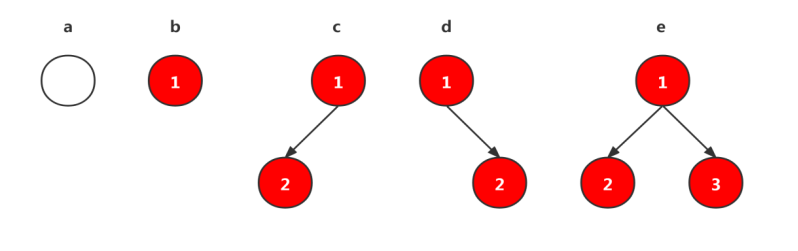
图1

4 特殊类型

满二叉树

一棵深度为k且有2k-1 个结点的二叉树称为满二叉树。

或者说，如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

从满二叉树和完全二叉树的定义可以看出, 满二叉树是完全二叉树的特殊形态, 即如果一棵二叉树是满二叉树, 则它必定是完全二叉树。

5 相关术语

结点 包含一个数据元素及若干指向子树分支的信息

结点的度 一个结点拥有子树的数目

叶子结点 也称为终端结点，没有子树的结点或者度为零的结点

分支结点 也称为非终端结点，度不为零的结点

树的度 树中所有结点的度的最大值

结点的层次 从根结点开始，假设根结点为第1层，根结点的子节点为第2层，依此类推，如果某一个结点位于第L层，则其子节点位于第L+1层

树的深度 也称为树的高度，树中所有结点的层次最大值称为树的深度

有序树 如果树中各棵子树的次序是有先后次序，则称该树为有序树

无序树 如果树中各棵子树的次序没有先后次序，则称该树为无序树

森林 由m（m≥0）棵互不相交的树构成一片森林。如果把一棵非空的树的根结点删除，则该树就变成了一片森林，森林中的树由原来根结点的各棵子树构成

6 二叉树性质

1)二叉树的第i层上至多有2i-1（i≥1）个节点；

2)深度为h的二叉树中至多含有2h-1个节点；

3)若在任意一棵二叉树中，有n0个叶子节点，有n2个度为2的节点，则必有n0=n2+1；

4)具有n个节点的完全二叉树深为log2x+1（其中x表示不大于n的最大整数）[1]

5)若对一棵有n个节点的完全二叉树进行顺序编号（1≤i≤n），那么，对于编号为i（i≥1）的节点：  

当i=1时，该节点为根，它无双亲节点

当i>1时，该节点的双亲节点的编号为i/2

若2i≤n，则有编号为2i的左节点，否则没有左节点

若2i+1≤n，则有编号为2i+1的右节点，否则没有右节点

7 遍历二叉树

遍历是对树的一种最基本的运算，所谓遍历二叉树，就是按一定的规则和顺序走遍二叉树的所有结点，使每一个结点都被访问一次，而且只被访问一次。由于二叉树是非线性结构，因此，树的遍历实质上是将二叉树的各个结点转换成为一个线性序列来表示。

7.1 先序遍历（先根遍历）

遍历顺序：根节点、左子树、右子树

遍历的足迹：沿途经过各结点的“左部”

遍历的结果：A B C D E F G

• A（根）
• B C D（先序根的左子树）
• E F G（先序根的右子树）

7.2 中序遍历（中根遍历）

遍历顺序：左子树、根节点、右子树

遍历的足迹：沿途经过各结点的“下部”

遍历的结果： B D C A F G E

• B D C（中序根的左子树）
• A（根）
• F G E（中序根的右子树）

7.3 后序遍历（后根遍历）

遍历顺序：左子树、右子树、根节点

遍历的足迹：沿途经过各结点的“右部”

遍历的结果： B D C F G E A

• B D C（后序的左子树）
• F G E（后序的右子树）
• A（根）

附录

[1] 对数函数

如果ax =N（a>0，且a≠1），那么数x叫做以a为底N的对数，记作x=logaN，读作以a为底N的对数，其中a叫做对数的底数，N叫做真数。

一般地，函数y=logaX（a>0，且a≠1）叫做对数函数，也就是说以幂（真数）为自变量，指数为因变量，底数为常量的函数，叫对数函数。

二叉查找树

1.1 定义

一棵空树，或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；

（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

（4）没有键值相等的结点。

二叉查找树（Binary Search Tree），又叫：二叉搜索树，二叉排序树。

1.2 查找

步骤：

若根结点的值等于查找的值，成功；

若小于根结点的值，递归查左子树；

若大于根结点的值，递归查右子树；

若子树为空，查找不成功。

1.3 插入

首先执行查找算法，找出被插结点的父亲结点（比较被插入值与结点的值）。

判断被插结点是其父亲结点的左、右儿子。

将被插结点作为叶子结点插入。

若二叉树为空，则首先单独生成根结点。

AVL树（平衡二叉树）

2.1 简介

AVL树是最先发明的自平衡二叉查找树，在AVL树中任何节点的两个子树的高度差的绝对值不超过1，所以它也被称为高度平衡树。

平衡二叉树（Balanced Binary Tree）又被称为AVL树（有别于AVL算法），且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

2.2 定义

AVL树本质上还是一棵二叉查找树，它的特点是：

1.本身首先是一棵二叉查找树。

2.带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。

也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）。

2.3 旋转

旋转的目的：是为了实现在插入新的结点之后，实现二叉树的再平衡。

平衡二叉树有4种旋转方式：

1)单旋转-左旋

2)单旋转-右旋

3)双旋转-左右（先左旋后右旋）

4)双旋转-右左（先右旋后左旋）

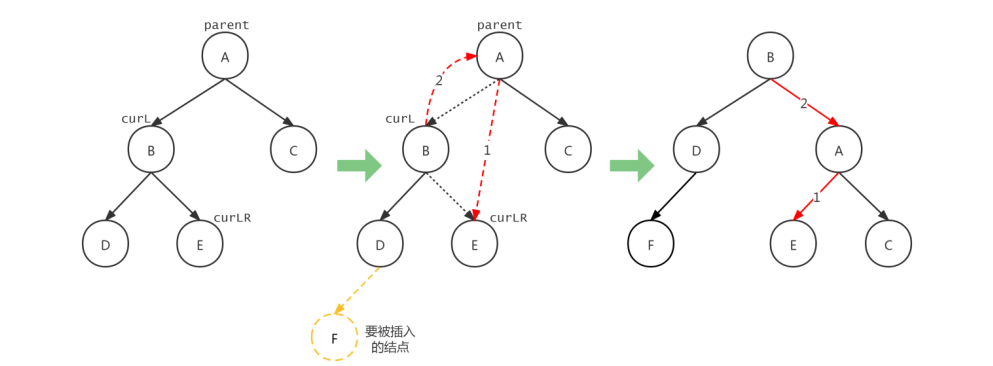
右旋转

修改parent和curLR的孩子指针域

root = parent -> parent

1 修改parent的指针域

parent -> left = curLR

//避免出现左单支的场景

curLR -> parent = parent

2 修改curL的指针域

curL -> right = parent

curL -> parent = root

双旋转-左右

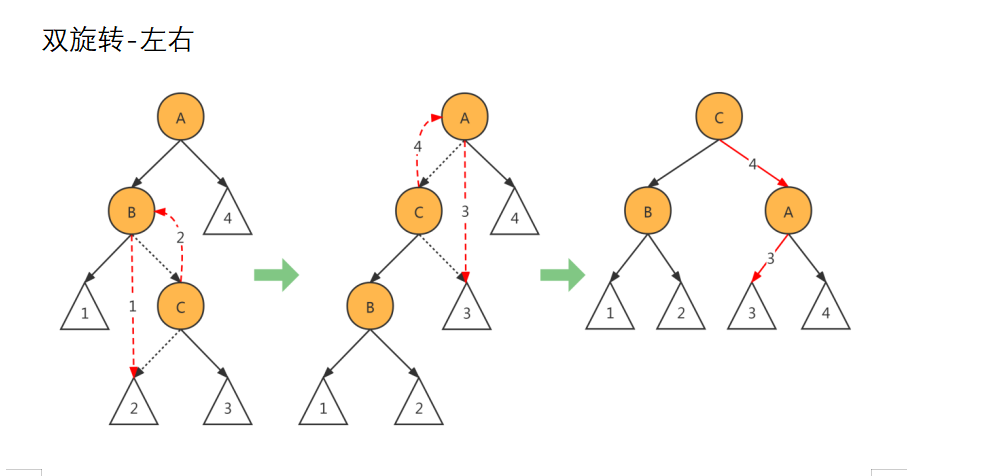
红黑树

红黑树是每个结点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

性质1. 结点是红色或黑色。 

性质2. 根结点是黑色。

性质3. 所有叶子都是黑色。（叶子是NIL结点）

性质4. 每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）

性质5. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。