目标检测算法之Fast R-CNN算法详解

在介绍Fast R-CNN之前我们先介绍一下SPP Net

一、SPP Net

SPP：Spatial Pyramid Pooling（空间金字塔池化）

众所周知，CNN一般都含有卷积部分和全连接部分，其中，卷积层不需要固定尺寸的图像，而全连接层是需要固定大小的输入。

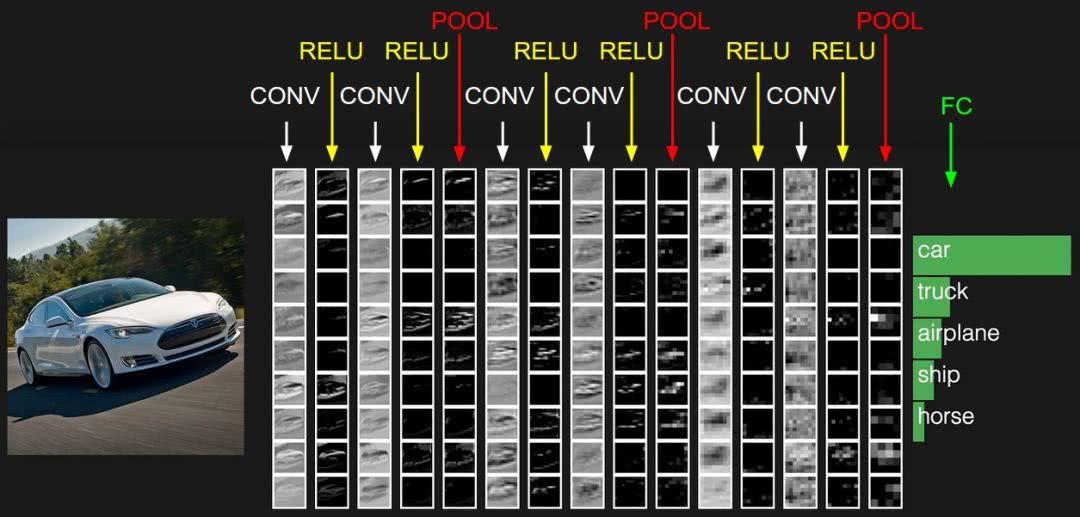
所以当全连接层面对各种尺寸的输入数据时，就需要对输入数据进行crop（crop就是从一个大图扣出网络输入大小的patch，比如227×227），或warp（把一个边界框bounding box的内容resize成227×227）等一系列操作以统一图片的尺寸大小，比如224*224（ImageNet）、32*32(LenNet)、96*96等。

所以，在R-CNN中，才会将每个Region Proposal缩放成（wrap）成统一的227x227并输入到CNN。

但warp/crop这种预处理，导致问题要么被拉伸变形，要么物体不全，限制了识别精确度。换句话说，一张16:9的图片硬是被resize成1:1，你说图片失真不？

二、SPP Net的特点

1. SPP不在限制输入图像的尺度，在最后一个卷积层，接入了金字塔池化，保证传到下一层全连接层的输入固定。

简言之，CNN原本只能固定输入，固定输出，CNN加上SPP之后，便能任意输入、固定输出。

ROI池化层一般跟在卷积层后面，此时网络的输入可以是任意尺度的，在SPP layer中每一个pooling的filter会根据输入调整大小，而SPP的输出是固定维数的向量，然后给到全连接FC层。

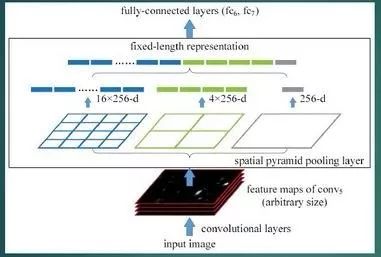
2. 只对原图提取一次卷积特征，得到整张图的卷积特征feature map，然后找到每个候选框在feature map上的映射patch，将次patch作为每个候选框的卷积特征输入到SPP layer和之后的层，完成特征提取工作。节省了大量的时间，比R-CNN有100倍左右的提速

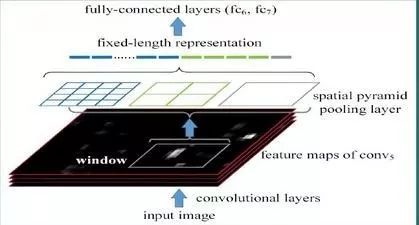
三、Fast R-CNN

Fast R-CNN就是在R-CNN的基础上采纳了SPP Net的方法，使得性能进一步提高。

与R-CNN相比，Fast R-CNN主要有两点不同：一是最后一个卷积层加入了ROI pooling layer，二是损失函数使用了多任务损失函数（multi-task loss），将边框回归Bounding Box Regression直接加入到CNN网络中训练

（1）ROI pooling layer实际上是SPP Net的一个精简版，SPP Net对每个proposal使用了不同大小的金字塔映射，而ROI pooling layer只需要采样到一个7x7的特征图。对于VGG16网络conv5_3有512个特征图，这样所有region proposal对应了一个7*7*512维度的特征向量作为全连接层的输入。也就是说，它可以把不同大小的输入映射到一个固定尺度的特征向量。

（2）R-CNN训练过程分为了三个阶段，而Fast R-CNN直接使用了softmax替代SVM分类，同时利用多任务损失函数边框回归也加入到网络中，整个训练过程就是端到端的（region proposal提取除外）

也就是说，R-CNN的处理流程是先提proposal，然后CNN提取特征，之后用SVM分类器，最后再做box regression。而在Fast R-CNN中，把box regression与region分类合并成multi-task模型，实际实验也证明，这两个任务能够共享卷积特征，并相互促进。

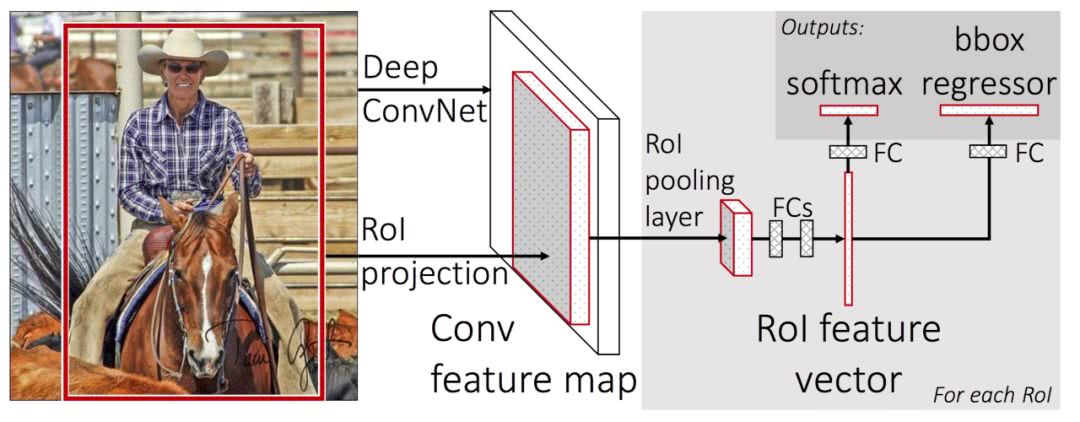
原来的方法：许多候选框（比如2k个）-->CNN-->得到每个候选框的特征-->分类 + 回归

现在的方法：一张完整的图片-->CNN-->得到每个候选框的特征-->分类 + 回归

容易看出，提速的原因在于，不像R-CNN把每个候选区域给深度网络提特征，而是整张图提一次特征，再把候选框映射到conv5上，而SPP只需要计算一次特征，剩下的只需要在conv5层上操作就可以了。

性能上的提升也是明显的：

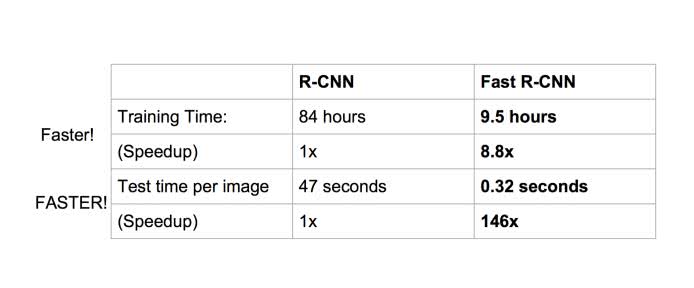
参考地址：

https://cloud.tencent.com/developer/news/281788