Spectral Bounds for Sparse PCA: Exact and Greedy Algorithms[贪婪算法选特征]

概括
Sparse PCA Formulation
算法
代码

概括

这篇论文，不像以往的那些论文，构造优化问题，然后再求解这个问题（一般都是凸化）。而是，直接选择某些特征，自然，不是瞎选的，论文给了一些理论支撑。但是，说实话，对于这个算法，我不敢苟同，我觉得好麻烦的。

Sparse PCA Formulation

非常普遍的问题

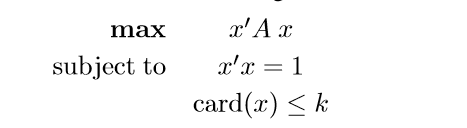
Optimality Conditions

这一小节，论文给出了，上述问题在取得最优的情况下应该符合条件。

条件1

如果\(x^{*} \quad \mathbf{Card}(x^{*})=k\)是上述问题的最优解，那么\(z^{*}\)（由\(x^{*}\)非零元组成）是子举证\(A_k^{*}\)（\(x^{*}\)非零元所在位置，\(A\)的\(k\)行\(k\)列）的主特征向量。

这个条件是显然的。

条件2

感觉和上面也没差啊。

Eigenvalue Bounds

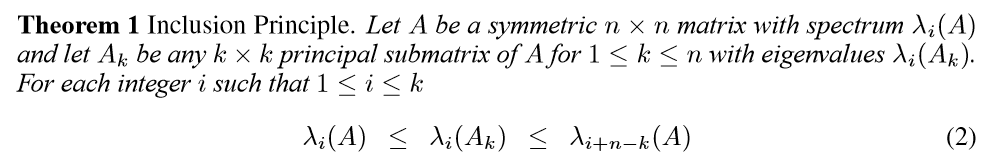
这个定理，可以由一个事实导出：

\(A \in \mathbb{R}^{n\times n}\)为一对称矩阵，\(\lambda_i\)为其特征值，且降序排列。

\(A_{n-1}\)为\(A\)的任意\(n-1\)级主子式，\(\delta_i \quad i=1,2,\ldots,n-1\)为其特征值，那么有下面分隔：

\(\lambda_1 \leq \delta_1 \leq \lambda_2 \leq \ldots \leq \delta_{n-1} \leq \lambda_n\)

根据这个事实，再用归纳法就可以推出上面式子。

分隔定理的证明(《代数特征值问题》p98)

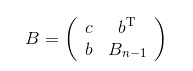
存在正交变换\(Q\),使得\(Q^{\mathrm{T}}BQ\)右下角变为对角阵。若正交矩阵\(S\)使得\(S^{\mathrm{T}}B_{n-1}S\)为对角阵，那么，

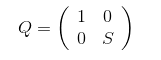
且右下角矩阵的特征值并没有变化。

令：

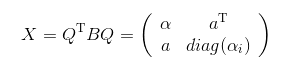
设\(a\)只有\(s\)个成分不为0，若\(a_j=0\),那么\(\alpha_j\)就是\(X\)的特征值。

经过一个适当的置换矩阵\(P\)变换，我们可以得到：

(注意，下面的\(b\)和上面的\(b\)不是一个\(b\),只是为了与书上的符号相一致)

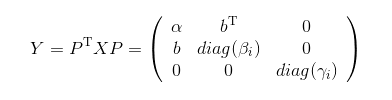
那么只需要考虑

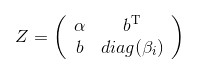
的特征值就行了，因为\(\gamma_i\)是矩阵\(A\)和\(A_{n-1}\)所共有的。

考虑\(Z\)的特征多项式：

\((\alpha-\lambda)\mathop{\prod}\limits_{i=1}^{s}(\beta_i-\lambda)-
\mathop{\sum}\limits_{j=1}^{s}b_j^2\mathop{\prod}\limits_{i \neq j}(\beta_i-\lambda)=0\)

假定\(\beta_i\)中只有\(t\)个不同的值，不失一般性，可令它们为\(\beta_1,\beta_2,\ldots,\beta_t\),

且重数为\(r_1,r_2,\ldots,r_s \quad \mathop{\sum}\limits_{i}r_i=s\)

等式左端有因子:

\(\mathop{\sum}\limits_{i=1}^{t}(\beta_i-\lambda)^{r_i-1}\)

因此，\(\beta_i\)为\(Z\)的特征值，重数为\(r_i-1\)

等式除以\(\mathop{\sum}\limits_{i=1}^{t}(\beta_i-\lambda)^{r_i}\)可得：

\(0=(\alpha-\lambda)-
\mathop{\sum}\limits_{i=1}^{t}c_i^2(\beta_i-\lambda)^{-1}
=a-f(\lambda)\)

\(Z\)的剩余的特征值是\(a-f(\lambda)=0\)的根。

根据正负的特点，和连续函数（实质上是分段的）根的存在性定理，可以知道

\(a-f(\lambda)\)的\(t+1\)个根\(\delta_i\)满足：

\(\delta_1>\beta_1>\delta_2>\ldots>\beta_t>\delta_{t+1}\)

这样所有根的序列就得到了，就是我们要证的。整理一下可以得到，

除了刚刚讲的\(t+1\)个根，

还有\(s-t\)个\(\beta_i\)相同的特征值，以及

\(n-s-1\)个\(\gamma_i\).

另外一个性质

这个性质不想去弄明白了

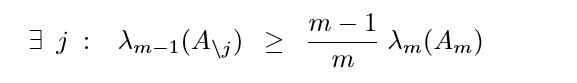
算法

我的理解这样的：

step1.选第一个特征，就是对角元最大的那个

step2.在第一个的基础上，再选一个，这次会形成一个\(2\times2\)的子矩阵，所以，需要选择令这个矩阵首特征值最大的第二个特征。

step3.反复进行，直到k?

这是前向的，还有对应的后向的，一个个减。论文推荐是，俩种都进行，然后挑二者中比较好的一个。

未免太复杂了些？

代码

只写了前向的代码：

import numpy as np

def You_eig_value(C):  #幂法 只输出特征值

    d = C.shape[1]

    x1 = np.random.random(d)

    while True:

        x2 = C @ x1

        x2 = x2 / np.sqrt(x2 @ x2)

        if np.sum(np.abs(x2-x1)) < 0.0001:

            break

        else:

            x1 = x2

    return x1 @ C @ x1

def forward(C):

    n = C.shape[0]

    label1 = set(range(n))

    label = [np.argsort(np.diag(C))[-1]]

    label1 -= set(label)

    count = 0

    while len(label1) > 0:

        count += 1

        maxvalue = 0

        maxi = -1

        for i in label1:

            value = You_eig_value(C[label+[i],:][:,label + [i]])

            if value > maxvalue:

                maxvalue = value

                maxi = i

        label.append(maxi)

        label1 -= {maxi}

    return label

f = open('C:/Users/biiig/Desktop/pitprops.txt')

C = []

for i in f:

    C.append(list(map(float, i.split())))

f.close()

C = np.array(C)

forward(C) # [12, 6, 5, 9, 1, 0, 8, 7, 3, 2, 11, 4, 10]