主席树初步学习笔记（可持久化数组?静态区间第k大?）

我接触 OI也快1年了，然而只写了3篇博客...(而且还是从DP跳到了主席树)，不知道我这个机房吊车尾什么时候才能摸到大佬们的脚后跟orz...

前言：主席树这个东西，可以说是一种非常畸形的数据结构(是线段树畸形程度的两倍)，然而不学又不行，在考试中出现的频率也很高(?)，更重要的是它向我们展示了一个船新的思想——可持久化。

在我学习主席树时，我在网上查了一篇又一篇博客，然而还是感到非常懵逼 0_0 ,这些博客大多由静态区间第k小这一问题来作为学习主席树的切入点，然而……当我学会主席树之后，我才明白区间第k小问题已经是需要在主席树模型上进行拓展的问题了(我还是太弱了...)，而主席树真正的裸题是——可持久化数组！

主席树是什么

让我们从可持久化数组（洛谷P3919）讲起。

主席树就是这么一个数据结构：给你一个序列，支持如下操作：

• 单点修改$ (O(log_2n)) $并生成一个历史版本
• 单点查询$ (O(log_2n)) $并生成一个历史版本
• 访问任何一个历史版本$ (O(1)) $并在此基础上进行其他操作

显然，我们可以开二维数组强行存储每一个历史版本，然而这样时空复杂度都会达到$ O(n^2) $（30分暴力到手美滋滋），进一步分析可以发现，每次只修改一个点，许多点可以重复利用(就像这样)：

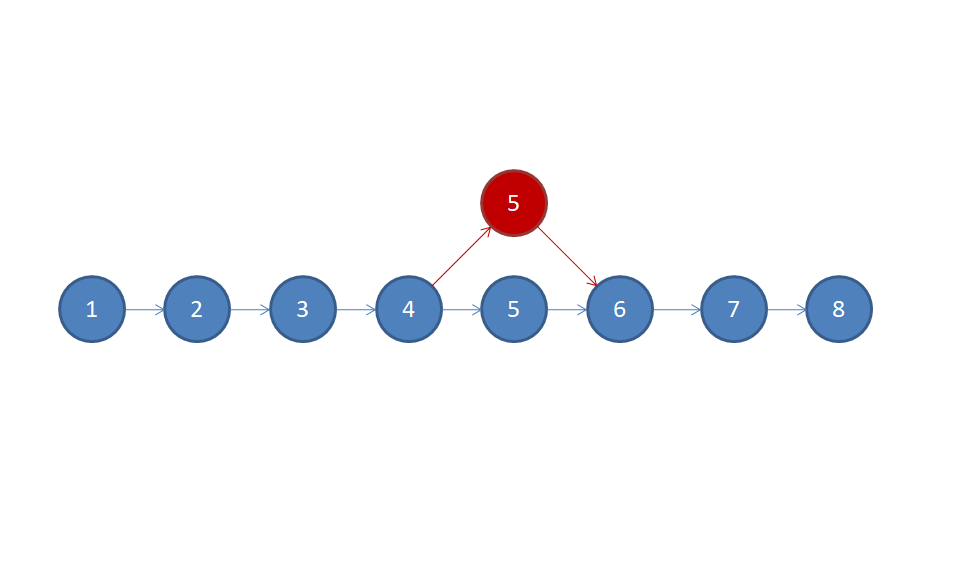
(绘图神器PowerPoint,你值得拥有)

使用了链表结构，修改是 $ O(1) $ 的了，然而查找的复杂度升到了 $ O(n) $ 。至此，你应该想到了——使用二叉树来优化！

主席树的结构

主席树由若干棵线段树构成，每一棵线段树代表一个历史版本。线段树的叶子节点存储原来数组的一个元素，内部节点存储用于查找的信息(比如说，区间的左右端点)与左右儿子的指针。

如图，这是初始版本，对应着4个元素的数组：

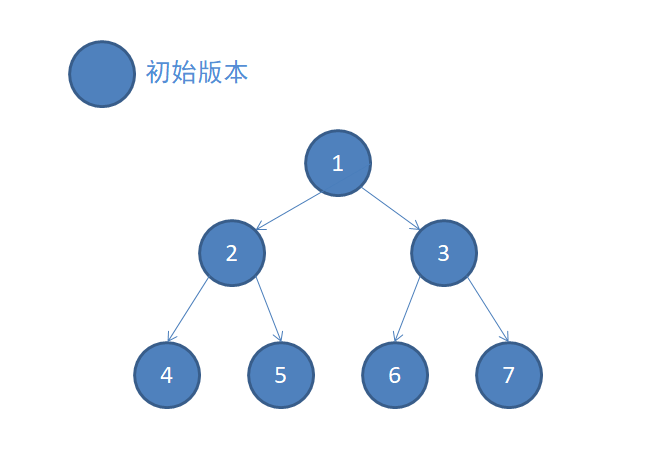
在初始版本上修改数组中的第4个元素(即7号节点)：

在历史版本1上修改数组中的第2个元素(即5号节点)：

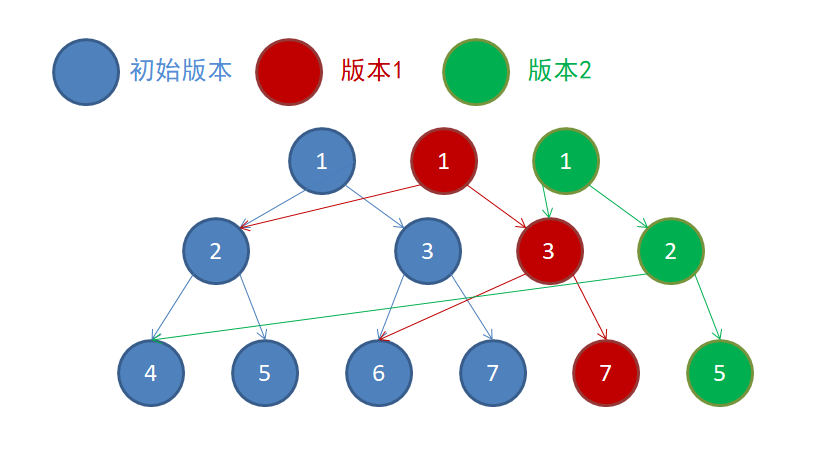
如果觉得上一幅图看不清，让我们去掉多余的节点：

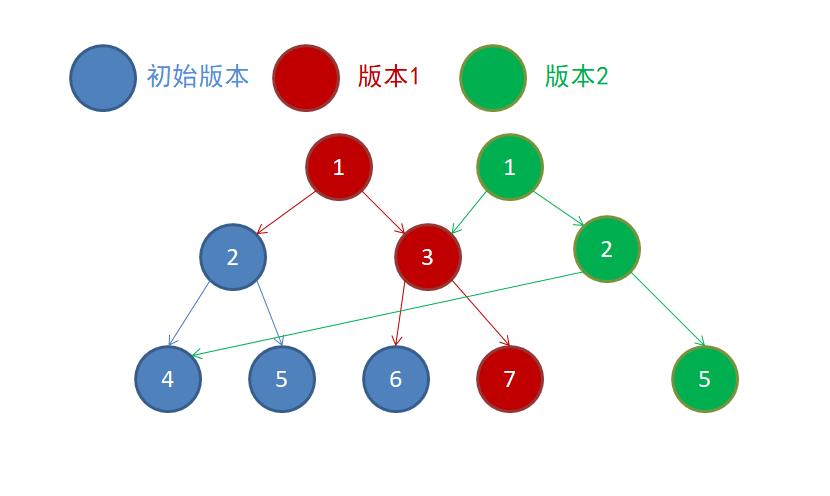
看了这些图，你大概知道主席树是怎么一回事了。每次修改一个叶子节点时，只有这个节点到根节点的路径上的节点会被修改，所以只需要往历史版本中新加入一条链的节点，然后重复的地方指向历史版本就行了。从每个版本的根节点向下遍历就可以得到一个完整的历史版本。(如果还没有看懂，可以结合链表那幅图多看几遍，注意线段树节点的儿子是有左右儿子之分的)

考虑插入链的具体实现。通过观察，我们发现新的节点与历史版本上的这个节点只有两个区别：一是键值被修改(颜色不同)，二是两个儿子指针一个指向历史版本一个指向新版本。所以，我们新建一个节点时，可以先拷贝一份历史版本，然后修改键值与儿子指针。代码如下：

struct CMT_node
{
    int x,l,r;//使用静态内存池和数组模拟指针
}node[MAXN*45];//1e5开40倍,1e6开45倍

void insert(int l,int r,int &x,int y,int tar,int del)
{//l,r为当前区间(用于定位)，tar为目标位置
    x=++cnt;//x引用了上个节点的儿子指针
    node[x]=node[y];//拷贝，y是历史版本
    if(l==r){node[x].x=del;return;}
    int m=(l+r)>>1;
    if(tar<=m)insert(l,m,node[x].l,node[y].l,tar,del);
    else insert(m+1,r,node[x].r,node[y].r,tar,del);
    //向下传递要修改的儿子以及对应的历史版本
}

那么，主席树的基础就这么学习完毕了。

例题

可持久化数组

这个刚刚讲过了啦=w=

//by sclbgw7
#include <cstdio>
#include <cstring>
#include <algorithm>
#define R register
using namespace std;
const int MAXN=1001000;
int a[MAXN],n;

template<class T>void read(T &x)
{
    x=0;int ff=0;char ch=getchar();
    while(ch<'0'||ch>'9'){ff|=(ch=='-');ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=ff?-x:x;
    return;
}

class CMT//ChairMan Tree
{
    private:

    struct CMT_node
    {
        int x,l,r;
    }node[MAXN*45];

    int query(int l,int r,int x,int tar)
    {
        if(l==r)return node[x].x;
        int m=(l+r)>>1;
        if(tar<=m)return query(l,m,node[x].l,tar);
        else return query(m+1,r,node[x].r,tar);
    }

    public:

    int root[MAXN],cnt;

    void build(int l,int r,int &x)
    {
        x=++cnt;
        if(l==r){node[x].x=a[l];return;}
        int m=(l+r)>>1;
        build(l,m,node[x].l);
        build(m+1,r,node[x].r);
    }

    void insert(int l,int r,int &x,int y,int tar,int del)
    {
        x=++cnt,node[x]=node[y];
        if(l==r){node[x].x=del;return;}
        int m=(l+r)>>1;
        if(tar<=m)insert(l,m,node[x].l,node[y].l,tar,del);
        else insert(m+1,r,node[x].r,node[y].r,tar,del);
    }

    int ask(int i,int vi,int x)
    {
        root[i]=++cnt;
        node[root[i]]=node[root[vi]];
        return query(1,n,root[i],x);
    }
}cmt;

int main()
{
    int m;
    read(n),read(m);
    for(R int i=1;i<=n;++i)
      read(a[i]);
    int t1,t2,t3,t4;
    cmt.build(1,n,cmt.root[0]);
    for(R int i=1;i<=m;++i)
    {
        read(t1),read(t2);
        if(t2==1)
        {
            read(t3),read(t4);
            cmt.insert(1,n,cmt.root[i],cmt.root[t1],t3,t4);
        }
        else
        {
            read(t3);
            printf("%d\n",cmt.ask(i,t1,t3));
        }
    }
    return 0;
}

可持久化并查集

有了可持久化数组，那么一切基于数组的数据结构就都可以可持久化啦，不过只能单点修改与查询QvQ

需要注意的几个点：

1. 访问一次主席树的复杂度是 $ O(log_2n) $ 的，而找到祖先需要访问 $ log_2n $ 次，所以一次find()操作的复杂度是$ O(log_2^2n) $的。
2. 由于只能单点修改，所以不能路径压缩，而应该使用按秩合并(也叫启发式合并)来保证复杂度。

一个段子：

(教练看见我在查“并查集启发式合并”)

教练：(突然)启发式合并啊就是blabla...(说了一堆有的没的)，但是一般来说只要用路径压缩就可以了，不需要别的优化

我：emmmm我要搞可持久化

教练：你怎么才学并查集？你不是和他们一起考过并查集吗？

我：我学了并查集啊但是我没有考那次式(因为我是吊车尾进度慢)

教练：你有没有XX学姐总结的并查集资料？

我：没有啊

教练：我发给你

（一会后）教练：这个资料很好的，里面有很多并查集的好题，你不要着急看题解...

我：(一脸懵逼)啊这些题我大概都会...

教练：那你做了可持久化并查集吗？

我：没有啊

教练：那不就是了(带着尴尬+得意的诡异表情离开了)

经过讨论，我们机房一致认为在教练眼里，“可持久化并查集”==“把并查集改一改让它变得可持久化！”，说不定还很纳闷：“XXX学了并查集为什么不把可持久化的一起给学了？...”

忘了贴代码了(洛谷P3402)：

//by sclbgw7
#include <cstdio>
#include <cstring>
#include <algorithm>
#define R register
using namespace std;
const int MAXN=100100;
int n;

template<class T>void read(T &x)
{
    x=0;int ff=0;char ch=getchar();
    while(ch<'0'||ch>'9'){ff|=(ch=='-');ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=ff?-x:x;
    return;
}

class CMT
{
    private:

    int root[MAXN*2],cnt,now;

    struct CMT_node
    {
        int deep,x,l,r;
    }node[MAXN*60];

    void build(int l,int r,int &x)
    {
        x=++cnt;
        if(l==r){node[x].x=l,node[x].deep=1;return;}
        int m=(l+r)>>1;
        build(l,m,node[x].l);
        build(m+1,r,node[x].r);
    }

    void insert(int l,int r,int &x,int y,int tar,int del)
    {
        x=++cnt,node[x]=node[y];
        if(l==r){node[x].x=del;return;}
        int m=(l+r)>>1;
        if(tar<=m)insert(l,m,node[x].l,node[y].l,tar,del);
        else insert(m+1,r,node[x].r,node[y].r,tar,del);
    }

    int query(int l,int r,int x,int tar)
    {
        if(l==r)return x;
        int m=(l+r)>>1;
        if(tar<=m)return query(l,m,node[x].l,tar);
        else return query(m+1,r,node[x].r,tar);
    }

    public:

    void init()
    {
        build(1,n,root[0]);
    }

    void back(int x)
    {
        root[++now]=++cnt;
        node[cnt]=node[root[x]];
    }

    int find(int x)
    {
        int x1,x2=x;
        do
        {
            x1=x2;
            x=query(1,n,root[now],x2);
            x2=node[x].x;
        }
        while(x1!=x2);
        return x;
    }

    void merge(int x,int y)
    {
        x=find(x),y=find(y);
        back(now);
        if(x==y)return;
        if(node[x].deep>node[y].deep)swap(x,y);
        ++node[y].deep;
        insert(1,n,root[now],root[now-1],node[x].x,node[y].x);
    }

    int ask(int x,int y)
    {
        back(now);
        x=find(x),y=find(y);
        if(x==y)return 1;
        return 0;
    }
}cmt;

int main()
{
    int m;
    read(n),read(m);
    cmt.init();
    int t1,t2,t3;
    for(R int i=1;i<=m;++i)
    {
        read(t1),read(t2);
        if(t1==1)
        {
            read(t3);
            cmt.merge(t2,t3);
        }
        else if(t1==2)
          cmt.back(t2);
        else
        {
            read(t3);
            printf("%d\n",cmt.ask(t2,t3));
        }
    }
    return 0;
}

静态区间第k小

啊我已经很累辣QwQ，干脆到时候开一个题解把静态与动态的一起讲了吧...

那么主席树基础就到这里，有什么问题欢迎提出(虽然你看我写博客的频率就大概知道我不怎么能看得到=。=还请谅解)