GeneralizedLinearAlgorithm in Spark MLLib

SparkMllib涉及到的算法

Classification
Linear Support Vector Machines (SVMs)
Logistic regression
Regression
Linear least squares, Lasso, and ridge regression
Streaming linear regression

GeneralizedLinearAlgorithm

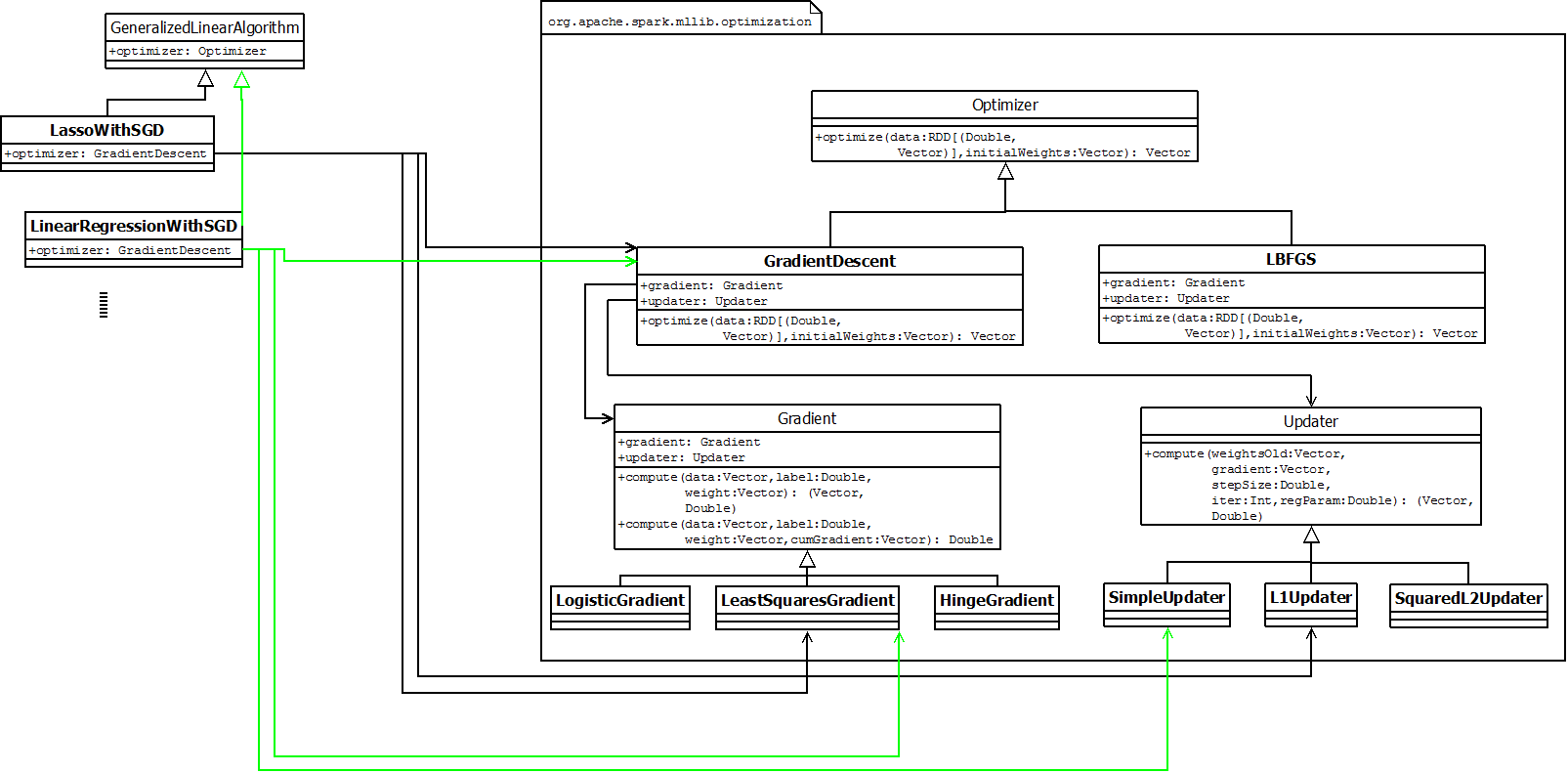
GLA，通用线性算法，作为通用回归算法（regression）和分类算法（classification）的抽象算法，run函数中实现了算法的流程，并最终产生通用线性模型。抽象算法流程主要包括：addIntercept, useFeatureScaling, 调用optimizer计算参数等。其中optimizer是抽象类，具体的线性算法需要指定具体的optimizer实现类。【模板模式——子类的训练大多调用了GLA中的run函数】

进一步地，optimizer是算法的核心，也是迭代算法的逻辑所在。具体类包括梯度下降等算法。这些优化算法又可以抽象并归纳出两个模块：梯度计算器（Gradient）和参数更新（Updater）。

综上，对于某一个具体的线性算法时主要一个优化器，而优化器是通过选择梯度计算器和参数更新器的组合来得到。【bridge pattern】

当前版本中GLA有多个子类，覆盖了多个分类和回归算法：

LassoWithSGD (org.apache.spark.mllib.regression)
LinearRegressionWithSGD (org.apache.spark.mllib.regression)
RidgeRegressionWithSGD (org.apache.spark.mllib.regression)
LogisticRegressionWithLBFGS (org.apache.spark.mllib.classification)
LogisticRegressionWithSGD (org.apache.spark.mllib.classification)
SVMWithSGD (org.apache.spark.mllib.classification)

例如，LinearRegressionWithSGD算法，对应的Optimizer是GradientDecent,对应的梯度计算器是LeaseSquareGradent，x位置的梯度$$\vec{\triangledown} = (\vec{x}^T\cdot\vec{w} - y)\cdot\vec{x}$$,对应的更新器为SimpleUpdater，更新算法是$$\vec{w} =: \vec{w} - \alpha / \sqrt{iter}\cdot\vec{\triangledown}/m$$

GeneralizedLinearModel

Algorithm will create a model by calling:

def createModel(...): M

**GeneralizedLinearModel **(GLM) represents a model trained using GeneralizedLinearAlgorithm. GLMs consist of a weight vector and an intercept.

Parameters:

weights - Weights computed for every feature.
intercept - Intercept computed for this model.

基本上每个线性算法都对应到一个线性模型：
LassoModel
LinearRegressionModel
LogisticRegressionModel
RidgeRegressionModel
SVMModel

GradientDecent梯度下降法

梯度下降法对convex函数必然能求解。

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)

%GRADIENTDESCENT Performs gradient descent to learn theta

% theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by

% taking num_iters gradient steps with learning rate alpha

% Initialize some useful values

m = length(y); % number of training examples

J_history = zeros(num_iters, 1);

for iter = 1:num_iters

% ====================== YOUR CODE HERE ======================

% Instructions: Perform a single gradient step on the parameter vector

% theta.

%

% Hint: While debugging, it can be useful to print out the values

% of the cost function (computeCost) and gradient here.

%

theta = theta - alpha * X' * (X * theta - y) / m;

% ============================================================

% Save the cost J in every iteration

J_history(iter) = computeCost(X, y, theta);

end

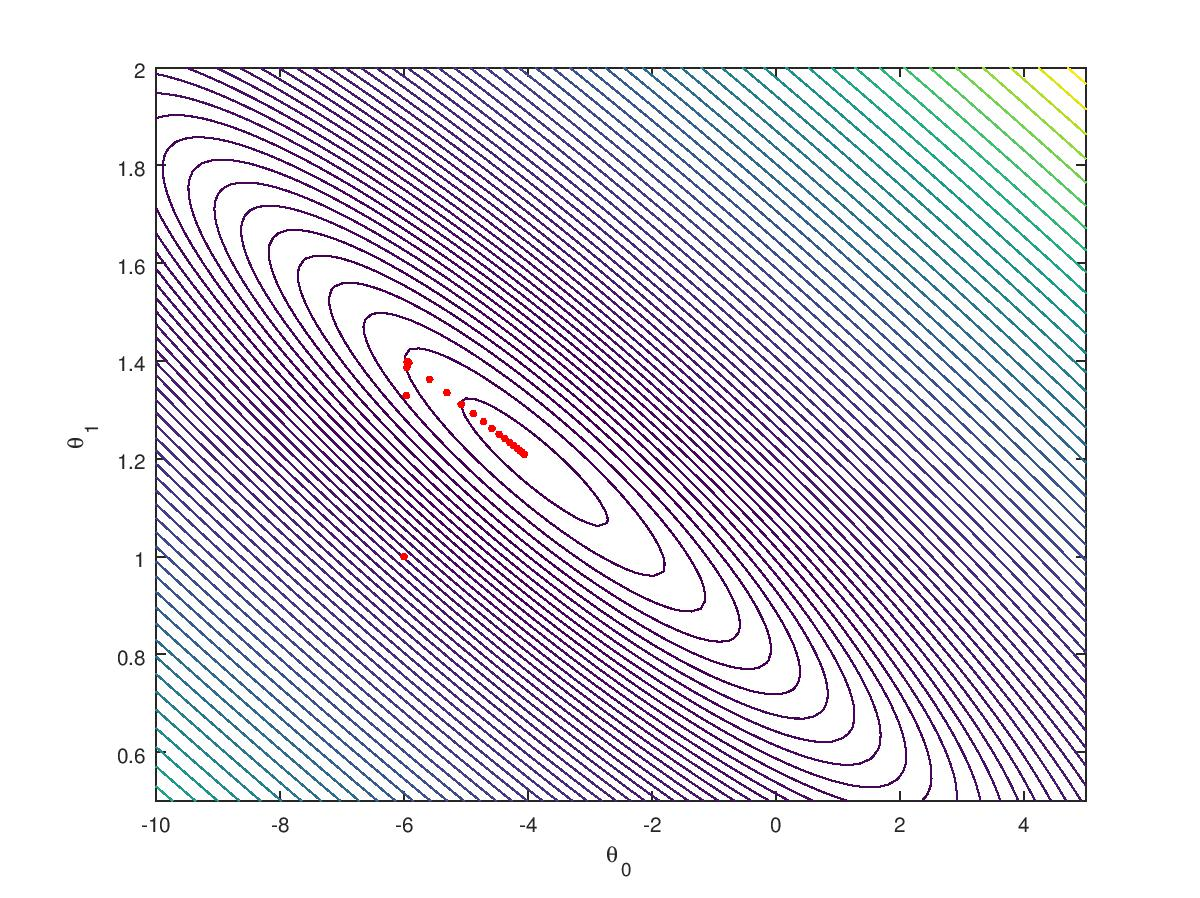
代码中可以发现多处使用了梯度下降法，包括ann，LR/SVM分类算法，Lasso/Linear/Ridge回归等算法。

主要构造函数：

class GradientDescent private[spark] (

private var gradient: Gradient,

private var updater: Updater)

extends Optimizer with Logging {

private var stepSize: Double = 1.0

private var numIterations: Int = 100

private var regParam: Double = 0.0

private var miniBatchFraction: Double = 1.0

private var convergenceTol: Double = 0.001

其中gradient为计算梯度的公式，updater为根据梯度的值去更新权重的公式。除了这两个参数之外，还有算法训练过程中的一些技术参数。

算法的基本参数设定之后便,再给定训练样本，便可以训练得到模型权重：

def optimize(

data: RDD[(Double, Vector)],

initialWeights: Vector): Vector = {

val (weights, _) = GradientDescent.runMiniBatchSGD(

data,

gradient,

updater,

stepSize,

numIterations,

regParam,

miniBatchFraction,

initialWeights,

convergenceTol)

weights

}

=> 调用迭代梯度下降法

def runMiniBatchSGD(data: RDD[(Double, Vector)],

gradient: Gradient,

updater: Updater,

stepSize: Double,

numIterations: Int,

regParam: Double,

miniBatchFraction: Double,

initialWeights: Vector,

convergenceTol: Double): (Vector, Array[Double])

Run stochastic gradient descent (SGD) in parallel using mini batches. In each iteration, we sample a subset (fraction miniBatchFraction) of the total data in order to compute a gradient estimate. Sampling, and averaging the subgradients over this subset is performed using one standard spark map-reduce in each iteration.

Parameters:

data - Input data for SGD. RDD of the set of data examples, each of the form (label, [feature values]).
gradient - Gradient object (used to compute the gradient of the loss function of one single data example)
updater - Updater function to actually perform a gradient step in a given direction.
stepSize - initial step size for the first step
numIterations - number of iterations that SGD should be run.
regParam - regularization parameter
miniBatchFraction - fraction of the input data set that should be used for one iteration of SGD. Default value 1.0.
initialWeights - initial weights for model training.
convergenceTol - Minibatch iteration will end before numIterations if the relative difference between the current weight and the previous weight is less than this value. In measuring convergence, L2 norm is calculated. Default value 0.001. Must be between 0.0 and 1.0 inclusively.

Returns:

A tuple containing two elements. The first element is a column matrix containing weights for every feature, and the second element is an array containing the stochastic loss computed for every iteration.

迭代梯度下降法 (SGD)

上述分析可以发现梯度下降法采用的实现法法是SGD，该算法对模型进行迭代更新，非常适合分布式计算，算法流程：

Sample a subset of data or just use all the data;
[MAPPER] for each entry, calculate gradient and model loss by Gradient $$(g^{(i)}, l^{(i)}) := \cal{Gradient}(x^{(i)}, y^{(i)}, \theta)$$;
[AGGREGATION] sum of gradient = $$\sum_ig^{(i)}$$, sum of loss = $$\sum_i l^{(i)}$$, counter = $$\sum_i 1$$;
Updater $$\theta' := \cal{Update}(\theta, \sum_ig^{(i)} / \sum_i 1, \alpha, ...)$$;
if $$||\theta'-\theta||_2 / ||\theta'||_2 < convergenceTol$$ finish, else $$\theta := \theta'$$, repeat from step 1.

各线性算法的G/U组合

Algorithm	optimizer	Gradient	updater
LinearRegressionWithSGD	GradientDescent	LeastSquares	Simple
LassoWithSGD	GradientDescent	LeastSquares	L1Updater
RidgeRegressionWithSGD	GradientDescent	LeastSquares	SquaredL2
LogisticRegressionWithSGD	GradientDescent	Logistic	SquaredL2
LogisticRegressionWithLBFGS	LBFGS	Logistic	SquaredL2
SVMWithSGD	GradientDescent	Hinge	SquaredL2

GradientDecent以及SGD算法的流程在上面已经描述，接下来具体分析各种梯度计算和权重更新算法：

`LeaseSquareGradent`

lost function:

\[L = 1/n ||X \cdot w - y||^2
\]

\[\vec x_i$$位置的梯度$$\vec{\triangledown_i} = (\vec{x_i}^T\cdot\vec{w} - \vec{y}_i)\cdot\vec{x_i}
\]

`SimpleUpdater`

A simple updater for gradient descent without any regularization.

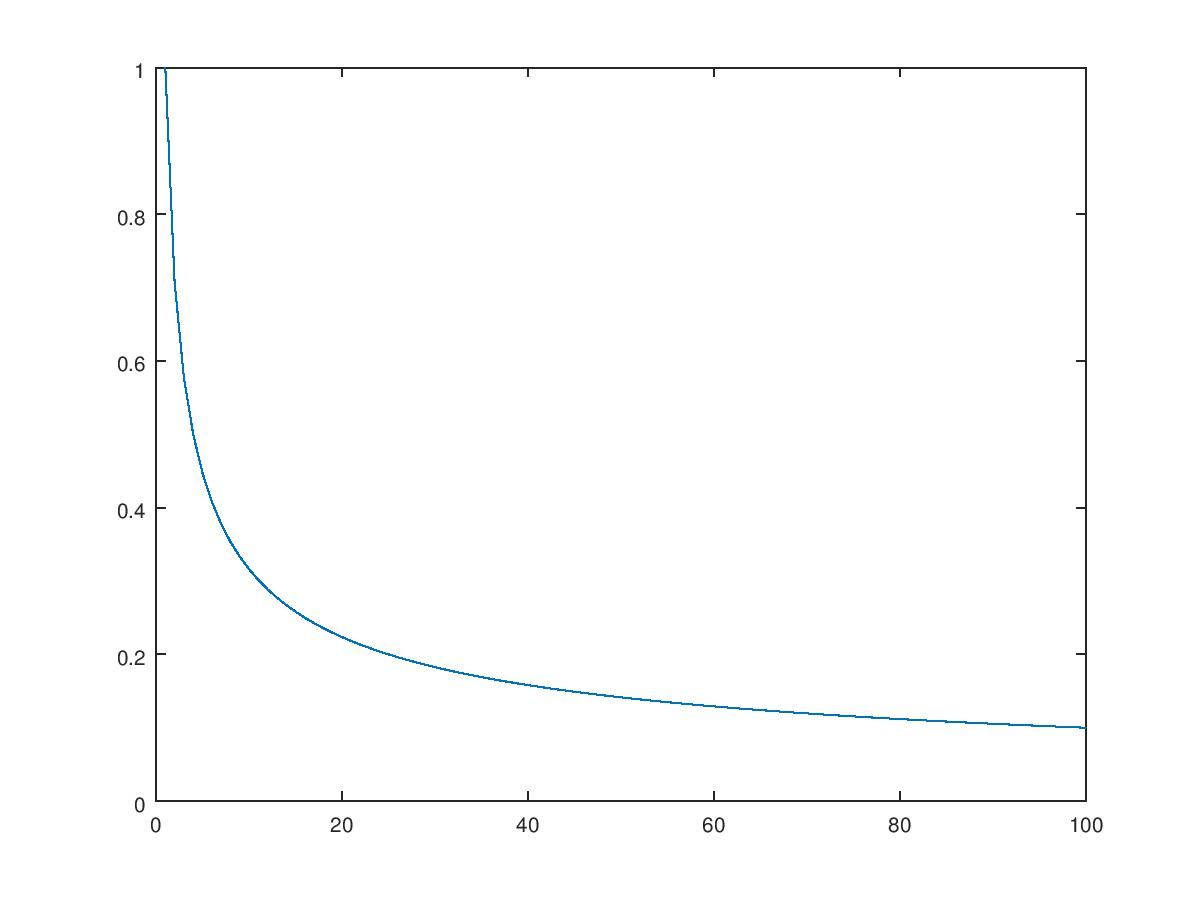
更新算法是$$\vec{w} := \vec{w} - \alpha / \sqrt{iter}\cdot\vec{\triangledown}$$，

其中$$ \vec{\triangledown} = \sum_i{\vec{\triangledown_i} / \sum_i {i}}$$

算法迭代过程中整体的步长会随着迭代次数而逐渐减小，

`SquaredL2Updater`

L2 regularized problems:

\[R(w) = \lambda /2 ||w||^2\\
L = 1/n ||X \cdot w - y||^2 + R(w),\\
\text{then:} \frac{dL}{dw}=\vec{\triangledown} + \lambda w\\
w:=w' - \alpha \cdot \frac{dL}{dw}\\
\ \ \ = (1-\alpha \lambda)\vec{w} - \alpha / \sqrt{iter}\cdot\vec{\triangledown}\]

与LinearRegressionWithSGD比较,RidgeRegressionWithSGD的优化器依然是LeastSquaresGradient，训练样本计算Gradient额算法也相同，不通点是在给定Gradient结果基础上更新权重时，old权重需要额外乘以一个系数。