python 回溯法 子集树模板 系列 —— 11、全排列

问题

实现 'a', 'b', 'c', 'd' 四个元素的全排列。

分析

这个问题可以直接套用排列树模板。

不过本文使用子集树模板。分析如下：

一个解x就是n个元素的一种排列，显然，解x的长度是固定的，n。

我们这样考虑：对于解x，先排第0个元素x[0]，再排第1个元素x[1]，...，当来到第k-1个元素x[k-1]时，就将剩下的未排的所有元素看作元素x[k-1]的状态空间，遍历之。

至此，套用子集树模板即可。

代码

'''用子集树实现全排列'''

n = 4
a = ['a','b','c','d']

x = [0]*n   # 一个解（n元0-1数组）
X = []      # 一组解

# 冲突检测：无
def conflict(k):
    global n, x, X, a

    return False # 无冲突

# 用子集树模板实现全排列
def perm(k): # 到达第k个元素
    global n, a, x, X

    if k >= n:  # 超出最尾的元素
        print(x)
        #X.append(x[:]) # 保存（一个解）
    else:
        for i in set(a)-set(x[:k]): # 遍历，剩下的未排的所有元素看作元素x[k-1]的状态空间
            x[k] = i
            if not conflict(k): # 剪枝
                perm(k+1)

# 测试
perm(0) # 从x[0]开始

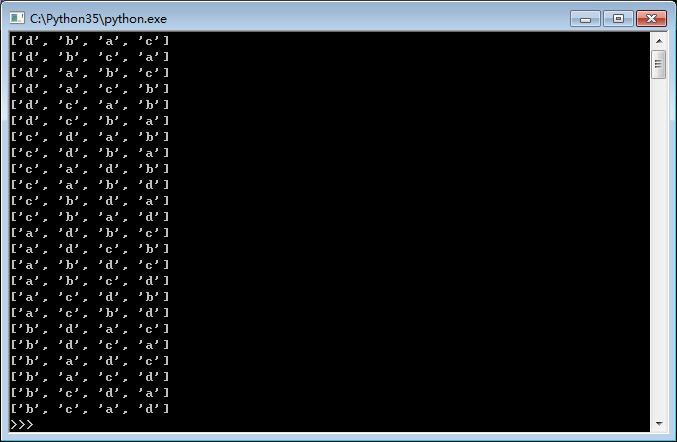
效果图