JavaScript图形实例:Koch曲线
Koch曲线的构造过程是:取一条长度为L0的直线段,将其三等分,保留两端的线段,将中间的一段改换成夹角为60度的两个等长直线;再将长度为L0/3的4个直线段分别进行三等分,并将它们中间的一段均改换成夹角为60度的两段长为L0/9的直线段;重复以上操作直至无穷,可得以一条具有自相似结构的折线,如图1所示。
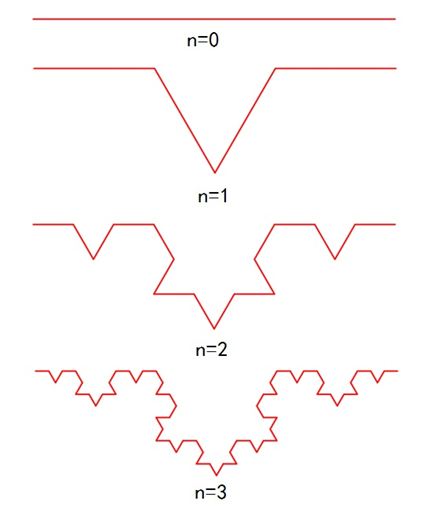
图1 Koch曲线的生成
Koch曲线采用递归过程易于实现,编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>Koch曲线</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="400" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var maxdepth =5;
var curdepth = 0;
ctx.lineWidth = 2;
Koch({x:50,y:150},{x:550,y:150},Math.PI/3);
function Koch(p1,p2,angle)
{
curdepth++;
if (curdepth<=maxdepth)
{
var x1=(2*p1.x+p2.x)/3;
var y1=(2*p1.y+p2.y)/3;
var x3=(2*p2.x+p1.x)/3;
var y3=(2*p2.y+p1.y)/3;
var x2=(x3-x1)*Math.cos(angle)-(y3-y1)*Math.sin(angle)+x1;
var y2=(x3-x1)*Math.sin(angle)+(y3-y1)*Math.cos(angle)+y1;
Koch(p1,{x:x1,y:y1},Math.PI/3);
Koch({x:x1,y:y1},{x:x2,y:y2},Math.PI/3);
Koch({x:x2,y:y2},{x:x3,y:y3},Math.PI/3);
Koch({x:x3,y:y3},p2,Math.PI/3);
}
if (curdepth>maxdepth)
draw([p1,{x:x1,y:y1},{x:x2,y:y2},{x:x3,y:y3},p2]);
curdepth--;
}
function draw(points)
{
ctx.strokeStyle = "red";
ctx.beginPath()
ctx.moveTo(points[0].x,points[0].y)
for(i=1;i<points.length;i++)
{
ctx.lineTo(points[i].x,points[i].y);
}
ctx.closePath()
ctx.stroke()
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出的Koch曲线,如图2所示。

图2 递归深度maxdepth =5的Koch曲线
由图1和2可知,Koch曲线的初始图元是直线,但最终结果却是一条参差不齐的曲线,很像雪花的边缘,如果将3条这样的曲线围在一起,便得到Koch雪花的图案。这样,初始图元不是一条直线,而是一个等边三角形。Koch雪花的生成示例如图3所示。

图3 Koch雪花的生成
在程序设计时,定义好等边三角形的三个顶点坐标,调用三次Koch递归过程,以实现等边三角形三条边各自的Koch曲线生成,即可得到Koch雪花图案。编写的HTML文件如下。
<!DOCTYPE html>
<head>
<title>Koch雪花</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var maxdepth =5;
var curdepth = 0;
ctx.lineWidth = 2;
Koch({x:50,y:450},{x:500,y:450},Math.PI/3);
Koch({x:275,y:450-225*Math.sqrt(3)},{x:50,y:450},Math.PI/3);
Koch({x:500,y:450},{x:275,y:450-225*Math.sqrt(3)},Math.PI/3);
function Koch(p1,p2,angle)
{
curdepth++;
if (curdepth<=maxdepth)
{
var x1=(2*p1.x+p2.x)/3;
var y1=(2*p1.y+p2.y)/3;
var x3=(2*p2.x+p1.x)/3;
var y3=(2*p2.y+p1.y)/3;
var x2=(x3-x1)*Math.cos(angle)-(y3-y1)*Math.sin(angle)+x1;
var y2=(x3-x1)*Math.sin(angle)+(y3-y1)*Math.cos(angle)+y1;
Koch(p1,{x:x1,y:y1},Math.PI/3);
Koch({x:x1,y:y1},{x:x2,y:y2},Math.PI/3);
Koch({x:x2,y:y2},{x:x3,y:y3},Math.PI/3);
Koch({x:x3,y:y3},p2,Math.PI/3);
}
if (curdepth>maxdepth)
draw([p1,{x:x1,y:y1},{x:x2,y:y2},{x:x3,y:y3},p2]);
curdepth--;
}
function draw(points)
{
ctx.strokeStyle = "red";
ctx.beginPath()
ctx.moveTo(points[0].x,points[0].y)
for(i=1;i<points.length;i++)
{
ctx.lineTo(points[i].x,points[i].y);
}
ctx.closePath()
ctx.stroke()
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,在浏览器窗口中可能会绘制出如图4所示的Koch雪花图案。

图4 递归深度maxdepth =5的Koch雪花图案
JavaScript图形实例:Koch曲线的更多相关文章
- JavaScript图形实例:线段构图
在“JavaScript图形实例:四瓣花型图案”和“JavaScript图形实例:蝴蝶结图案”中,我们绘制图形时,主要采用的方法是先根据给定的曲线参数方程计算出两点坐标,然后将两点用线段连接起来,线段 ...
- JavaScript动画实例:曲线的绘制
在“JavaScript图形实例:曲线方程”一文中,我们给出了15个曲线方程绘制图形的实例.这些曲线都是根据其曲线方程,在[0,2π]区间取一系列角度值,根据给定角度值计算对应的各点坐标,然后在计算出 ...
- JavaScript图形实例:再谈IFS生成图形
在“JavaScript图形实例:迭代函数系统生成图形”一文中,我们介绍了采用迭代函数系统(Iterated Function System,IFS)创建分形图案的一些实例.在该文中,仿射变换函数W的 ...
- JavaScript图形实例:随机SierPinski三角形
在“JavaScript图形实例:SierPinski三角形”中,我们介绍了SierPinski三角形的基本绘制方法,在“JavaScript图形实例:迭代函数系统生成图形”一文中,介绍了采用IFS方 ...
- JavaScript图形实例:Hilbert曲线
德国数学家David Hilbert在1891年构造了一种曲线,首先把一个正方形等分成四个小正方形,依次从西北角的正方形中心出发往南到西南正方形中心,再往东到东南角的正方形中心,再往北到东北角正方形中 ...
- JavaScript图形实例:四瓣花型图案
设有坐标计算公式如下: X=L*(1+SIN(4α))*COS(α) Y=L*(1+SIN(4α))*SIN(α) 用循环依次取α值为0~2π,计算出X和Y,在canvas画布中对坐标位置(X,Y)描 ...
- JavaScript图形实例:图形的旋转变换
旋转变换:图形上的各点绕一固定点沿圆周路径作转动称为旋转变换.可用旋转角表示旋转量的大小. 旋转变换通常约定以逆时针方向为正方向.最简单的旋转变换是以坐标原点(0,0)为旋转中心,这时,平面上一点P( ...
- JavaScript图形实例:圆内螺线
数学中有各式各样富含诗意的曲线,螺旋线就是其中比较特别的一类.螺旋线这个名词来源于希腊文,它的原意是“旋卷”或“缠卷”.例如,平面螺旋线便是以一个固定点开始向外逐圈旋绕而形成的曲线. 阿基米德螺线和黄 ...
- JavaScript图形实例:正多边形
圆心位于坐标原点,半径为R的圆的参数方程为 X=R*COS(θ) Y=R*SIN(θ) 在圆上取N个等分点,将这N个点首尾连接N条边,可以得到一个正N边形. 1.正多边形阵列 构造一个8行8列的正N( ...
随机推荐
- Java实现第十届蓝桥杯不同子串
试题 C: 不同子串 本题总分:10 分 [问题描述] 一个字符串的非空子串是指字符串中长度至少为 1 的连续的一段字符组成 的串.例如,字符串aaab 有非空子串a, b, aa, ab, aaa, ...
- Linux脚本安装包
脚本安装包 并不是独立的软件安装包类型,常见安装的是源码包,是人为把安装过程写成了自动安装的脚本,只要执行脚本,定义简答的参数,就可以实现安装,非常类似于Windows下软件的安装方式. 安装过程(安 ...
- 彻底搞懂 etcd 系列文章(二):etcd 的多种安装姿势
0 专辑概述 etcd 是云原生架构中重要的基础组件,由 CNCF 孵化托管.etcd 在微服务和 Kubernates 集群中不仅可以作为服务注册与发现,还可以作为 key-value 存储的中间件 ...
- ODEINT 求解常微分方程(3)
import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt # function tha ...
- Linux: ssh命令 远程登录
1.查看SSH客户端版本 使用ssh -V命令可以得到版本号.需要注意的是,Linux一般自带的是OpenSSH; $ ssh -V ssh: SSH Secure Shell 3.2.9.1 (no ...
- Linux中tomcat的部署
红帽7如何配置tomcat 1.下载tomcat9.0和java-1.8 tomcat的下载地址: https://tomcat.apache.org/ java1.8是radhat7自带: [roo ...
- bug的描述
我们知道了自身的症状,那么就从这里开始,一起聊一聊一个优秀的 BUG,应该包含哪些方面的内容呢? 标题 其实每一个 BUG 也都是一个小的文档,既然是文档,我们首先就要做好一个 “标题党”,当然,此 ...
- 1、安装配置Git私有服务器
安装并配置一个私有的Git服务器吧,这样自己的代码就可以进行版本控制了,当然版本控制的重要性嘛,Please Baidu. 系统环境:64位Win10 Version 1909 安装步骤: 1.下载j ...
- Python 偏函数用法全方位解析
Python的functools模块中有一种函数叫“偏函数”,自从接触它以来,发现确实是一个很有用且简单的函数,相信你看完这篇文章,你也有相见恨晚的感觉. 我们都知道,函数入参可以设置默认值来简化函数 ...
- Build completed with 1 error and 0 warnings in 20 ms
今天运行Idea,好端端的项目居然报了这个莫名其妙的错误Build completed with 1 error and 0 warnings in 20 ms. 首先排查下代码是否有问题,然后我就建 ...
