CF1327D Infinite Path 题解

CSDN同步

原题链接

太坑了我谔谔

简要题意：

求一个排列的多少次幂能达到另一个排列。排列的幂定义见题。（其实不是新定义的，本来就是这么乘的）

很显然，这不像快速幂那样可以结合律。

既然这样，就从图入手。

将 \(i\) 和 \(a_i\) 连边。

此时图会形成若干个环，对每个环分别操作。下面讲一个环的操作。

显然，对于一个环：

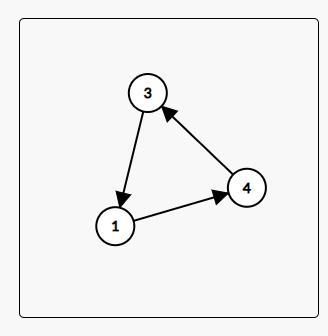
对于 \(1\) 这个点，\(k\) 次幂就是在环上走 \(k\) 步。

由于一个点的入度和出度都是 \(1\)，所以不会有重叠的环，因此是单向的。

所以，这题成了：在环上走很多步？

显然取 \(\gcd\) 即可。

但我们不知道步数，所以要枚举因数。

时间复杂度：\(O(T \times n)\).

实际得分：\(100pts\).

#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;

const int N=2e5+1;

inline int read(){char ch=getchar();int f=1;while(ch<'0' || ch>'9') {if(ch=='-') f=-f; ch=getchar();}
	int x=0;while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;}

int T,n,m,a[N],b[N];
int ans,tot,v[N];
bool h[N];

inline bool check(int x,int y) {
	for(int i=1,t;i<=x;i++) {
		t=i; bool f=0;
		for(int j=1;j<=y;j++) {
			if(b[v[t]]!=b[v[i]]) {
				f=1; break;
			} t=(t+x-1)%tot+1;
		} if(!f) return 1;
	} return 0;
} //对环检验

inline void dfs(int x) {
	tot=0; v[++tot]=x; h[x]=1;
	for(int i=a[x];i!=x;i=a[i]) h[i]=1,v[++tot]=i; //构成环
	for(int i=1;i<=sqrt(tot);i++)
		if(tot%i==0) {
			if(check(i,tot/i)) {
				ans=min(ans,i); return;
			} if(check(tot/i,i)) ans=min(ans,tot/i);
		} //枚举因数
}

int main(){
	T=read(); while(T--) {
		n=read(); memset(v,0,sizeof(v));
		memset(h,0,sizeof(h)); tot=0;
		for(int i=1;i<=n;i++) a[i]=read();
		for(int i=1;i<=n;i++) b[i]=read();
		ans=INT_MAX;
		for(int i=1;i<=n;i++)
			if(!h[i]) dfs(i);
		printf("%d\n",ans);
	}
	return 0;
}