数的划分（DFS、DP）

https://www.luogu.com.cn/problem/P1025

题目描述

将整数n分成k份，且每份不能为空，任意两个方案不相同(不考虑顺序)。

例如：n=7，k=3，下面三种分法被认为是相同的。

1,1,5;
1,5,1;
5,1,1.

问有多少种不同的分法。

输入格式

n,k (6<n≤200，2≤k≤6)

输出格式

1个整数，即不同的分法。

输入输出样例

输入 

输出

说明/提示

四种分法为：
1,1,5;
1,2,4;
1,3,3;
2,2,3.

解法一（DFS）：

DFS算是比较容易想到的，但需要剪枝。

void DFS(int sum,int step,int k)

k 表示上一份分了多少个，这次就从k个开始分，sum表示到目前为止一共分了多少个，step表示到目前为止一共分了多少份。

由于方案数不能相同，所以枚举的个数要保持递增(或递减)，我们可以进行重复性剪枝，记录k（上一份分了多少个），这次就从k个开始分起。

同时我们还要进行可行性剪枝，每次只要i从k枚举到i*(m - step) <= n-sum 就可以了。

因为下一份分的值不能比当前的i小，假设以后每份都分i，那么如果i*(m - step) > n-sum，则说明剩余的值不够分了，当前的i就不可行了，不需要继续DFS了。

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <string>
 #include <math.h>
 #include <algorithm>
 #include <vector>
 #include <stack>
 #include <queue>
 #include <set>
 #include <map>
 #include <sstream>
 const int INF=0x3f3f3f3f;
 typedef long long LL;
 const int mod=1e9+;
 const int maxn=1e4+;
 using namespace std;

 int n,m;
 int ans;

 void DFS(int sum,int step,int k)//k表示上一份分到了多少个,重复性剪枝
 {
     if(step==m)
     {
         if(sum==n) ans++;
         return ;
     }
     for(int i=k;i*(m-step)<=n-sum;i++)//可行性剪枝
         DFS(sum+i,step+,i);
 }

 int main()
 {
     #ifdef DEBUG
     freopen("sample.txt","r",stdin);
     #endif

     scanf("%d %d",&n,&m);
     DFS(,,);
     printf("%d\n",ans);

     return ;
 }

解法二（DP）：

dp[ i ][ j ]表示将整数 i 划分为 j 份 的方案数。

首先，如果拿到一个整数 i ，因为题目中要求每份不能为空，因此必须先拿出 j 个数位将 j 份分别放上1，此时剩下 i - j个数。

那么剩下的数如何处理呢？可以将其全部分到一份当中（dp[ i-j ][1]），也可以分到两份中(dp[ i-j ][2])，...，也可以分到 j 份中(dp[ i-j ][ j ])，将每一种分法全部加起来，和即为dp[ i ][ j ]。

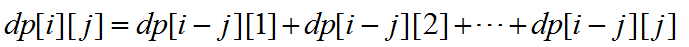
不过这个式子看起来并不简洁，为了求得一个简洁的式子，我们再求一个dp[i-1][j-1]，

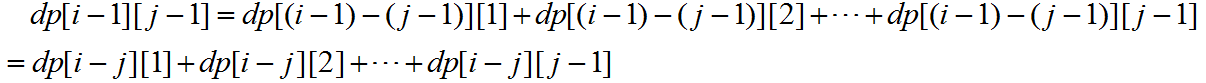
比较上面两个式子可得，

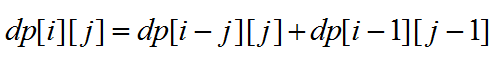
上式对应两种情况：

1.有一份只分了一个1，剩下的 i-1 要分成 j-1 份，对应dp[ i-1 ][ j-1 ]。
2.每一份的值都大于1，也就是先在j份中，每一份都放一个1，然后还剩下 i-j 个，再把这 i-j 个再分给这 j 份,对应dp[ i-j ][ j ]。（此时 i 必须大于 j )

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <string>
 #include <math.h>
 #include <algorithm>
 #include <vector>
 #include <stack>
 #include <queue>
 #include <set>
 #include <map>
 #include <sstream>
 const int INF=0x3f3f3f3f;
 typedef long long LL;
 const int mod=1e9+;
 const int maxn=1e4+;
 using namespace std;

 int dp[][];

 int main()
 {
     #ifdef DEBUG
     freopen("sample.txt","r",stdin);
     #endif

     int n,m;
     scanf("%d %d",&n,&m);
     for(int i=;i<=n;i++)
     {
         dp[i][]=;
         for(int j=;j<=m;j++)
         {
             if(i==j) dp[i][j]=;
             else if(i>j) dp[i][j]=dp[i-][j-]+dp[i-j][j];
         }
     }
     printf("%d\n",dp[n][m]);

     return ;
 }

-