DFS(深度优先搜索遍历求合格条件总数)--07--DFS--蓝桥杯方格填数

此题方法多种，我用规范的DFS来求解

题目：方格填数

如下的10个格子，填入0~9的数字。要求：连续的两个数字不能相邻。 
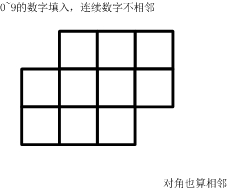
（左右、上下、对角都算相邻）一共有多少种可能的填数方案？ 
 

输出

请填写表示方案数目的整数。 

 #include <iostream>
 #include <vector>
 #include <stdio.h>
 #include <queue>
 #include <cmath>
 using namespace std;
 const int ROW = ;
 const int COL = ;

 int my[] = {};
 int sum = ;
 int num = ;

 int dd8[][] = {{-,},{,},{,},{,-},{-,},{,},{-,-},{,-}};
 int dd[][] = {{-,},{,},{,},{,-}};
 vector<vector<int> >sig[];
 vector<vector<int> >matrix(ROW,vector<int>(COL,-));

 bool check(int i,int j,int number){
     if(my[number] == )
         return false;
     for(int zz = ;zz < ;zz++){
         int ii = i + dd8[zz][];
         int jj = j + dd8[zz][];
         if(ii < ||jj < ||ii >= ROW||jj >= COL)
             continue;
         if(ii == &&jj ==)
             continue;
         if(ii == ROW - &&jj == COL - )
             continue;
         if(abs(matrix[ii][jj] - number) == )
             return false;
     }
     return true;
 }
 void rightload(){
     sig[sum] = matrix;
 }
 int checkrightload(){
     for(int k = ;k < sum;k++){
         if(sig[k] == matrix)
             return ;
     }
     return ;
 }
 void lock(int i,int j,int k){
     num--;
     my[k] = ;
     matrix[i][j] = k;
 }
 void unlock(int i,int j,int k){
     num++;
     my[k] = ;
     matrix[i][j] = -;
 }
 void dfs(int i,int j){
     for(int zz = ;zz < ;zz++){
         int ii = i + dd[zz][];
         int jj = j + dd[zz][];
         if(ii < ||jj < ||ii >= ROW||jj >= COL)
             continue;
         if(ii == &&jj ==)
             continue;
         if(ii == ROW - &&jj == COL - )
             continue;
         if(matrix[ii][jj] == -){
             for(int k = ;k < ;k++){
                 if(check(ii,jj,k) == true){
                     lock(ii,jj,k);
                     if(num == ){
                         if(checkrightload() == ){
                             rightload();
                             sum++;
                         }
                         unlock(ii,jj,k);
                         return;
                     }
                     else
                         dfs(ii,jj);
                     unlock(ii,jj,k);

                 }
             }
         }
     }
 }
 int main(){
     for(int i = ;i < ;i++){
         lock(,,i);
         dfs(,);
         unlock(,,i);
     }
     cout << sum <<endl;
     return ;
 }