算法总结篇---字典树（Trie）

写在前面
具体实现
- 引例：
- 引例代码：
例题

写在前面

字典树是一种清新通俗的数据结构（还是算法？）

顾名思义，字典树就是一棵像字典一样的树，可以用来查询某个单词是否出现过，查询过程就像查字典一样每个字符挨个找，看看是否有这个单词

具体实现

引例：

给你两个整数 $n$ 和 $m$ ，表示有 $n$ 个单词和 $m$ 次询问

在询问过程中，如果某个单词第一次被查到输出OK，如果不是第一次被查到输出REPEAT，如果没有该单词输出WRONG

先看一个样例

5

i

he

his

she

hers

3

hi

sheself

love

贴一个字典树成品图：

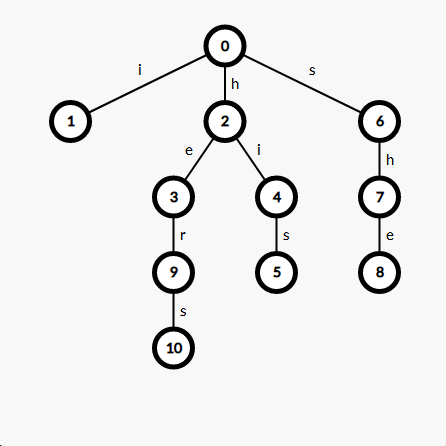
可以发现，生成的这棵字典树可以从根节点 $0$ 开始，找到所有给出的单词。举个栗子，$0 \to 2 \to 4 \to 5$ 表示的就是单词 his

字典树的结构还是比较简单的，我们用 $tr_{u,c}$ 表示结点 $u$ 通过 $c$ 字符指向的下一个结点，或者说在结点 $u$ 所代表的字符串中加一个字符 $c$ 后所在的新节点（$c$ 的取值与字符集有关，可根据题目具体要求来定）

相信大家已经发现 he 在 hers 的路径上有重叠，那么如何区分呢？

为了标记插入字典树的字符串，只需要每次插入完成时标记其所在的结点即可

放一个结构体封装的模板

struct Trie{

	int tr[MAXN][26], node_cnt = 0;//字典树以及结点个数

	bool cnt[MAXN];//标记是否是某个字符串的结尾

	void insert(char *s){//插入操作

		int now = 0, len = strlen(s + 1);//now表示当前所在的结点，len表示字符串长度

		for(int i = 1; i <= len; ++i){

			int ch = s[i] - 'a';//取出要插入的字符

			if(! tr[now][ch]) tr[now][ch] = ++node_cnt;

			//如果这个字符未被插入，新建一个结点将其插入

			now = tr[now][ch];//now指针跳向tr[now][ch]指向的位置

		}

		cnt[now] = true;//在字符串完成时所在的结点处打上标记

	}

	int find(char *s){//查询操作

		int now = 0, len = strlen(s + 1);//意义同上

		for(int i = 1; i <= len; ++i){

			int ch = s[i] - 'a';

			if(!tr[now][ch]) return false;//如果没有遍历到的字符，直接返回false

			now = tr[now][ch];//now指针跳向tr[now][ch]指向的位置

		}

		return cnt[now];

		//注意这里不能直接返回true，有可能查询的只是某个串的前缀，比如在样例中查询her

	}

} trie;

具体解释在注释里讲的很清楚了

引例代码：

只需要在查询返回时做一下标记处理即可

/*

Work by: Suzt_ilymics

Knowledge: ??

Time: O(??)

*/

#include<iostream>

#include<cstdio>

#include<cstring>

#include<algorithm>

#define LL long long

#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;

const int MAXN = 1e6+4;

const int INF = 1;

const int mod = 1;

int n, m;

char s[100];

int read(){

	int s = 0, f = 0;

	char ch = getchar();

	while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();

	while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();

	return f ? -s : s;

}

struct Trie{

	int tr[MAXN][26], node_cnt = 0;

	int cnt[MAXN];

	void insert(char *s){

		int now = 0, len = strlen(s + 1);

		for(int i = 1; i <= len; ++i){

			int ch = s[i] - 'a';

			if(! tr[now][ch]) tr[now][ch] = ++node_cnt;

			now = tr[now][ch];

		}

		cnt[now] = 1;

	}

	int find(char *s){

		int now = 0, len = strlen(s + 1);

		for(int i = 1; i <= len; ++i){

			int ch = s[i] - 'a';

			if(!tr[now][ch]) return 0;

			now = tr[now][ch];

		}

		if(cnt[now] == 1){

			cnt[now] = 2;

			return 1;

		}

		return 2;

	}

} trie;

int main()

{

	n = read();

	for(int i = 1; i <= n; ++i) cin >> s + 1, trie.insert(s);

	m = read();

	for(int i = 1; i <= m; ++i){

		cin >> s + 1;

		int ans = trie.find(s);

		if(ans == 0) printf("WRONG\n");

		else if(ans == 1) printf("OK\n");

		else printf("REPEAT\n");

	}

	return 0;

}

例题

Phone List

T组数据，每组数据给出n个长度不超过10数字串，问是否有一个串是另一个串的前缀

Solution：

朴素做法是 $n^{2}$ 判断，

考虑如何用字典树做，把n个数字串插入字典树，在从头遍历一遍看看是否是其他字符串的前缀，复杂度 $O(\sum\mid S \mid)$

稍微优化一下，在插入时判断。发现一个数是另一个数的前缀有两种可能，一是遍历过程中经过了其他标记过的结点，二是遍历结束后没有新建结点

Code

The XOR Largest Pair

在给定的 $N$ 个整数 $A_1,A_2,···A_n$ 中选出两个进行异或运算，得到的结果最大是多少？ $(0 \le n \le 2^{31} ) $

Solution

使用类似贪心的方法，先把 $n$ 个数插进去时，将其拆成二进制，先插高位再插低位

在 $O(n)$ 扫一遍所有数查询最大值，如果对应位数 $x \ xor \ 1$ 存在，就走 $tr[now][x \ xor \ 1]$ ，否则走 $tr[now][x]$，遍历过程中统计答案即可，最后对所有答案取最大值

Code

L语言

给定由 $n$ 个单词组成的字典，有 $m$ 段文章，输出一段文章从前向后理解最多能理解多少。

规定一段字符串被理解当且仅当这一段字符串是字典中的某整个单词

Solution:

建树不多说了，

在理解一段文章时，因为每当一段字符是字典中的整个单词，都可以被理解，那么从前向后遍历，对于某个位置，如果它是某个单词的结尾，那么它的下一个位置可以重新从根节点中开始匹配。在匹配过程中如果发现遍历到的结点是某个单词的结尾，将其标记，方便下一次匹配。匹配过程中顺便记录最后一个被标记的单词的结尾的位置。

Code