hdu 6814 Tetrahedron 规律+排列组合逆元

题意：

给你一个n，你需要从1到n（闭区间）中选出来三个数a,b,c（可以a=b=c），用它们构成一个直角四面体的三条棱（可看图），问你从D点到下面的三角形做一条垂线h，问你1/h²的期望

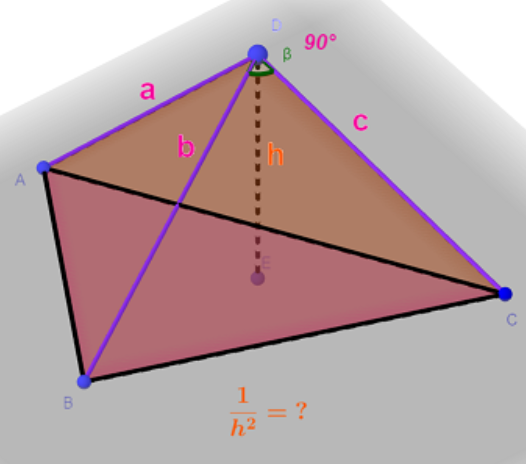
题解：

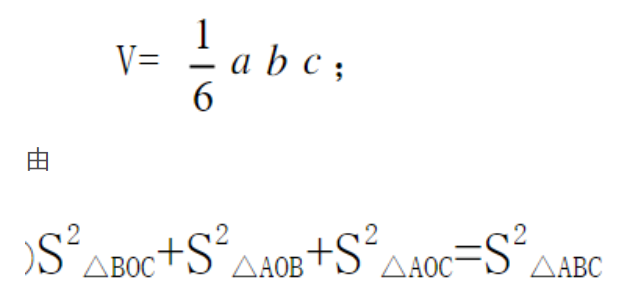
那么1/h²=1/a²+1/b²+1/c²

总数就是n³

之后就是找分子怎么求，规律：

 (（1/a1*a1)*n*n+(1/a2*a2)*n*n+(1/a_n*a_n)*n*n)/(n*n*n)

a的取值从1到n

代码：

#include<stack>
#include<queue>
#include<map>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define fi first
#define se second
using namespace std;
typedef long long ll;
const int maxn=6e6+1;
const int mod=998244353;
ll dp[maxn];
ll ksc(ll a, ll b)
{
    ll ans = 0;
    while( b > 0 )
    {
        if( b&1 ) ans = (ans + a) % mod;
        a = ( a + a ) % mod;
        b >>= 1;
    }
    return ans;
}
ll ppow(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1) ans=(ans*a)%mod;
        a=(a*a)%mod;
        b>>=1;
    }
    return ans;
}
int main()
{
    //printf("%d\n",(15*ppow(8,mod-2))%mod);
    ll ans = 0;
    for (ll i = 1; i <= 6000001; i++)
    {
        ll x = ((i * i) % mod);
        ans = (ans + (ppow(x, mod - 2) % mod));
        dp[i] = (ans * 3) % mod;
    }
    ll t;
    scanf("%lld",&t);
    while(t--)
    {
        ll n;
        scanf("%lld",&n);
        printf("%lld\n",(ksc(dp[n],ppow(n,mod-2)))%mod);
    }
    return 0;
}