用x种方式求第n项斐波那契数，99%的人只会第一种

大家好啊，我们又见面了。听说有人想学数据结构与算法却不知道从何下手？那你就认真看完本篇文章，或许能从中找到方法与技巧。

    本期我们就从斐波那契数列的几种解法入手，感受算法的强大与奥妙吧。

原文链接：原文来自个人公众号：C you again，欢迎关注

斐波那契数列

    斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”。

    斐波那契数列指的是这样一个数列：

0、1、1、2、3、5、8、13、21、34......

    有一组数列，它的第一项为1，第二项为1，从第三项开始，每一项为前两项之和。

    斐波那契数列的第n项Fn可以通过如下的递归公式定义：

F(1)=1，F(2)=1,

F(n)=F(n-1)+F(n-2)（n ≥ 3，n ∈ N*）

通项公式

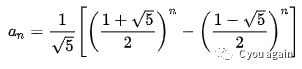
    如上，又称为“比内公式”，是用无理数表示有理数的一个范例。

注：此时a1=1，a2=1，a(n)=a(n-1)+a(n-2)，（n ≥ 3，n ∈ N*）

求第n项斐波那契数

    现在写一个函数int fib(int n) 返回第n项Fn。例如，若n=0，则函数fib(0)应该返回0，若n=1, 则函数fib(1)应返回1，若 n > 1，返回 F(n-1)+F(n-2)。

若n = 9

输出：34

    下面是返回斐波那契数列第n项Fn的不同方法：

方法1 (使用递归)

    一个简捷的方法是直接使用递归定义关系式写出递归实现的代码，C/C++代码如下：

//Fibonacci Series using Recursion
#include<stdio.h>
int fib(int n) {
    if (n <= 1)
        return n;
    return fib(n - 1) + fib(n - 2);
}

int main() {
    int n = 9;
    printf("%d", fib(n));

    return 0;
}

输出：34

时间复杂度：T(n) = T(n-1) + T(n-2)，该时间复杂度是指数级别的

空间复杂度：如果考虑递归调用时栈的大小，则为O(n) ；如果不考虑调用栈的话，则为O(1)

    通过观察，我们可以发现递归求解时做了很多重复的工作(见下面的递归调用树)。因此采用递归方式求解斐波那契数列的第n项Fn不是一种好的方法。



方法2 (使用动态规划Dynamic Programming：DP)

    如果你还不了解动态规划，请看以下两篇文章：

    《深入浅出理解动态规划（一） | 交叠子问题》

    《深入浅出理解动态规划（二） | 最优子结构》

    在方法1中，在求解某项时，如果我们把计算结果存储起来，则后续的计算就可以使用前面的计算结果，从而可以避免很多重复的计算，C/C++代码如下：

//Fibonacci Series using Dynamic Programming
#include<stdio.h>

int fib(int n) {
    /* Declare an array to store Fibonacci numbers. */
    int f[n + 1];
    int i;

    /* 0th and 1st number of the series are 0 and 1*/
    f[0] = 0;
    f[1] = 1;

    for (i = 2; i <= n; i++) {
        /* Add the previous 2 numbers in the series
         and store it */
        f[i] = f[i - 1] + f[i - 2];
    }

    return f[n];
}

int main() {
    int n = 9;
    printf("%d", fib(n));

    return 0;
}

输出：34

时间复杂度：O(n)

空间复杂度: O(n)

方法3 (对方法2进行空间上的优化)

    由于在计算某项时只需其前面相邻的两项，因此可以对方法2中的空间进行优化，C/C++代码如下：

// Fibonacci Series using Space Optimized Method
#include<stdio.h>
int fib(int n) {
    int a = 0, b = 1, c, i;
    if (n == 0)
        return a;
    for (i = 2; i <= n; i++) {
        c = a + b;
        a = b;
        b = c;
    }
    return b;
}

int main() {
    int n = 9;
    printf("%d", fib(n));

    return 0;
}

输出：34

时间复杂度: O(n)

空间复杂度: O(1)

    当然，也可以使用滚动数组。滚动数组不是什么高大上的技术，我们在计算斐波那契数列的过程中，始终使用相邻的前两项，加上正在计算的项，总共就三项，因此可以定义一个长度只有3的数组，可以滚动地使用0、1、2这三个下标。代码如下：

//Fibonacci Series using Dynamic Programming
#include<stdio.h>

int fib(int n) {
    /* Declare an array to store Fibonacci numbers. */
    int f[3];       /* 只需定义一个长度为3的数组 */
    int i;

    /* 0th and 1st number of the series are 0 and 1*/
    f[0] = 0;
    f[1] = 1;

    for (i = 2; i <= n; i++) {
        /* Add the previous 2 numbers in the series
         and store it：注意下标要对3取模 */
        f[i % 3] = f[(i - 1) % 3] + f[(i - 2) % 3];
    }

    return f[n % 3]; /* 这里要注意下标对3取模 */
}

int main() {
    int n = 9;
    printf("%d", fib(n));

    return 0;
}

方法4 (使用矩阵{{1,1},{1,0}}的幂)

    另外一种复杂度为O(n)的方法是对矩阵M={{1,1},{1,0}}自乘n次(换句话说，就是计算矩阵M的n次幂：power(M,n)), 这样就可以在结果矩阵下标为(0, 0)的地方得到斐波那契数列的第(n+1)项，如下所示：

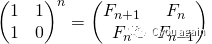
#include <stdio.h>

/* Helper function that multiplies 2 matrices F and M of size 2*2, and puts the multiplication result back to F[][] */
void multiply(int F[2][2], int M[2][2]);

/* Helper function that calculates F[][] raise to the power n and puts the result in F[][]。Note that this function is designed only for fib() and won't work as general power function */
void power(int F[2][2], int n);

int fib(int n) {
    int F[2][2] = { { 1, 1 }, { 1, 0 } };
    if (n == 0)
        return 0;
    power(F, n - 1);

    return F[0][0];
}

void multiply(int F[2][2], int M[2][2]) {
    int x = F[0][0] * M[0][0] + F[0][1] * M[1][0];
    int y = F[0][0] * M[0][1] + F[0][1] * M[1][1];
    int z = F[1][0] * M[0][0] + F[1][1] * M[1][0];
    int w = F[1][0] * M[0][1] + F[1][1] * M[1][1];

    F[0][0] = x;
    F[0][1] = y;
    F[1][0] = z;
    F[1][1] = w;
}

void power(int F[2][2], int n) {
    int i;
    int M[2][2] = { { 1, 1 }, { 1, 0 } };

    // n - 1 times multiply the matrix to {{1,0},{0,1}}
    for (i = 2; i <= n; i++)
        multiply(F, M);
}

/* Driver program to test above function */
int main() {
    int n = 9;
    printf("%d", fib(n));

    return 0;
}

输出：34

时间复杂度: O(n)

空间复杂度: O(1)

方法 5 (对方法4进行优化 )

    上面的方法4可以优化到)的时间复杂度。我们可以像计算x^n那样，采用递归的方式来计算power(M, n) ，C/C++代码如下：

#include <stdio.h>

void multiply(int F[2][2], int M[2][2]);

void power(int F[2][2], int n);

/* function that returns nth Fibonacci number */
int fib(int n) {
    int F[2][2] = { { 1, 1 }, { 1, 0 } };
    if (n == 0)
        return 0;
    power(F, n - 1);
    return F[0][0];
}

/* Optimized version of power() in method 4 */
void power(int F[2][2], int n) {
    if (n == 0 || n == 1)
        return;
    int M[2][2] = { { 1, 1 }, { 1, 0 } };

    power(F, n / 2);
    multiply(F, F);

    if (n % 2 != 0)
        multiply(F, M);
}

void multiply(int F[2][2], int M[2][2]) {
    int x = F[0][0] * M[0][0] + F[0][1] * M[1][0];
    int y = F[0][0] * M[0][1] + F[0][1] * M[1][1];
    int z = F[1][0] * M[0][0] + F[1][1] * M[1][0];
    int w = F[1][0] * M[0][1] + F[1][1] * M[1][1];

    F[0][0] = x;
    F[0][1] = y;
    F[1][0] = z;
    F[1][1] = w;
}

/* Driver program to test above function */
int main() {
    int n = 9;
    printf("%d", fib(n));

    return 0;
}

输出：34

时间复杂度: O(Logn)

空间复杂度: 如果考虑递归调用时栈的大小，则为O(n) ；如果不考虑调用栈的话，则为O(1)

方法 6 (O(Log n) 的时间复杂度)

    下面是一个很有趣的计算斐波那契数列第n项的递归公式，该公式的时间复杂度为O(Log n)。

如果n是偶数， 则k=n/2，

F(n)=[2F(k-1)+F(k)]F(k)

如果n是奇数，则 k=(n+1)/2

F(n)=F(k)F(k)+F(k-1)F(k-1)

原文链接：原文来自个人公众号：C you again，欢迎关注

    该公式是如何计算的？上面的公式可以从前面的矩阵幂推算出来：





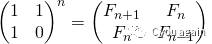
要证明上面的公式成立，只需做下面的工作即可：

如果n是偶数, 令 k = n/2

如果n是奇数, 令 k = (n+1)/2

    下面是上述过程的C++ 实现：

// C++ Program to find n'th fibonacci Number in
// with O(Log n) arithmatic operations
#include <bits/stdc++.h>
using namespace std;

const int MAX = 1000;

// Create an array for memoization
int f[MAX] = { 0 };

// Returns n'th fuibonacci number using table f[]
int fib(int n) {
    // Base cases
    if (n == 0)
        return 0;
    if (n == 1 || n == 2)
        return (f[n] = 1);

    // If fib(n) is already computed
    if (f[n])
        return f[n];

    int k = (n & 1) ? (n + 1) / 2 : n / 2;

    // Applyting above formula [Note value n&1 is 1
    // if n is odd, else 0.
    f[n] = (n & 1) ?
            (fib(k) * fib(k) + fib(k - 1) * fib(k - 1)) :
            (2 * fib(k - 1) + fib(k)) * fib(k);

    return f[n];
}

/* Driver program to test above function */
int main() {
    int n = 9;
    printf("%d ", fib(n));
    return 0;
}

输出：34

时间复杂度为：O(Log n) ，因为每次递归调用时都将问题规模降了一半

方法 7 (使用Java提供的BigInteger类)

     Java提供了BigInteger类，可以很轻易地算出当n很大时的斐波那契数。

// Java program to compute n-th Fibonacci number where n may be large.
import java.math.*;

public class Fibonacci {
    // Returns n-th Fibonacci number
    static BigInteger fib(int n) {
        BigInteger a = BigInteger.valueOf(0);
        BigInteger b = BigInteger.valueOf(1);
        BigInteger c = BigInteger.valueOf(1);
        for (int j = 2; j <= n; j++) {
            c = a.add(b);
            a = b;
            b = c;
        }

        return (a);
    }

    public static void main(String[] args) {
        int n = 1000;
        System.out.println("Fibonacci of " + n + "th term" + " " + "is" + " " + fib(n));
    }
}

当n=1000时，输入结果如下：

原文链接：原文来自个人公众号：C you again，欢迎关注

公众号推荐（资源加油站）

了解更多资源请关注个人公众号：C you again,你将收获以下资源

1、PPT模板免费下载，简历模板免费下载

2、基于web的机票预订系统，基于web的图书管理系统

3、贪吃蛇小游戏源码

4、各类IT技术分享

文章推荐

推荐一：计算机网络中这些高频考题，你还在死记硬背吗？（一），讲述内容：IP地址及其分类，子网掩码的概念，网络号、主机号、直接广播地址计算方法等。

推荐二：计算机网络中这些高频考题，你还在死记硬背吗？（二），讲述内容：局域网接口配置、路由器的静态路由配置、OSPF动态路由协议配置和DHCP服务器配置。

    以上就是本期的所有内容了，是否对你有帮助呢？了解更多算法请关注公众号“C you again”。