背包问题(动态规划 C/C++)

Description

卖方：这件商品14元买方：给你20元卖方：不好意思，我的零钱不够买方：好吧，这是15元，剩的当小费

当到一个地方旅游时，如果你买东西的地方不支持信用，带零钱还是非常有用的。特别是有时候卖方没有零钱，如果你没有刚好的钱，你需要支付比卖价多一点。

当然你想付尽量少的钱（至少是商品价值的钱）。并且，当支付最少钱的时候，也最好是支付的硬币的数量最少。

Input

第一行包含一个整数表示测试数据的组数。每组测试数据每一行包含一个整数，表示你需要付的钱数，钱数不超过10000元。接下来包含一个整数n，表示你所拥有的钱的数量，n最多是100,接下来的n行每行一个整数，表示你有的每个硬币的面值，注意钱的面值可以是任意的，不和我们现在用的面值一样，钱的面值不超过10000元。

Output

对每组测试数据，在一行上输出两个整数：需要支付的钱数和数量。

Sample Input

Sample Output

1500 2

动态规划问题，当成0-1背包处理，也可以当成多重背包。

这里当成0-1背包处理即可，物品最多就100种，每种取或不取

dp[j]是价值j需要dp[j]张钱

dp[j]先初始化正无穷，表示价值j的没有钱可以凑出j

dp[0] = 0，表示0元需要0张钱。

递推公式：

$$ dp[j]\ = \ \begin{cases} min(dp[j\ -\ num[i]]\ +\ 1,\ dp[j]) &\ i = 1 -> n,\ j = 20000 -> num[i] \end{cases} $$

也可以用二维数组，只不过开辟的空间大

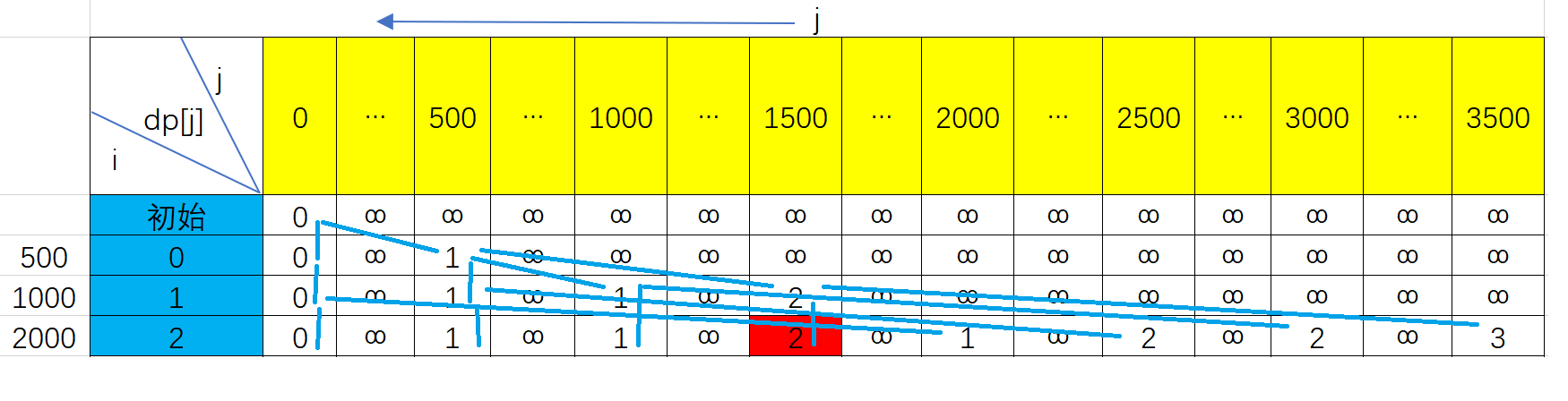
dp[i][j]表示前i张面值可以组成价值j的最少张数

dp[i][j]全部初始化正无穷，dp[0][0] = 0

递推公式：

$$ dp[i][j]\ = \ \begin{cases} min(dp[i\ -\ 1][j\ -\ num[i]]\ +\ 1,\ dp[i\ -\ 1][j]) &\ j >= num[i] \\ dp[i\ -\ 1][j] &\ 0 <= j < num[i] \\ \end{cases} $$

最后找dp[j]，从j = 输入的价钱，开始找满足条件且价钱最小的

AC代码：

#include <iostream>

#include <algorithm>

#include <cstring>

using namespace std;

int dp[20001];

int main()

{

	ios::sync_with_stdio(false);		// 避免cout, cin导致TLE

	int n;

	cin >> n;			// n组测试数据

	while (n--)

	{

		memset(dp, 0x7f, sizeof(dp));		// dp全部置正无穷

		dp[0] = 0;							// 第一个元素置零

		int price, money_nums;				// price是价钱, money_nums是钱的张数

		cin >> price >> money_nums;

		int money[100];						// 钱面值数组

		for (int i = 0; i < money_nums; i++)

			cin >> money[i];

		for (int i = 0; i < money_nums; i++)

			for (int j = 20000; j >= money[i]; j--)			// 逆序进行

				dp[j] = min(dp[j], dp[j - money[i]] + 1);	// 递推公式

		for (int i = price; i <= 20000; i++)

		{

			if (dp[i] <= 100)		// 找到第一个满足钱数最小的, 并且张数小于100, dp[i]已经是最优的

			{

				cout << i << ' ' << dp[i] << endl;			// 输出结果

				break;

			}

		}

	}

	return 0;

}

一开始数组开10000，提交通过了

后来发现，有些测试数据应该通过不了

比如：

19998 2

之前的代码会什么都不输出，

把数组开成20000就行了。

之前没考虑这种特殊情况，碰巧通过了