Pytorch Autograd (自动求导机制)

Pytorch Autograd (自动求导机制)

---

Introduce

Pytorch Autograd库 (自动求导机制) 是训练神经网络时，反向误差传播(BP)算法的核心。

本文通过logistic回归模型来介绍Pytorch的自动求导机制。首先，本文介绍了tensor与求导相关的属性。其次，通过logistic回归模型来帮助理解BP算法中的前向传播以及反向传播中的导数计算。

以下均为初学者笔记。

---

Tensor Attributes Related to Derivation

note: 以下用x代表创建的tensor张量。

• x.requires_grad：True or False，用来指明该张量在反向传播过程中是否需要求导。
• with torch.no_grad():：当我们在做模型评估的时候是不需要求导的，可以嵌套一层with torch.no_grad()以减少可能的计算和内存开销。
• x.grad：返回损失函数对该张量求偏导的值，在调用backward()之后才有。
• x.grad_fn：存储计算图上某中间节点进行的操作，如加减乘除等，用于指导反向传播时loss对该节点的求偏导计算。
• x.is_leaf：True or False，用于判断某个张量在计算图中是否是叶子张量。叶子张量我个人认为可以理解为目标函数中非中间因变量（中间函数），如神经网络中的权值参数w就是叶子张量。
• x.detach()：返回tensor的数据以及requires_grad属性，且返回的tensor与原始tensor共享存储空间，即一个改变会导致另外一个改变。因此，如果我们在backward之前对x.detach()返回的张量进行改变会导致原始x的改变，从而导致求导错误，但是这时系统会报错提醒。
  
  （note：虽然x.data也与x.detach()作用相似，但是x.data不被Autograd系统追踪，因此如果遇到上述问题并不会报错。推荐使用x.detach()）
• x.item()：如果张量只包含一个元素，可以用x.item()返回，通常loss只包含一个数值，因此常用loss.item()。
• x.tolist()：如果张量只包含多个元素，可以用x.tolist()转换成python list返回。

---

Build Logistic regression Model

假设有一个损失函数如下（Logistic回归）：

\[z = w1x1+w2x2+b
\]

\[y_p = sigmoid(z)
\]

\[Loss(y_p,y_t) = -{1\over n}\sum_{i=1}^n (y_tlog(y_p)+(1-y_t)log(1-y_p))
\]

摘自吴恩达机器学习

由损失函数构建简单计算图模型如下：

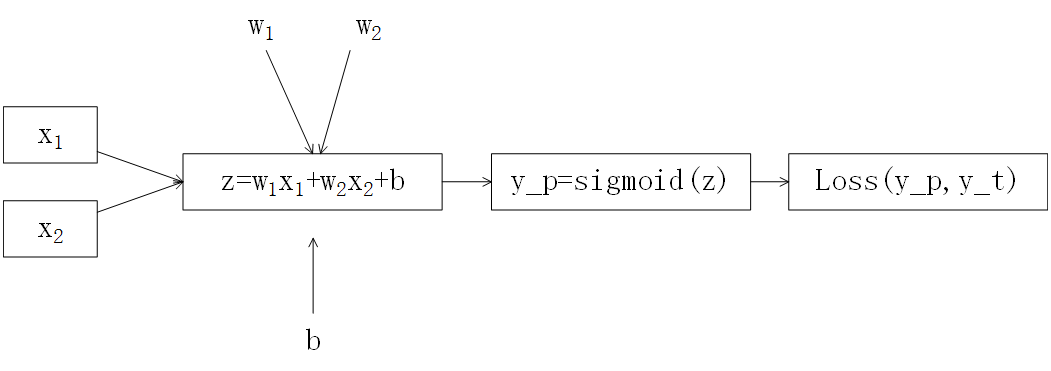
现在我们通过上述例子来理解前向传播和反向传播。在上述简单的神经网络模型中，我们需要对权值参数w1，w2以及阈值参数b进行更新。神经网络训练的总体过程如下：先由输入层逐级前向传播计算loss输出，再有输出层loss反向计算各层梯度传播误差，以此更新各层的权值参数w和阈值参数b。

在该模型中我们需要求出loss对w1、w2以及b的偏导，以此利用SGD更新各参数。对于根据链式法则的逐级求导过程不再赘述，吴恩达机器学习SGD部分有详细的计算过程以及解释。

现在我们利用pytorch实现logistic回归模型，并手动实现参数更新。

import torch
import numpy as np

# 读入数据 x_t,y_t
x_t = torch.tensor(np.array([[1,1],[1,0],[0,1],[0,0]]),requires_grad=False,dtype=torch.float)
y_t = torch.tensor([[0],[1],[0],[1]],requires_grad=False,dtype=torch.float)
print(x_t.size())
# 定义权值参数w和阈值参数b
w = torch.randn([2,1], requires_grad=True,dtype=torch.float)
b = torch.zeros(1, requires_grad=True,dtype=torch.float)
print(w.size())
# 构建逻辑回归模型
def logistic_model(x_t):
    a = torch.matmul(x_t,w) + b
    return torch.sigmoid(a)

y_p = logistic_model(x_t)

# 计算误差
def get_loss(y_p, y_t):
    return -torch.mean(y_t * torch.log(y_p)+(1-y_t) * torch.log(1-y_p))

loss = get_loss(y_p, y_t)
print(loss)

# 自动求导
loss.backward()

# 查看 w 和 b 的梯度
print(w.grad)
print(b.grad)

# 更新一次参数
w.data = w.data - 1e-2 * w.grad.data
b.data = b.data - 1e-2 * b.grad.data

'''
note:
存在两个问题：
1. 如果没有前面先更新一次参数，后面直接进行迭代更新的话，会报错，具体原因也没搞懂。
2. 利用pycharm运行pytorch代码，调用了backward()之后，程序运行完成进程并不会终止，需要手动到任务管理器中kill进程，具体原因也不清楚。
'''

# epoch
for e in range(10000):  # 进行 10000 次更新
    y_p = logistic_model(x_t)
    loss = get_loss(y_p, y_t)

    w.grad.zero_()  # 记得归零梯度
    b.grad.zero_()  # 记得归零梯度
    loss.backward()

    w.data = w.data - 1e-2 * w.grad.data  # 更新 w
    b.data = b.data - 1e-2 * b.grad.data  # 更新 b
    print('epoch: {}, loss: {}'.format(e, loss.data.item()))

print(w)
print(b)

'''
每500次迭代打印出输出结果，我们看到损失函数在迭代中逐步下降：
epoch: 0, loss: 0.9426676034927368
epoch: 500, loss: 0.5936437249183655
epoch: 1000, loss: 0.4318988025188446
epoch: 1500, loss: 0.33194077014923096
epoch: 2000, loss: 0.265964150428772
epoch: 2500, loss: 0.22003984451293945
epoch: 3000, loss: 0.18663322925567627
epoch: 3500, loss: 0.1614413857460022
epoch: 4000, loss: 0.14187511801719666
epoch: 4500, loss: 0.12630191445350647
epoch: 5000, loss: 0.11365044862031937
epoch: 5500, loss: 0.10319262742996216
epoch: 6000, loss: 0.09441888332366943
epoch: 6500, loss: 0.08696318417787552
epoch: 7000, loss: 0.08055643737316132
epoch: 7500, loss: 0.07499672472476959
epoch: 8000, loss: 0.07013023644685745
epoch: 8500, loss: 0.06583743542432785
epoch: 9000, loss: 0.06202460825443268
epoch: 9500, loss: 0.05861698091030121
至此，手动实现梯度下降，logistic模型搭建完成，之后将尝试利用pytorch框架搭建神经网络。

'''

---

本文参考-1

本文参考-2