晚间测试3 B. 单(single)

题目描述

单车联通大街小巷.这就是出题人没有写题目背景的原因.

对于一棵树,认为每条边长度为 $1$,每个点有一个权值$a[i]$.$dis(u,v)$为点$u$到$v$的最短路径的边数.$dis(u,u)=0$.对每个点求出一个重要程度.点$x$的重要程度$b[x]$定义为其他点到这个点的距离乘上对应的点权再求和. 即:$b[x]=a[1]*dis(1,x)+a[2]*dis(2,x)+....+a[n]*dis(n,x)$

现在有很多树和对应的$a$数组，并求出了$b$数组.不幸的是，记录变得模糊不清了.幸运的是,树的形态完好地保存了下来,$a$数组和$b$数组至少有一个是完好无损的,但另一个数组完全看不清了.

希望你求出受损的数组.多组数据.

输入格式

第一行输入一个$T$，表示数据组数。接下来$T$组数据。

每组数据的第$1$行$1$个整数$n$表示树的点数.节点从$1$到$n$编号.

接下来$n-1$行每行两个整数$u,v$表示$u$和$v$之间有一条边.

接下来一行一个整数$t$，表示接下来数组的类型。

$t=0$则下一行是$a$数组，$t=1$则下一行是$b$数组。

接下来一行$n$个整数，表示保存完好的那个数组，第$i$个数表示$a[i]$或$b[i]$。

输出格式

$T$行，每组数据输出一行表示对应的$a$数组或$b$数组，数组的相邻元素用一个空格隔开。忽略行末空格和行尾回车.

样例

样例输入

2

2

1 2

1

17 31

2

1 2

0

31 17

样例输出

31 17

17 31

数据范围与提示

对于$100\%$的数据，$T=5,2<=n<=100000,1<=u,v<=n$,保证给出的$n-1$条边形成一棵树

对于$100\%$的数据，$t=0$或$t=1,1<=a[i]<=100,1<=b[i]<=10^9$，$t=1$时保证给出的$b$数组对应唯一的一个$a$数组。

对于$100\%$的数据，单个输入文件不会包含超过$2000000$个整数，这段话可以理解为，你不必考虑输入输出对程序运行时间的影响。

对于$100\%$的数据，保证答案不会超过$int$能表示的范围

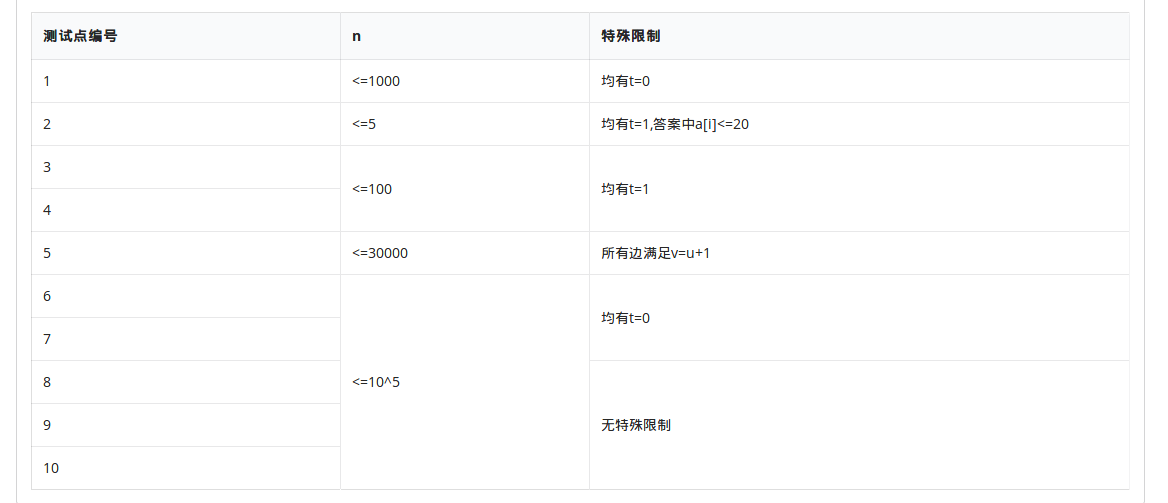
接下来的表格中描述了每个测试点的具体特征。每个测试点的$5$组数据均符合表格中对应的特征。

分析

默认 $1$ 号节点为根节点

我们设 $sum[i]$ 为以 $i$ 为根的子树中 $a$ 数组的和

当 $t=0$ 时，显然是一个换根 $DP$，有 $b[now]=b[fa]+sum[1]-sum[now]-sum[now]$

当 $t \neq 0$ 时，如果数据范围较小的话可以进行高斯消元

但是这道题的 $n$ 比较大，所以我们只能推式子

由换根 $DP$ 的式子，我们可以得到对于除$1$之外的任何节点都有 $b[now]-b[fa]=sum[1]-2sum[now]$

我们把这些式子相加，可以得到 $x_1b[1]+x_2b[2]+...+x_nb[n]=(n-1)sum[1]-2 \sum_{i=2}^nsum[now]$

对于左边这一堆，我们可以 $dfs$ 求出每一个节点对应的系数 $x_i$，从而得到左边的值

对于右边的 $\sum_{i=2}^nsum[now]$，其实就是 $b[1]$

因为我们在换根 $DP$ 的第一个 $dfs$ 时会有 $b[1]= \sum_{u=son\ of\ 1}sum[u]+g[u]$

其中 $g[u]=\sum_{v=son\ of\ u}sum[v]+g[v]$

当递归到叶子节点时，会有$g[u]=sum[u]=a[u]$

所以$\sum_{i=2}^nsum[now]=b[1]$

我们带入上面的式子就可以求出 $sum[1]$

进行一遍 $dfs$ 可以求出所有节点的$sum$值

再进行一遍 $dfs$ 就可以求出所有节点的$a$值

代码

#include<cstdio>

#include<cstring>

#include<cmath>

#include<algorithm>

#include<iostream>

#define int long long

inline int read(){

	int x=0,fh=1;

	char ch=getchar();

	while(ch<'0' || ch>'9'){

		if(ch=='-') fh=-1;

		ch=getchar();

	}

	while(ch>='0' && ch<='9'){

		x=(x<<1)+(x<<3)+(ch^48);

		ch=getchar();

	}

	return x*fh;

}

const int maxn=1e6+5;

int n,head[maxn],tot=1,t;

struct asd{

	int to,next;

}b[maxn];

void ad(int aa,int bb){

	b[tot].to=bb;

	b[tot].next=head[aa];

	head[aa]=tot++;

}

void clr(){

	memset(head,-1,sizeof(head));

	memset(&b,0,sizeof(b));

	tot=1;

}

int zd[maxn];

int f[maxn],g[maxn],siz[maxn],sum;

void dfs1(int now,int fa){

	siz[now]=zd[now];

	for(int i=head[now];i!=-1;i=b[i].next){

		int u=b[i].to;

		if(u==fa) continue;

		dfs1(u,now);

		g[now]+=g[u]+siz[u];

		siz[now]+=siz[u];

	}

}

void dfs2(int now,int fa){

	if(now==1){

		f[now]=g[now];

	}

	for(int i=head[now];i!=-1;i=b[i].next){

		int u=b[i].to;

		if(u==fa) continue;

		f[u]=f[now]+sum-siz[u]-siz[u];

		dfs2(u,now);

	}

}

void solve1(){

	memset(siz,0,sizeof(siz));

	memset(f,0,sizeof(f));

	memset(g,0,sizeof(g));

	sum=0;

	for(int i=1;i<=n;i++){

		sum+=zd[i];

	}

	dfs1(1,0);

	dfs2(1,0);

	for(int i=1;i<=n;i++){

		printf("%lld ",f[i]);

	}

	printf("\n");

}

int nans,ncnt,xs[maxn];

void dfs3(int now,int fa){

	for(int i=head[now];i!=-1;i=b[i].next){

		int u=b[i].to;

		if(u==fa) continue;

		dfs3(u,now);

		xs[u]++;

		xs[now]--;

	}

}

void dfs4(int now,int fa){

	for(int i=head[now];i!=-1;i=b[i].next){

		int u=b[i].to;

		if(u==fa) continue;

		siz[u]=(siz[1]+zd[now]-zd[u])/2;

		dfs4(u,now);

	}

}

void dfs5(int now,int fa){

	for(int i=head[now];i!=-1;i=b[i].next){

		int u=b[i].to;

		if(u==fa) continue;

		siz[now]-=siz[u];

		dfs5(u,now);

	}

}

void solve2(){

	memset(siz,0,sizeof(siz));

	memset(xs,0,sizeof(xs));

	dfs3(1,0);

	nans=0;

	for(int i=1;i<=n;i++){

		nans+=(1LL*zd[i]*xs[i]);

	}

	siz[1]=nans-ncnt*zd[1];

	siz[1]+=2*zd[1];

	siz[1]/=(n-1);

	dfs4(1,0);

	dfs5(1,0);

	for(int i=1;i<=n;i++){

		printf("%lld ",siz[i]);

	}

	printf("\n");

}

signed main(){

	freopen("single.in","r",stdin);

	freopen("single.out","w",stdout);

	t=read();

	while(t--){

		clr();

		n=read();

		int aa,bb,op;

		for(int i=1;i<n;i++){

			aa=read(),bb=read();

			ad(aa,bb);

			ad(bb,aa);

		}

		op=read();

		for(int i=1;i<=n;i++){

			zd[i]=read();

		}

		if(op==0){

			solve1();

		} else {

			solve2();

		}

	}

	return 0;

}