【学习笔记】最小直径生成树（MDST）

简介

无向图中某一点（可以在顶点上或边上），这个点到所有点的最短距离的最大值最小，那么这个点就是 图的绝对中心。

无向图所有生成树中，直径最小的一个，被称为 最小直径生成树。

图的绝对中心的求法

下文设 $d(i, j)$ 为顶点 $i,j$ 间的最短路径长。

首先我们考虑枚举每一条边 $(u, v)$，长为 $L$，并假设绝对中心 $p$ 在这条边上并且距离 $u$ 长为 $x(\le L)$。

对于图中一点 $i$，$p$ 到 $i$ 的距离可以写作 $d(p, i) = \min(d(u, i) + x,\ d(v, i) + (L - x))$。

那么显然可以看出 $d(p, i)$ 的函数图像是一个 两条斜率相同的线段构成的折线段。

于是 $p$ 到最远点距离的函数可以写作 $f = \max\limits_{1\le i\le n}\{d(p, i)\}$，图像是一堆折线组成的更加曲折的折线，如图（来源）：

图中的 $\alpha$ 即为文中的 $x$，$\omega_{u, v}$ 即为 $L$，$w_{1\cdots n}$ 为图中异于 $u, v$ 的点。

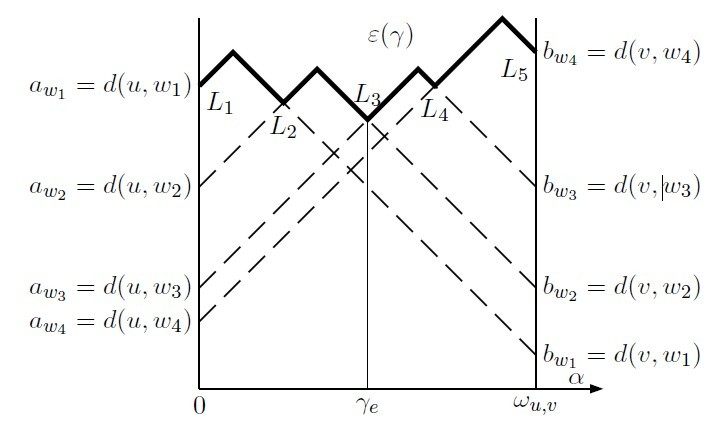
那么答案即为图像中的最低点，横坐标即为绝对中心的位置。

如何得到最低点？不难观察到最低点必然是两折线的交点。

对于图中的两点 $i, j$，若 $d(u, i) \ge d(u, j)$ 且 $d(v, i) \ge d(v, j)$，那么显然这个 $j$ 是丝毫不用考虑的——可以看出 $d(p, j)$ 的函数图像是完全位于 $d(p, i)$ 下方的，最低点显然不会在此。

这样筛出的 $t$ 条折线会有 $t - 1$ 个交点，那么只要根据这些交点更新答案即可。

$O(t^2)$ 暴力枚举？大可不必。可以观察到，有一个性质，若我们将这些折线 按 $d(u, i)$ 的大小 升序排序，那么对应 $d(v, i)$ 的大小是 递减的。

于是排序后相邻两折线必定会有交点。

图的绝对中心的实现

设 $adj(i, j)$ 为结点 $i, j$ 间的直接距离（边长），$d(i, j)$ 如上文所述，$rk(i, j)$ 为距离点 $i$ 第 $j$ 远的点，$f$ 即上文的函数。

这里 $ans$ 表示最远距离。

首先使用多源最短路算法（Floyd，Johnson 等）求出 $d$ 数组。
求出 $rk$，对于每一个 $i$，按关键字 $d(i, j)$ 降序排序。
然后对于每一个点或边对答案进行更新：
- 可能在点上：对于每一个点 $i$，用相对较远的点更新：$ans \leftarrow \min(ans, d(i, rk(i, 1)))$。
- 可能在边上：对于每一条边 $(i, j)$，从距离 $i$ 最远的点开始验证——对于所有的 $k(\le n)$：
  - 若 $d(j, rk(i, k-1)) \le d(j, rk(i, k))$，因为 $rk$ 是根据 $d(i, \cdots)$ 排序的，那么两者组合，发现这个对答案无贡献，不能计算，跳过。
  - 否则就是 $f$ 上的一个可能为答案的点（交点）。更新答案：$ans\leftarrow \min(ans, \dfrac{d(i, rk(i, k)) + d(i, rk(i, k - 1)) + adj(i, j)}{2})$。

最后 $ans$ 即为所求。如果需要具体位置需要特别地在更新 $ans$ 时记录。

复杂度 $O(n^3 + nm)$ 或 $O(nm\log n + nm)$，区别在于多源最短路的求法。对于无权图还可以直接 Bfs 得到更优秀的效率。

最小直径生成树（MDST）的求法

根据定义，易知图的绝对中心必定为 MDST 直径的中点。

那么只要得到绝对重心，MDST 并不难求——从绝对中心开始，生成一个最短路径树即为 MDST。

显然 MDST 的直径大小为 $ans\times 2$。

习题

BZOJ 2180 - 最小直径生成树 / SPOJ MDST - Minimum Diameter Spanning Tree 【参考代码】
SPOJ PT07C - The GbAaY Kingdom 【参考代码】
Codeforces 266D - BerDonalds

后记

原文地址：https://www.cnblogs.com/-Wallace-/p/13483433.html
本文作者：@-Wallace-
转载请附上出处。