敏捷史话（八）：敏捷的破局之道——Martin Fowler

在 Martin Fowler 的世界里，任何事情都有最优解。

1963年，Martin 出生于英格兰的沃尔索尔（Walsall），也在同样位于沃尔索尔的玛丽女王文法学校中接受中等教育。在这里的乡村中，他度过了一段简单、愉快的少年时光。

上了中学之后，Martin 接触到了策略桌游。在桌游的“厮杀”中， 如何从复杂的局势中找出最简洁、直观的破局之法，就成为他想要寻找的答案，也成为日后他解决任何事情的目标。

1986年，Martin 毕业于伦敦大学学院，获得了电子工程与计算机科学的学士学位。自此，Martin 踏入了软件领域。

重构

毕业后，Martin 分别在 Coopers & Lybrand 和一家名为 Ptech 的小型科技公司工作了一段时间。之后，又作为一名独立顾问，为世界各地的公司提供相应的帮助。

在观察了多家公司的工作模式之后，Martin 发现， 由于软件需要不断地修复 Bug 并添加新特性，这会让原本的代码库变得繁杂，导致之后的工作进度越来越缓慢。

举一个很简单的例子：假设我们有一个抽屉，最初，里面只有三四样物品，这样我们很轻松地就能找到并拿出某一物品。但当抽屉内放置的物品越来越多时，再想要找到特定的物品就非常困难了。

那么，如何用一种简单、直观的方式来解决这一问题呢？Martin 想到，为了应对更改逐渐叠加的这一情况，可以用重构代码来减少这些不必要的复杂性。于是，Martin 开始筹备《重构》一书，希望能够将代码重构的实践带给更多的公司与团队。

1991年《重构》出版发行，这本书成功地推动了“重构”实践的普及，帮助程序员们编写出易懂、易维护的代码，同样也开辟了一个“炒熟饭”的市场，指导了企业或开发者，如何将“烂代码”重构。这之后，Martin 又分别于2013年和2018年出版了《重构：Ruby 版本》及《重构：改进现有代码的设计》，以指导职业 Ruby 程序员实践重构，并指出：重构并不是出现在项目计划中的一项特殊任务，而应该是编程活动中的一个常规部分。

Martin 认为，重构其实很简单，只需将复杂的事情拆分开。

《敏捷宣言》

随着应用软件的蓬勃发展，软件开发的升级成本越来越高，Martin Fowler 开始转而追寻软件开发的最佳实践，“轻量”方法论渐入人们的视野。

随后，Martin 为了形成全面运动的核心，开始同 Robert C. Martin、Alistair Cockburn 着手组织一个关于“轻量”方法论的聚会。

会中，Martin 与 Ward Cunningham 两人对会议进行了全面的调节，快速制定出了会议流程与决策方法。就这样，雪鸟会议开始了。

回忆起二十年前的那场会议，Martin 认为，参与雪鸟会议的这十七个人并没有什么特殊之处，他们也并不是唯一拥有这些价值观和原则的人。他们在随后掀起的敏捷运动中没有任何特殊的地位，也并没有要把自己建立在这样一个地位上的愿望。

实际上， 对于敏捷软件的未来，每个人都拥有发言权。

“bliki”的诞生

对 Martin 来说，记录是一个非常好的习惯。一方面，在与行业伙伴进行深入交流后，能够产生一些灵感碰撞产生的火花；另一方面，他会亲自思考实践并抽象总结，然后通过出版物、博客、网站等，同大家分享自己的理念。

Martin 的写作之路，早在20世纪就出现了苗头。90年代末，Martin Fowler 为《分布式计算》写了一篇专栏。同时，Martin 接触到了一位出版社编辑，也陆续在 Addison-Wesley 公司出版了一系列的书籍，包括：《分析模式：可重用对象模型》、《UML 精粹：标准对象建模语言的简明指南》、《重构：改进现有代码的设计》等。

在21世纪初，Martin Fowler 又在《IEEE软件》杂志的设计专栏做了五年的编辑。这几段专栏作者以及编辑的经历让 Martin 体验了从文章产出、校对到发表的全流程。与需要经过复杂校对审核的流程相比，Martin 更倾向于自己掌握主导权。

与此同时，blog 开始流行，很多人开始迈入 blog 大军的行列，Martin 也跃跃欲试。但在接触了 blog 后不久，他对此有了一些微词。在他看来，blog 中简短的文字就如同天空中的烟花： 稍纵即逝、无法保留。给他类似感受的，还有 wiki——一个很容易就会导致信息复杂、冗长的网站。因此，他决定创建一个介于 wiki 和 blog 之间的网站，既能像 blog 一样发布一些简短的想法，又能像 wiki 一样建立一个交叉链接的主体。

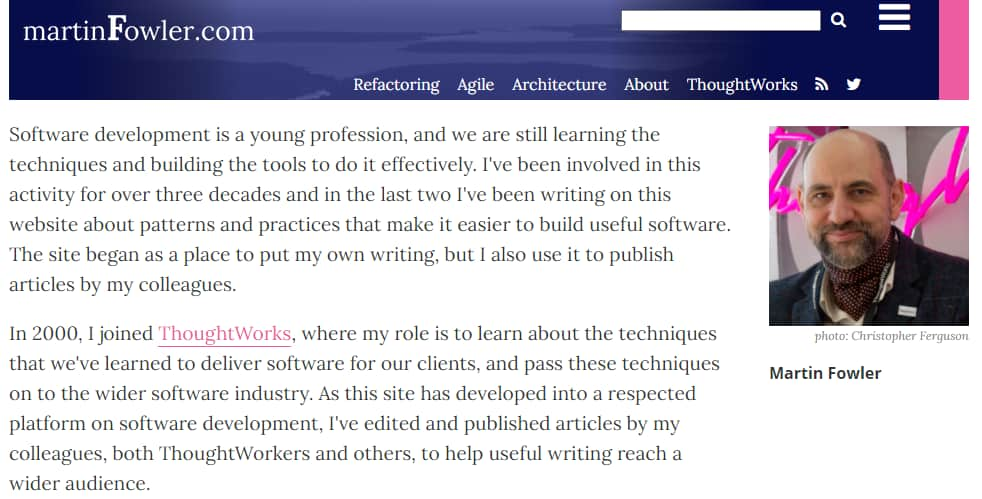
很快，一个名为“martinfowler.com”的 bliki 网站诞生了。一开始，Martin 会在网站上时不时地更新自己的文章，文章内容涵盖了软件开发领域的方方面面。随着网站越来越受欢迎，他认为，是时候以这一网站为平台来帮助更多作者增加曝光度了。所以，Martin 开始在网站中逐步增加他人的文章，并对收到的每一篇文章都进行仔细地审查，以确保网站内容的质量。

现今，已年近古稀的 Martin Fowler，同妻子住在波士顿市郊。在工作之余，他们会去度假、摄影、徒步，也会将沿路的风景、人文分享给自己的读者。这些日常不仅带给了 Martin 很多工作中的灵感，也激发了他写作的动力。或许， 问题的最优解，就藏在生活的每一处小细节中。