【Codeforces549F】Yura and Developers [单调栈][二分]

Yura and Developers

Time Limit: 20 Sec  Memory Limit: 512 MB

Description

　　

Input

　　

Output

　　

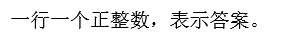
Sample Input

　　4 3
　　5 2 4 4

Sample Output

　　2

HINT

　　

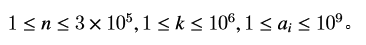
Solution

　　首先，我们先用单调栈求出以点 i 作为最大值的区间 [pre_i,  suc_i]。然后显然就是 求 [pre_i, suc_i] 内有几个区间的和与val[i] %k同余。

　　我们记区间为 [L, mid, R]（i 为mid，pre_i 为 L，suc_i 为R），显然我们可以枚举长度小的半个区间。这时效率是O(nlogn)的。

　　那么只要能求出另外一半的贡献即可，假定我们枚举 [L, mid - 1] 的一个 点begin。那么 [begin, mid - 1] 的和是固定的，我们又知道总和应该为多少（%k同余）。所以我们就可以知道剩下需要提供多少值。 问题就转化为了求：[mid, mid ~ R] 中有几个以 mid 为左端点，mid~R为右端点的区间 的和 %k余 一个定值。

　　我们考虑这个东西怎么求，显然可以将问题转化为查前缀和形式：

　　　　我们已知 [1, mid - 1] 的和%k的值，又由于[mid, mid~R] 要提供一个定值的贡献，所以可以算出 [1, mid~R] 要余多少。

　　那么我们就可以通过查前缀和解决这个子问题，现在的问题又转化为了 如何查询一个区间 [L, R] 内某一定值数的个数：

　　　　显然我们可以 把位置加入在一个以值为下标的vector中，在这个vector中，二分查询位置<=R的个数即可，减去 <=(L - 1) 的即可。

　　这样我们就解决了假定[L, mid - 1]固定的一部分，假定[mid + 1, R]固定同理。

　　我们就解决了这道题啦！QWQ

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 #include<vector>
 using namespace std;
 typedef long long s64;

 const int ONE = ;
 const int MOD = 1e9 + ;

 int n, k;
 s64 val[ONE];
 int pre[ONE], suc[ONE];
 s64 sum[ONE], sum_B[ONE];
 s64 Ans;

 vector <int> A[ONE], B[ONE];

 int get()
 {
         int res;char c;
         while( (c=getchar())< || c> );
         res=c-;
         while( (c=getchar())>= && c<= )
         res=res*+c-;
         return res;
 }

 void Deal_first()
 {
         int stk[ONE], top = ;
         for(int i = ; i <= n; i++)
         {
             while(top && val[i] > val[stk[top]])
                 suc[stk[top--]] = i - ;
             pre[i] = stk[top] + ;
             stk[++top] = i;
         }
         while(top) suc[stk[top--]] = n;

         for(int i = ; i <= n; i++)
             sum[i] = (sum[i - ] + val[i]) % k;
         for(int i = n; i >= ; i--)
             sum_B[i] = (sum_B[i + ] + val[i]) % k;

         for(int i = ; i <= n; i++)
         {
             A[sum[i]].push_back(i);
             B[sum_B[i]].push_back(i);
         }
 }

 int Get(int l, int r)
 {
         int res = sum[r] - sum[l - ];
         if(res < ) res += k;
         return res;
 }
 int Find(int R, int val)
 {
         if(A[val].size() == ) return ;
         int l = , r = A[val].size() - ;
         while(l < r - )
         {
             int mid = l + r >> ;
             if(A[val][mid] > R) r = mid;
             else l = mid;
         }
         if(A[val][l] > R) return l;
         if(A[val][r] > R) return r;
         return A[val].size();
 }
 int Query_left(int L, int R, int val) //sum [L,L~R] num of val
 {
         if(L > R) return ;
         int now = sum[L - ]; //[1, L - 1]
         int need = (now + val) % k; //1 ~ R the num of presum = need
         return Find(R, need) - Find(L - , need);
 }
 void Deal_left(int l, int mid, int r)
 {
         int T = val[mid] % k;
         for(int i = l; i <= mid - ; i++)
         {
             int now = Get(i, mid - );
             int need = (T - now + k) % k;
             Ans += Query_left(mid, r, need);
         }

         Ans += Query_left(mid, r, T) - ;
 }

 int Get_B(int l, int r)
 {
         int res = sum_B[l] - sum_B[r + ];
         if(res < ) res += k;
         return res;
 }
 int Find_B(int R, int val)
 {
         if(B[val].size() == ) return ;
         int l = , r = B[val].size() - ;
         while(l < r - )
         {
             int mid = l + r >> ;
             if(B[val][mid] > R) r = mid;
             else l = mid;
         }
         if(B[val][l] > R) return l;
         if(B[val][r] > R) return r;
         return B[val].size();
 }
 int Query_right(int L, int R, int val)
 {
         if(L > R) return ;
         int now = sum_B[R + ];
         int need = (now + val) % k;
         return Find_B(R, need) - Find_B(L - , need);
 }
 void Deal_right(int l, int mid, int r)
 {
         int T = val[mid] % k;
         for(int i = mid + ; i <= r; i++)
         {
             int now = Get_B(mid + , i);
             int need = (T - now + k) % k;
             Ans += Query_right(l, mid, need);
         }
         Ans += Query_right(l, mid, T) - ;
 }

 int main()
 {
         n = get();    k = get();
         for(int i = ; i <= n; i++)
             val[i] = get();

         Deal_first();

         for(int i = ; i <= n; i++)
         {
             if(i - pre[i] +  <= suc[i] - i + )
                 Deal_left(pre[i], i, suc[i]);
             else
                 Deal_right(pre[i], i, suc[i]);
         }

         printf("%lld", Ans);
 }