CTC (Connectionist Temporal Classification) 算法原理
(原创文章,转载请注明出处哦~)
简单介绍CTC算法
CTC是序列标注问题中的一种损失函数。
传统序列标注算法需要每一时刻输入与输出符号完全对齐。而CTC扩展了标签集合,添加空元素。
在使用扩展标签集合对序列进行标注后,所有可以通过映射函数转换为真实序列的 预测序列,都是正确的预测结果。也就是在无需数据对齐处理,即可得到预测序列。
其目标函数就是 最大化 所有正确的预测序列的概率和。
在查找所有正确预测序列时,采用了前向后向算法。
前向过程计算从1-t时刻,预测出正确的前缀的概率;后向过程计算从t - T时刻,预测出正确的后缀的概率。
那么: 前缀概率 * 后缀概率 / t 时刻预测s的概率 = t 时刻时所有正确的预测序列的概率。
动态规划降低时间复杂度:只有在前一时刻到达预测出某些特定符号,在当前时刻,才可以做出正确预测。
那么,到 t 时刻为止,预测出正确的 标签序列的前缀 的概率 = (到t - 1为止预测正确的所有子序列概率和) * 预测出当前标签的概率。
定义与背景
CTC全称:Connectionist temporal classification, 主要用于处理序列标注问题中的输入与输出标签的对齐问题。
--------------------------------
什么是数据的对齐问题? (参考链接:https://www.cnblogs.com/qcloud1001/p/9041218.html)
传统的语音识别的声学模型训练,对于每一帧的数据,需要知道对应的label才能进行有效的训练,在训练数据之前需要做语音对齐的预处理。
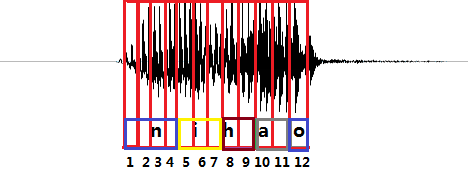
上图是“你好”这句话的声音的波形示意图, 每个红色的框代表一帧数据,传统的方法需要知道每一帧的数据是对应哪个发音音素。比如第1,2,3,4帧对应n的发音,第5,6,7帧对应i的音素,第8,9帧对应h的音素,第10,11帧对应a的音素,第12帧对应o的音素。(这里暂且将每个字母作为一个发音音素)
------------------------------------
传统模型的不足:
1. 训练数据之前需要做语音对齐的预处理,工作比较耗时,并且在缺失对齐标签时,无法做出准确预测;
2. 输出的预测是局部分类,只利用了当前帧的信息,并未利用序列的全局信息(比如相邻两个标签的连续性等,则需要通过其他外加处理。)
------------------------------------------
CTC与传统模型的对比:
1. 与传统的声学模型训练相比,采用CTC作为损失函数的声学模型训练,是一种完全端到端的声学模型训练,不需要预先对数据做对齐,只需要一个输入序列和一个输出序列即可以训练。这样就不需要对数据对齐和一一标注,输入输出之间的alignment不再那么重要。
2. CTC直接输出序列预测的概率,不需要外部的后处理。
--------------------------------------------
CTC的算法原理
<1> 符号定义与目标函数
1. $A$: 序列标注任务中的标签所在字母表集合为 $A$
2. $A'$: 扩展的字母表集合。CTC的softmax 输出层中,比 $A$ 多包含一个标签。我们记为$'blank'$. 即 $A' = A \bigcup \{blank\}$. 那么在输出预测时,前$|A|$个单元输出的是对应字母表$A$中各元素的预测概率,最后一个单元输出的是预测为$'blank'$的概率。
3. $y_k^t$: 网络在 $t$ 时刻输出元素 $k$ 的概率,即在给定长度为 $T$ 的输入序列 $x$ 后,在 $t$ 时刻,预测为 $A'$ 中的元素 $k$ 的概率。
4. $A^{'T}$: 在 $A'$ 集合上的所有长度为 $T$ 的序列集合。
5. 假设在每一个时刻的输出与其他时刻的输出是条件独立的(或者说,条件独立于给定的 $x$ ),那么可以得到在给定输入 $x$ 后,得到 $A^{'T}$ 集合中任何一条路径 $\pi$ 的概率分布: $ \pi \in A^{'T}$ 的分布:
$$p(\pi | x) = \prod_{t = 1} ^ T y_{\pi_t}^t \tag1$$ 。
我们记在$A^{'T}$集合中的序列 $\pi$ 为 $paths$.
6. $l$: 我们记在 $A$ 集合中产生的标签序列为 $l$。
7. 由于在$A^{'T}$ 集合中可能有多条 $paths$,最终所映射的都是同一个序列, 我们需要定义一个多对一的函数,来实现从 $paths$集合到预测序列的映射。$F: A^{'T} \rightarrow A^{\le T}$
其中,我们设定映射后的序列长度不大于映射前的序列长度。
这是要做什么呢?举个例子:
$F(a-ab-) = F(-aa--abb) = aab$
函数映射关系是,将'-'与'-'之间的重复的元素,只保留一个,并且去掉'-'分隔。这样,无论我们的神经网络预测出的序列为‘a-ab-’ 或是 ‘-aa--abb’,它所对应的最终的预测结果都是 'aab',而我们的目标函数也是将 'aab' 与真实标签序列作比较。
这样就不难看出,CTC算法并不要求预测标签与输入的一一对齐关系,而是关注于整个序列的最终预测结果,也就是经过这个函数映射后的结果。
那么我们预测出真实标签序列的概率可以表示为:
$$ p(l|x) = \sum_{\pi \in F^{-1}(l)} p(\pi|x) \tag2$$
即所有的可以映射为真实标签序列的 预测序列的概率和。
<2> blank标签的角色
1. 可以出现重复字符。
设想一下,如果没有'-',对于单词中有重复字符的,比如'apple',其函数映射的结果为'aple',这是不能满足实际情况需要的
2. 如果没有'-',那么神经网络需要一直不停的预测出来一个label,直到下一个不同的label出现。而真实情况中,经常出现一段间隔内(比如语音的停顿处),并没有标签。所以有blank可以满足这样的情况需要。
<3> 前向后向算法的前向过程
由公式(2),我们的目标函数是对所有可以映射为真实标签序列的paths的预测出的概率求和。那么首先,我们要先知道都有哪些paths可以映射为真实标签序列。
对于长度为 $T$ 的输入序列和长度为 $U$ 的标签序列,有 $2^{T - U^2 + U(T - 3)} * 3 ^ {(U - 1)(T - U) - 2}$ 种不同的paths.
显然,这是指数级别的复杂度,不能满足实际需要。为了降低时间复杂度,CTC算法处理时采用了动态规划方法。算法的主要思想是,在筛选可能的paths时,只选取前缀与$l$对应前缀是相同的那些paths. 这样说很难理解,举个例子。
1. 首先,我们构造一个table,希望通过这个table,直观的看出所有可以映射到真实标签序列'apple'的可能路径。
table的横坐标为输入的时间序列,纵坐标为将真实标签序列两两字母以'-'分隔,并且在首尾各加一个'-'。
那么从首'-'或'a'开始,到尾'e'或'-'结束;箭头只能向右,或向下,所有依次经过a, p, p, l, e的那些路径,即为我们要找的,可以映射为真实标签序列的路径。
比如下图1,黑线部分表示的预测的序列为 '- - a p - p l- e' (t1时刻预测'-', t2时刻预测为'-', t3时刻预测为'a' ...)。 注意,红色箭头是错误的,因为我们不可能先预测出第3个标签,再预测出第2个标签,标签需要按顺序依次预测出。所以,箭头只能向右或向下!$F( '- - a p - p l- e') = 'apple'$
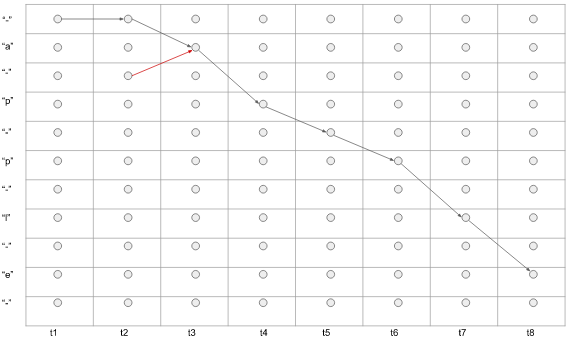
图1.路径举例
那么初始t1时刻,我们只能处于'-'或‘a’的位置,
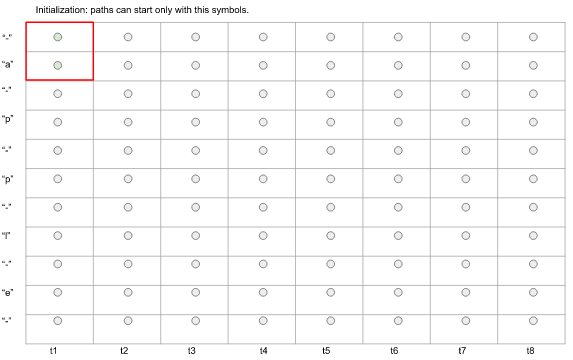
图2. 初始时刻状态
而最终,我们需要依次经过apple所有字母。
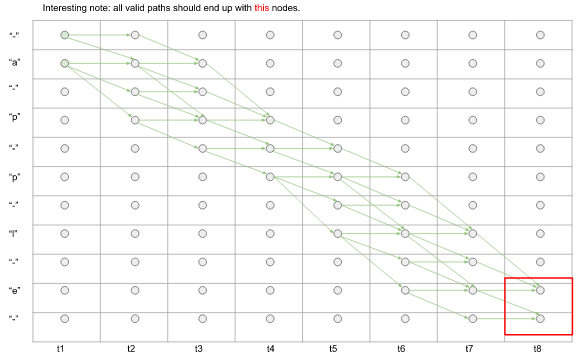
图3.搜索的最终结果状态。
那么,求总路径的问题,也就是找从初始位置,到结束位置的所有的可能路径的问题。
动态规划体现在哪里呢?敲黑板,下面内容是重点~
(1) 对于一条可能路径,其字路径的概率可以表示为,对应时刻神经网络预测标签的概率乘积。比如,如下图所示 $p('- a p - ') = y_-^1 * y_a ^ 2 * y_p^3 * y_-^4$
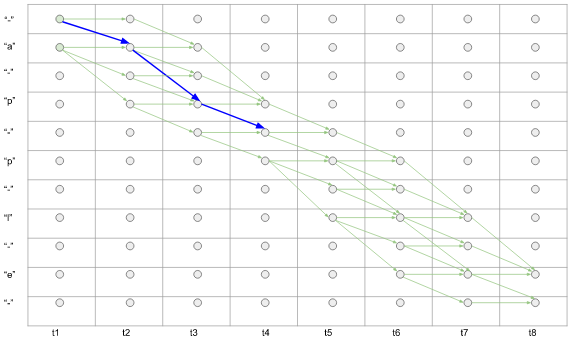
图4. subpath的概率计算
(2) $\alpha_t(s)$: 称为前向变量(forward variable)。表示 前缀末端 在 $t$ 时刻到达序列的第 $s$ 个位置的所有可能子路径的概率和。前缀的意义是,在前$(1-t)$时间内,经过映射后,可以得到真实标签序列的前s / 2个符号。我们把符合这个要求的所有可能路径前缀的概率加和,即为 $\alpha_t(s)$。
那么以此类推,在T时刻,可以到达终止节点'-',或真实标签最后一个符号的,概率和,即为所有可以映射得到真实标签序列的预测序列的概率和,也就是我们需要最大化的目标。
如下图5所示:在 $t3$ 时刻,共有四条路径前缀终止于扩展的标签序列的的第4个节点p.那么$\alpha_3(4) = p('-ap') + p('aap') + p('a-p') + p('app')$ 这四条子路径的前缀经过映射后,都可以得到真实标签序列的前缀:'ap'.
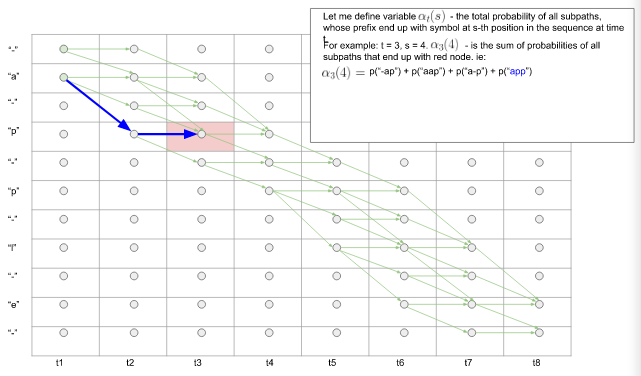
图5.前缀相同的子路径的概率和
(3) 之后,我们需要做的就是,对于每一个cell,都计算其对应的 $\alpha_t(s)$。我们可以递归地进行计算。
即计算可以到达(t, s) 这个cell 的所有子路径概率和 与 在t时刻预测出符号s的概率做乘积,即为在t时刻,到达符号s的所有子路径的概率。
在计算中,有三种情况:
Case1. 第 $s$ 个符号为blank时。
比如 $s = 3, t = 3$,序列的第三个符号为 '-'。见图中红色的cell. $\alpha_3(3)$ 只取决于 $\alpha_2(3)$ (蓝色cell)和 $\alpha_2(2)$ (绿色cell). 那么易得,$\alpha_3(3) = (\alpha_2(3) + \alpha_2(2)) * y_-^3$.
一般的,有$$\alpha_t(s) = (\alpha_{t-1}(s) + \alpha_{t-1}(s-1)) * y_{seq(s)}^t \tag3$$
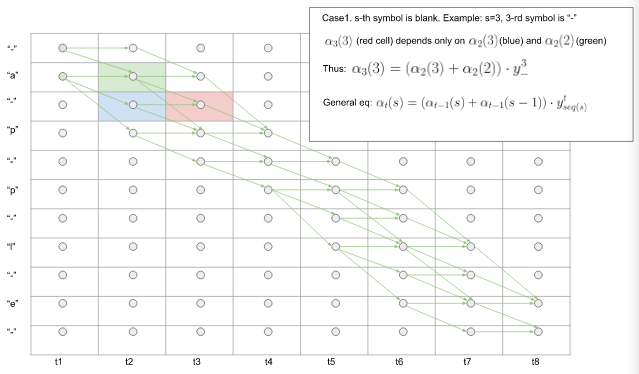
图6. Case1.前向算法中s=‘-’时的$\alpha_s^t$ 计算
Case2. 第s个符号与第(s - 2)个符号相同时,即$seq(s) == seq(s - 2) $。
此时(t,s)cell,只取决于 (t-1, s) (蓝色cell) 和 (t - 1, s - 1)(绿色cell)。一般的:
$$\alpha_t(s) = (\alpha_{t-1}(s) + \alpha_{t-1}(s-1)) * y_{seq(s)}^t \tag4$$
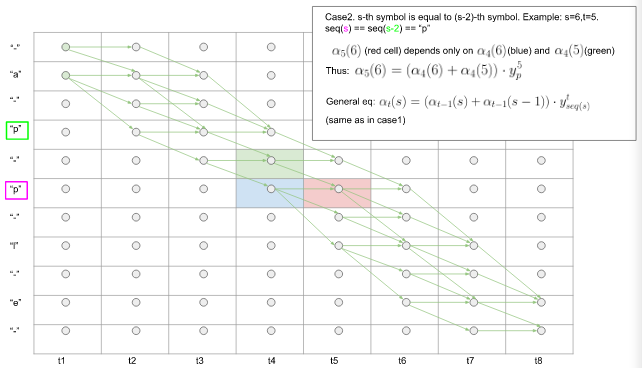
图7. Case2.前向算法中seq(s) == seq(s - 2)时的$\alpha_s^t$ 计算
Case3. 其他情况。有:
$$\alpha_t(s) = (\alpha_{t-1}(s) + \alpha_{t-1}(s-1) + \alpha_{t-1}(s-2) ) * y_{seq(s)}^t \tag5$$
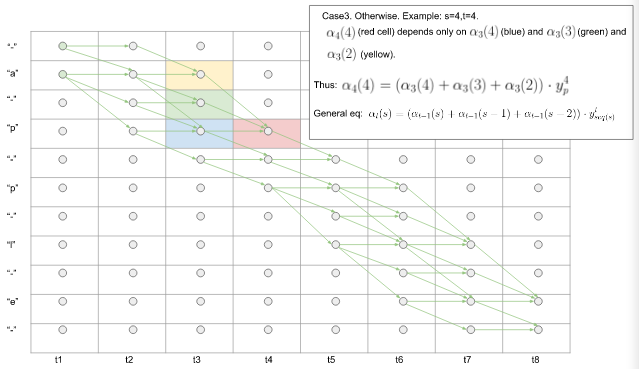
图8. Case3.前向算法中其他情况下 $\alpha_s^t$ 的计算
(4) 通过以上步骤,我们最终可以得到$\alpha_T(U - 1)$ 和 $\alpha_T(U)$。那么预测出真实标签序列的概率为 $$p(l|x) =\alpha_T(U - 1) + \alpha_T(U) \tag6 $$. 前向过程完成!
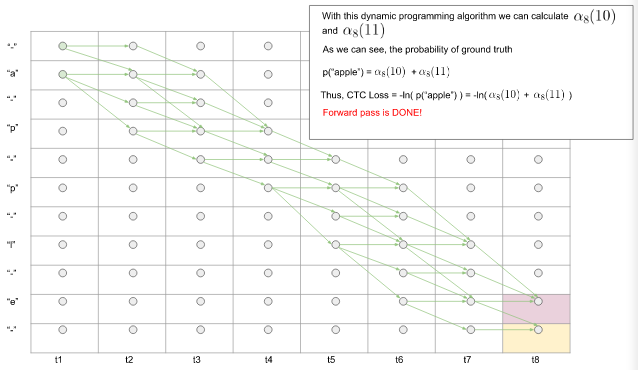
图9. 前向过程完成得到预测出真实序列的概率
<4> 前向后向算法的后向过程
后向算法与前向类似,只是方向不同,后向是找 从序列末端到首端的各个子路径的概率。
定义$\beta_t(s)$为 后缀起始于序列末端, $t$ 时刻到达第 $s$ 个符号的所有可能子路径的概率和。
比如,$t = 6, s = 8, \beta_6(8)$表示所有以下图中红色节点开始的,最终可以到达序列末端的子路径的概率。$\beta_6^(8) = p('lle') + p('l-e') + p('lee') + p('le')$

图10. 反向过程举例
那么,将前向过程中所有箭头反向,使用同样的计算方式,即可计算出反向变量。
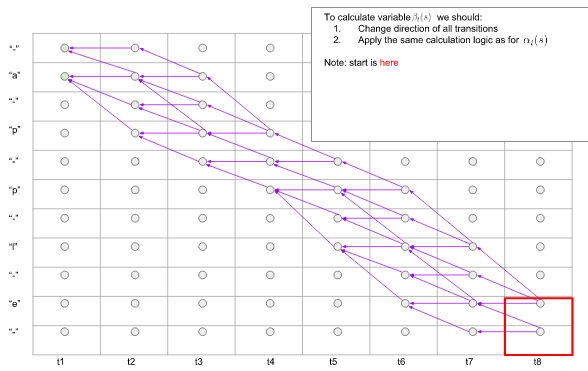
图10. 反向过程
<5> 前向后向算法
<3>部分$\alpha_s(t)$前向变量记录1-t时间内预测出正确前缀的概率(或者可以说,子路径的概率和);<4>部分$\beta_s(t)$后向变量记录t - T时间内预测出正确后缀的概率;
那么
$$\alpha_s(t) * \beta_s(t) / y_t^s\tag7$$
即为 在t时刻,所有正确预测的,并且经过第s符号的,路径的概率和。(除以 y_t^s 因为在 $\alpha$ 和 $\beta$ 中乘了两次)。
举个例子:
$\alpha_t3(2) = y_-^{t1} * y_-^{t2} * y_a^{t3} + y_-^{t1} * y_-^{t2} * y_-^{t3}$
$\beta_t3(2) = y_a^{t3} * y_p^{t4} * y_-^{t5} * y_p^{t6} * y_l^{t7} * y_e^{t8}$
$\alpha_t3(2) * \beta_t3(2) = ( y_-^{t1} * y_-^{t2} * y_a^{t3} ) * ( y_a^{t3} * y_p^{t4} * y_-^{t5} * y_p^{t6} * y_l^{t7} * y_e^{t8}) + (y_-^{t1} * y_-^{t2} * y_-^{t3}) * (y_a^{t3} * y_p^{t4} * y_-^{t5} * y_p^{t6} * y_l^{t7} * y_e^{t8}) = (p('--ap-ple') + p('-aap-ple) + p('aaap-ple')) * y_a^3$
那么 $\alpha_t3(2) * \beta_t3(2) / y_a^3$ = 在t3时刻,经过符号a的所有正确预测序列的概率和。

图11. 前向后向算法,在t时刻经过第s符号的所有正确预测的路径的概率和
那么将t3时刻,正确预测序列可能会预测出,a, -, p, -,用上面方法,将经过这四个符号的路径概率加和,即可得到在t3时刻,可以做出正确预测的概率。
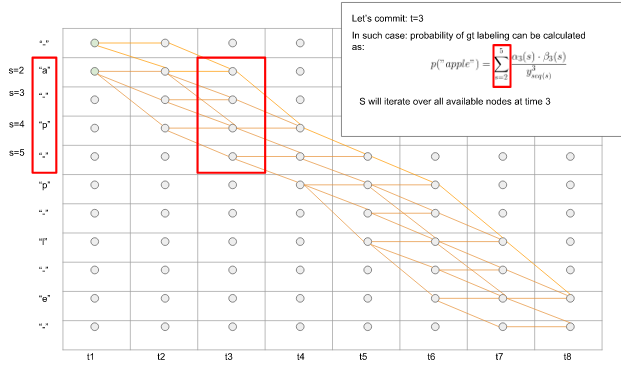
图11. 前向后向算法,在t时刻可以做出正确预测的概率
最后,应用于1 - T的所有时刻,可以得到在任意时刻内预测出正确标签序列的概率。
$$p('apple') = \sum_{s = 1}^{|seq|} \frac{\alpha_s(t) * \beta_s(t)}{y_{seq(s)} ^ t}\tag8$$
<6> 反向传播
我们的目标是最大化$p('apple')$,也就是$ min {-ln(p('apple'))}$,这是我们的目标函数
在反向传播时,我们需要对神经网络的每一个预测输出求偏导。
$$\frac{\partial{(-ln(p('apple')))}}{\partial{y_k^t}} = -\frac{1}{p('apple')} * \frac{\partial{p('apple')}}{\partial{y_k^t}}\tag9$$
我们重点看$\frac{\partial{p('apple')}}{\partial{y_k^t}} \tag{10}$的求解。
$\frac{ \partial{p('apple')} } {\partial{y_k^t} } = \frac{\alpha_{s1}(t) * \beta_{s1}(t)}{y_{s1}^t} + ... + \frac{\alpha_{k}(t) * \beta_{s1}(t)}{y_{k}^t} +... + \frac{\alpha_{sT}(t) * \beta_{sT}(t)}{y_{sT}^t}$
若t时刻过k,则t时刻时不可能经过其他字符的。也就是,在求偏导时,只有红色部分是包含$y_k^t$的,其他项可以看做常数项。
最终,
$$\frac{ \partial{p('apple')} } { \partial{y_k^t} } = -\frac{1}{{y_k^t}^2} * \sum_{s:seq(s) = k}\alpha_t(s) * \beta_t(s)\tag{11}$$
举个例子:

这样就完成了!
------------------------------------------
思考:
$\alpha_S(T)$即可可表示所有正确预测序列的概率和,也就是可以表示目标函数,为什么要引入$\beta$呢?
原因:为了反向传播时候求偏导方便呀!否则$\alpha_S(T)$是关于$y_k^t$的一个复杂的函数,很难直接求导的,引入$\beta$后,我们可以关注于t时刻内的偏导计算,会简便许多。
------------------------------------------
<7> 要点总结
1. 动态规划
2. 矩阵 $\alpha$ (前向变量)用于计算loss.
3. 矩阵$\beta$ (后向变量)用来方便计算gradients.
=======================================


感谢您的打赏!
(梦想还是要有的,万一您喜欢我的文章呢)
CTC (Connectionist Temporal Classification) 算法原理的更多相关文章
- CTC(Connectionist Temporal Classification)介绍
CTC解决什么问题 CTC,Connectionist Temporal Classification,用来解决输入序列和输出序列难以一一对应的问题. 举例来说,在语音识别中,我们希望音频中的音素和翻 ...
- 梯度迭代树(GBDT)算法原理及Spark MLlib调用实例(Scala/Java/python)
梯度迭代树(GBDT)算法原理及Spark MLlib调用实例(Scala/Java/python) http://blog.csdn.net/liulingyuan6/article/details ...
- DQN算法原理详解
一. 概述 强化学习算法可以分为三大类:value based, policy based 和 actor critic. 常见的是以DQN为代表的value based算法,这种算法中只有一个值函数 ...
- Bagging与随机森林算法原理小结
在集成学习原理小结中,我们讲到了集成学习有两个流派,一个是boosting派系,它的特点是各个弱学习器之间有依赖关系.另一种是bagging流派,它的特点是各个弱学习器之间没有依赖关系,可以并行拟合. ...
- RSA算法原理
一直以来对linux中的ssh认证.SSL.TLS这些安全认证似懂非懂的.看到阮一峰博客中对RSA算法的原理做了非常详细的解释,看完之后茅塞顿开,关于RSA的相关文章如下 RSA算法原理(一) RSA ...
- LruCache算法原理及实现
LruCache算法原理及实现 LruCache算法原理 LRU为Least Recently Used的缩写,意思也就是近期最少使用算法.LruCache将LinkedHashMap的顺序设置为LR ...
- MySQL索引背后的数据结构及算法原理【转】
本文来自:张洋的MySQL索引背后的数据结构及算法原理 摘要 本文以MySQL数据库为研究对象,讨论与数据库索引相关的一些话题.特别需要说明的是,MySQL支持诸多存储引擎,而各种存储引擎对索引的支持 ...
- OpenGL学习进程(13)第十课:基本图形的底层实现及算法原理
本节介绍OpenGL中绘制直线.圆.椭圆,多边形的算法原理. (1)绘制任意方向(任意斜率)的直线: 1)中点画线法: 中点画线法的算法原理不做介绍,但这里用到最基本的画0<=k ...
- 支持向量机原理(四)SMO算法原理
支持向量机原理(一) 线性支持向量机 支持向量机原理(二) 线性支持向量机的软间隔最大化模型 支持向量机原理(三)线性不可分支持向量机与核函数 支持向量机原理(四)SMO算法原理 支持向量机原理(五) ...
随机推荐
- 一点一点看JDK源码(六)java.util.LinkedList前篇之链表概要
一点一点看JDK源码(六)java.util.LinkedList前篇之链表概要 liuyuhang原创,未经允许禁止转载 本文举例使用的是JDK8的API 目录:一点一点看JDK源码(〇) 1.什么 ...
- Oracle中转义下划线
原意是查询出所有的月粒度模型,但是在oracle中,下划线也代表匹配单一任何字符,导致15分钟粒度的模型也被查询出来,在此,需要对下划线做转义,使其只表示下划线的含义,可以使用ESCAPE()函数. ...
- 05 oracle中lock和latch的用途
oracle中lock和latch的用途 本文向各位阐述Oracle的Latch机制,Latch,用金山词霸翻译是门插栓,闭锁,专业术语叫锁存器,我开始接触时就不大明白为什么不写Lock,不都是锁 ...
- 技巧:Vimdiff 使用(改)
技巧:Vimdiff 使用(改) 各种 IDE 大行其道的同时,传统的命令行工具以其短小精悍,随手可得的特点仍有很大的生存空间,这篇短文介绍了一个文本比较和合并的小工具:vimdiff.希望能对在 U ...
- nopCommerce电子商务平台 安装教程(图文)
nopCommerce是一个通用的电子商务平台,适合每个商家的需要:它强大的企业和小型企业网站遍布世界各地的公司销售实体和数字商品.nopCommerce是一个透明且结构良好的解决方案,它结合了开源和 ...
- #leetcode刷题之路35-搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引.如果目标值不存在于数组中,返回它将会被按顺序插入的位置.你可以假设数组中无重复元素. 示例 1:输入: [1,3,5,6], 5输出: ...
- LeetCode 中级 -二叉树的层次遍历(102)
题目描述: 给定一个二叉树,返回其按层次遍历的节点值. (即逐层地,从左到右访问所有节点). 例如:给定二叉树: [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 ...
- CF1066D Boxes Packing(二分答案)
题意描述: 你有$n$个物品,每个物品大小为$a_i$,$m$个盒子,每个盒子的容积为$k$.$Maksim$先生想把物品装入盒子中.对于每个物品,如果能被放入当前的盒子中,则放入当前盒子,否则换一个 ...
- 806. Number of Lines To Write String (5月24日)
解答 class Solution { public: vector<int> numberOfLines(vector<int>& widths, string S) ...
- 「PHP」策略模式
引言 所属:行为型模式,常用设计模式之一 学习资料: <大话设计模式>程杰 模式概述 分享一篇关于策略模式讲的很好的文章,大家可以参考一下:https://www.cn ...
