GCJ2008 APAC local onsites C Millionaire

自己Blog的第一篇文章，嗯...

接触这道题，是从《挑战程序设计竞赛》这本书看来的，其实头一遍读题解，并没有懂。当然现在已经理解了，想想当初可能是因为考虑两轮的那张概率图的问题。于是决定把自己的理解整理一下。

题面

（喜欢看原题的同学！这里来！GCJ官网直接配送哦！）

Problem

You have been invited to the popular TV show "Would you like to be a millionaire?". Of course you would!

The rules of the show are simple:

• Before the game starts, the host spins a wheel of fortune to determine P, the probability of winning each bet.
• You start out with some money: X dollars.
• There are M rounds of betting. In each round, you can bet any part of your current money, including none of it or all of it. The amount is not limited to whole dollars or whole cents.

  If you win the bet, your total amount of money increases by the amount you bet. Otherwise, your amount of money decreases by the amount you bet.

• After all the rounds of betting are done, you get to keep your winnings (this time the amount is rounded down to whole dollars) only if you have accumulated $1000000 or more. Otherwise you get nothing.

Given M, P and X, determine your probability of winning at least $1000000 if you play optimally (i.e. you play so that you maximize your chances of becoming a millionaire).

Answers with a relative or absolute error of at most 10^-6 will be considered correct.

Limits

1 ≤ N ≤ 100
0 ≤ P ≤ 1.0, there will be at most 6 digits after the decimal point.
1 ≤ X ≤ 1000000

Small dataset

1 ≤ M ≤ 5

Large dataset

1 ≤ M ≤ 15

题意

你被邀请去玩一个赌博游戏。一开始你有美刀X，接着进行M轮赌博。每一轮你可以拿出自己的一部分钱作为赌注，可以不是整数。当然，你也可以选择全押或者不押都可以。每一轮有P的概率你会赢，赢了赌注就会翻倍，输了赌注就没有了。最后你如果持有1 000 000美刀以上的钱的话，就可以把这些钱带回家。请计算当你采取最优策略时，获得1 000 000美刀以上并带回家的概率。

§ 1 难点

你会十分绝望的发现，每轮当前的钱和赌注都可以是小数，这直接使得暴力枚举的方法无用。

§ 2 离散化！

我们先从简单入手，分析一下最后一轮下会出现的情况。

• 如果你持有$1 000 000及以上的钱，那这轮就没必要赌了，因为你可以保证你有1的概率把钱带回家。
• 如果你持有$500 000及以上的钱，那不妨全押上。这样你有P的概率，可以让手头的钱翻倍，那就超过$1 000 000，可以带回家了。但若你不全押，赢了却不一定能达到$1 000 000，输了就是肯定带不回去的（所以输的情况其实和全押是一样的）。因而全押更划得来， 有P的概率可以带回家。
• 如果你持有不到$500 000，即使这一轮你全押并且赢了，也达不到$1 000 000。有0的概率可以带回家。

这样一共是三种情况。你会发现，即使当前持有金额它可能是小数，但是在一段段连续的区间里，带回家的概率都是一样的，这样我们就把当前你持有的金额这个无限的空间，映射到三段简单易见的范围中去了，达到了离散化的效果。

同样，最后两轮时，我们会分为五种情况考虑：0 ~ $250 000, $250 000 ~ $500 000, $500 000 ~ $750 000, $750 000 ~ $1 000 000, $1 000 000 ~ +INF

为什么是这样呢？

我们这个时候可以先列出一个递推式：

• Probability(next round)_sum = max{ P * Probability(this round)_{sum + stake} + (1 - P) * Probability(this round)_{sum - stake} }
• 其中 Probability_sum 表示某一轮开始手头持有金额为sum的概率，stake表示当前这一轮的赌注。

这个式子就不必解释了，接下来我们看下面一张图。

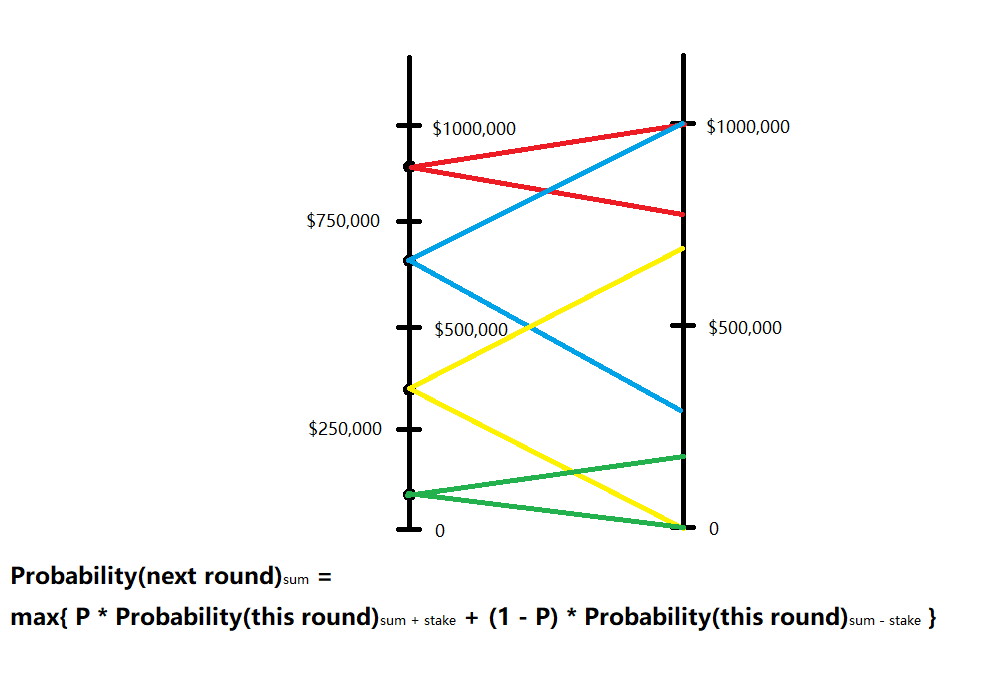
• 它就是按照我们当前的例子画的，左边线段表示最后两轮概率的情况，右边线段表示最后一轮概率的情况。不同的颜色的线在右边线段上框出的范围表示左边线段上的点按照上式计算概率时会涉及到的范围。
• 注意到边界0和$1000 000（超过$1000 000概率为1，没有必要研究），这个范围是不能超过边界的。
• 并且，左边线段上我们多取了两个点，是右边线段相邻两个点的中点。

你会发现，右边线段 0 ~ $1 000 000 这个区间被分为四段，而这四段可以涉及到的范围都是不相同的。比如说 $750 000 ~ $1 000 000 这段最多能涉及到最后一轮时 $500 000 ~ $1 000 000 的范围，而 $500 000 ~ $750 000 涉及可以涉及到最后一轮 0 ~ $1000 000 的范围。（可以多画几个点看一看）

显然这四段同一段里面的点概率都是相同的。

因此最后两轮被分为了5种情况。

所以说，最后M轮的时候，会被分为(2^M+1)种情况。且每次多增加的情况间的分界点就是上一轮两个分界点的中点。

这样就只需要考虑这(2^M+1)种情况就可以了，于是达到了离散化的效果。

§ 3 参考代码

就是《挑战》里的写法，已经在GCJ上通过了Small和Large的。（就是Large实在跑得有点慢，不过没有Time Limit）

// Millionaire
// GCJ 2008 APAC local onsites C

#include <cstdio>
#include <cstring>
#include <algorithm>
const int MAXR =  <<  + ;
int N, M, X;
double P, dp[][MAXR];

int main() {
    freopen("C-large-practice.in", "r", stdin);
    freopen("C-answer.out", "w", stdout);
    scanf("%d", &N);
    int i, k, j, l, r;
    for (k = ; k <= N; k++) {
        scanf("%d%lf%d", &M, &P, &X);
        r =  << M;
        double *prv = dp[], *nxt = dp[];
        memset(prv, , sizeof(double) * (r + ));
        prv[r] = 1.0;
        for (i = ; i < M; i++) {
            for (j = ; j <= r; j++) {
                int Lim = std::min(j, r - j);
                nxt[j] = 0.0;
                for (l = ; l <= Lim; l++) nxt[j] = std::max(nxt[j], P * prv[j + l] + ( - P) * prv[j - l]);
            }
            std::swap(prv, nxt);
        }
        i = (long long)X * r / ;
        printf("Case #%d: %.6lf\n", k, prv[i]);
    }
    fclose(stdin);
    fclose(stdout);
　　 return 0;
}

另外，有问题的童鞋欢迎提问~

谢谢大家！