hdu 3435(KM算法最优匹配)

A new Graph Game

Time Limit: 8000/4000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2360    Accepted Submission(s): 951

Problem Description

An
undirected graph is a graph in which the nodes are connected by
undirected arcs. An undirected arc is an edge that has no arrow. Both
ends of an undirected arc are equivalent--there is no head or tail.
Therefore, we represent an edge in an undirected graph as a set rather
than an ordered pair.
Now given an undirected graph, you could delete
any number of edges as you wish. Then you will get one or more
connected sub graph from the original one (Any of them should have more
than one vertex).
You goal is to make all the connected sub graphs
exist the Hamiltonian circuit after the delete operation. What’s more,
you want to know the minimum sum of all the weight of the edges on the
“Hamiltonian circuit” of all the connected sub graphs (Only one
“Hamiltonian circuit” will be calculated in one connected sub graph!
That is to say if there exist more than one “Hamiltonian circuit” in one
connected sub graph, you could only choose the one in which the sum of
weight of these edges is minimum).
  For example, we may get two possible sums:

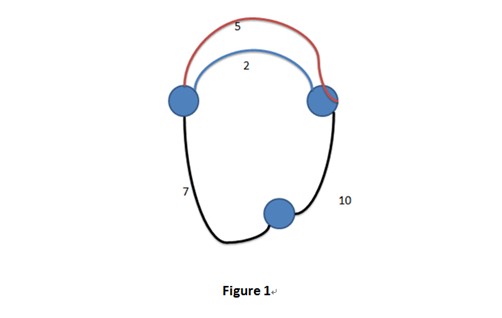
(1)  7 + 10 + 5 = 22
(2)  7 + 10 + 2 = 19
(There are two “Hamiltonian circuit” in this graph!)

 

Input

In the first line there is an integer T, indicates the number of test cases. (T <= 20)
In
each case, the first line contains two integers n and m, indicates the
number of vertices and the number of edges. (1 <= n <=1000, 0
<= m <= 10000)
Then m lines, each line contains three integers
a,b,c ,indicates that there is one edge between a and b, and the weight
of it is c . (1 <= a,b <= n, a is not equal to b in any way, 1
<= c <= 10000)

 

Output

Output
“Case %d: “first where d is the case number counted from one. Then
output “NO” if there is no way to get some connected sub graphs that any
of them exists the Hamiltonian circuit after the delete operation.
Otherwise, output the minimum sum of weight you may get if you delete
the edges in the optimal strategy.

 

Sample Input

3

3 4
1 2 5
2 1 2
2 3 10
3 1 7

3 2
1 2 3
1 2 4

2 2
1 2 3
1 2 4

 

Sample Output

Case 1: 19
Case 2: NO
Case 3: 6

 

题意:将一个无向图删边得到一些子图，并使每个子图中存在哈密顿回路，并使所有哈密顿回路上边的权值最小。如果有,输出这个最小的子图,如果没有,输出NO。

题解:每个点的话就是出度和入度都为1了,每个点必须且仅走一次，这样的话就是二分图完美匹配了。

#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int INF = ;
const int N = ;
int graph[N][N];
int lx[N], ly[N];
bool visitx[N], visity[N];
int slack[N];
int match[N];
int n,m;
bool Hungary(int u)
{
    int temp;
    visitx[u] = true;
    for(int i = ; i <= n; ++i)
    {
        if(visity[i])
            continue;
        else
        {
            temp = lx[u] + ly[i] - graph[u][i];
            if(temp == ) //相等子图
            {
                visity[i] = true;
                if(match[i] == - || Hungary(match[i]))
                {
                    match[i] = u;
                    return true;
                }
            }
            else //松弛操作
                slack[i] = min(slack[i], temp);
        }
    }
    return false;
}
void KM()
{
    int temp;
    memset(match,-,sizeof(match));
    memset(ly,,sizeof(ly));
    for(int i = ;i <= n;i++) //定标初始化
        lx[i] = -INF;
    for(int i =;i<=n;i++)
        for(int j=;j<= n;j++)
            lx[i] = max(lx[i], graph[i][j]);
    for(int i = ; i <= n;i++)
    {
        for(int j = ; j <= n;j++)
            slack[j] = INF;
        while()
        {
            memset(visitx,false,sizeof(visitx));
            memset(visity,false,sizeof(visity));
            if(Hungary(i))
                break;
            else
            {
                temp = INF;
                for(int j = ; j <= n; ++j)
                    if(!visity[j]) temp = min(temp, slack[j]);
                for(int j = ; j <= n; ++j)
                {
                    if(visitx[j]) lx[j] -= temp;
                    if(visity[j]) ly[j] += temp;
                    else slack[j] -= temp;
                }
            }
        }
    }
}
int main()
{
    int tcase;
    int t= ;
    scanf("%d",&tcase);
    while(tcase--){
        scanf("%d%d",&n,&m);
        for(int i=;i<=n;i++){
            for(int j=;j<=n;j++){
                graph[i][j] = -INF;
            }
        }
        for(int i=;i<=m;i++){
            int u,v,w;
            scanf("%d%d%d",&u,&v,&w);
            if(u==v) continue;
            graph[u][v] = graph[v][u] = max(graph[u][v],-w);
        }
        KM();
        int ans = ;
        bool flag = false;
        for(int i=;i<=n;i++){
            if(match[i]==-||graph[match[i]][i]==-INF){
                flag = true;
                break;
            }
            ans+=graph[match[i]][i];
        }
        printf("Case %d: ",t++);
        if(flag)printf("NO\n");
        else printf("%d\n",-ans);
    }
    return ;
}