协方差Covariance的表述推导
今天想了一下关于概率论的一维数据期望、方差以及高维数据的矩阵表示,突然想到为什么在一维中
方差的表示为:V(x) = E((x-E(x))2)
而到了高维,这样的表述就成了协方差呢?V(X) = E((X-µ)(X-µ)T), 它为什么可以表示协方差呢?于是拿出笔自己推到了一下,果然!
详细推导过程见下图:
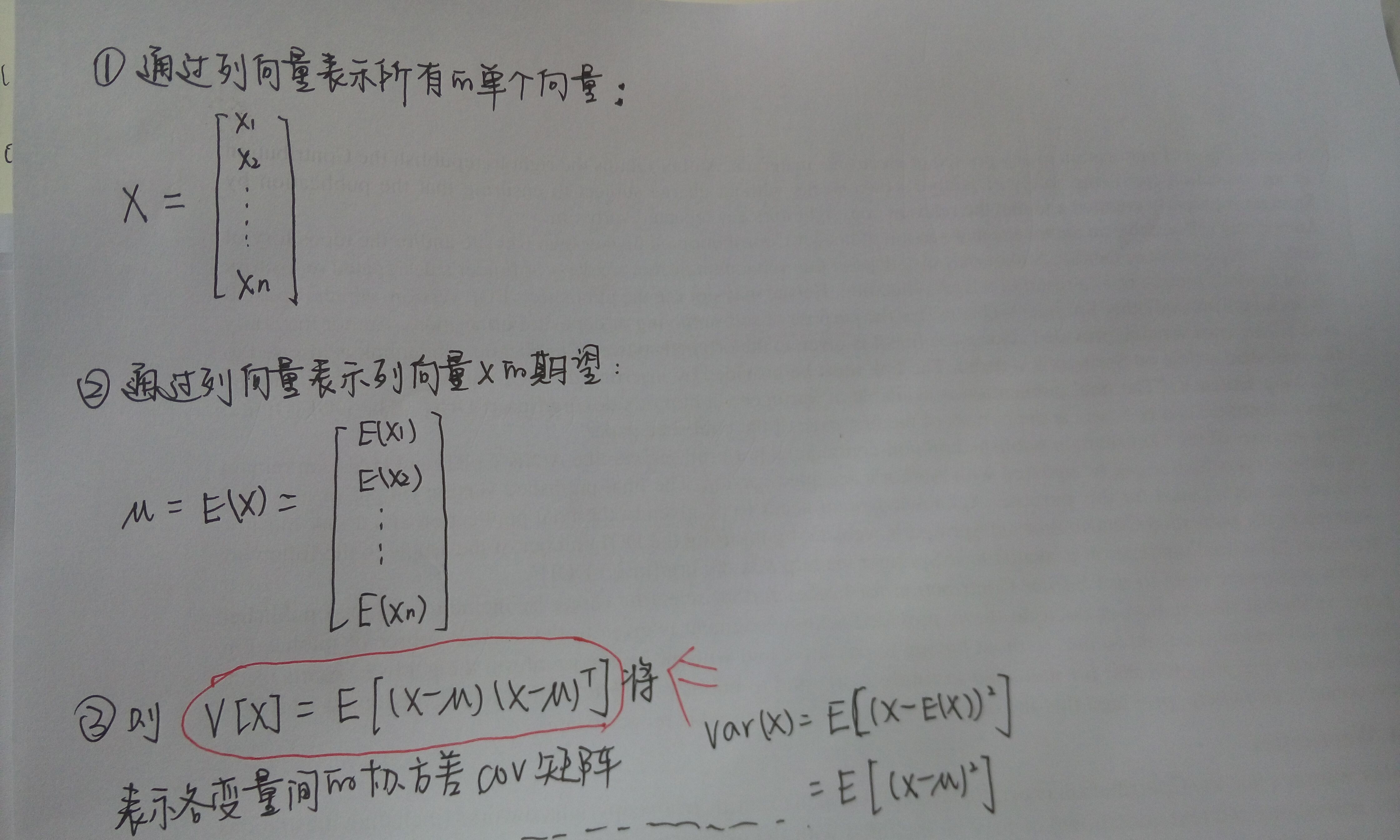

所以,我们可以得出 V(X) = E((X-µ)(X-µ)T) 其实就是描述了变量之间的协方差,就是协方差矩阵。
协方差Covariance的表述推导的更多相关文章
- 方差variance, 协方差covariance, 协方差矩阵covariance matrix
https://www.jianshu.com/p/e1c8270477bc?utm_campaign=maleskine&utm_content=note&utm_medium=se ...
- 方差variance, 协方差covariance, 协方差矩阵covariance matrix | scatter matrix | weighted covariance | Eigenvalues and eigenvectors
covariance, co本能的想到双变量,用于描述两个变量之间的关系. correlation,相关性,covariance标准化后就是correlation. covariance的定义: 期望 ...
- 【概率论】4-6:协方差和相关性(Covariance and Correlation)
title: [概率论]4-6:协方差和相关性(Covariance and Correlation) categories: - Mathematic - Probability keywords: ...
- 学习笔记DL008:概率论,随机变量,概率分布,边缘概率,条件概率,期望、方差、协方差
概率和信息论. 概率论,表示不确定性声明数学框架.提供量化不确定性方法,提供导出新不确定性声明(statement)公理.人工智能领域,概率法则,AI系统推理,设计算法计算概率论导出表达式.概率和统计 ...
- Python3Numpy——相关性协方差应用
基本理论 Correlation Are there correlations between variables? Correlation measures the strength of the ...
- Reading | 《DEEP LEARNING》
目录 一.引言 1.什么是.为什么需要深度学习 2.简单的机器学习算法对数据表示的依赖 3.深度学习的历史趋势 最早的人工神经网络:旨在模拟生物学习的计算模型 神经网络第二次浪潮:联结主义connec ...
- PCA原理分析
动机 在机器学习领域中,我们常常会遇到维数很高的数据,有些数据的特征维度高达上百万维,很显然这样的数据是无法直接计算的,而且维度这么高,其中包含的信息一定有冗余,这时就需要进行降维,总的来说,我们降维 ...
- [转]概率基础和R语言
概率基础和R语言 R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大. R语言作为统计学一门语言,一直在小众领域闪耀着光芒.直到大数据的爆发,R语 ...
- Python 主成分分析PCA
主成分分析(PCA)是一种基于变量协方差矩阵对数据进行压缩降维.去噪的有效方法,PCA的思想是将n维特征映射到k维上(k<n),这k维特征称为主元,是旧特征的线性组合,这些线性组合最大化样本方差 ...
随机推荐
- 【py技巧】使用reload重导入修改过的包或模块
#使用import导入 import my_module my_module.something() #out - orignal #这里修改输出 - changed reload(my_module ...
- Java Persistence API(转)
定义 Java Persistence API JPA通过JDK 5.0注解或XML描述对象-关系表的映射关系,并将运行期的实体对象持久化到数据库中.[编辑本段]起源 Sun引入新的JPA ORM规范 ...
- 随讲MyIsam和InnoDB的区别
mysiam表不支持事务处理,同时mysiam表不支持外键.外键不用说了吧?不知道的话,找度娘. 同时,在执行数据库写入的操作(insert,update,delete)的时候,mysiam表会锁表, ...
- DataSnap 的连接事件顺序图
无意看到这两幅图,虽然已经了解,还是转一份保留以备后用
- 关于全站https必要性http流量劫持、dns劫持等相关技术
关于全站https必要性http流量劫持.dns劫持等相关技术 微信已经要求微信支付,申请退款功能必须12月7号之前必须使用https证书了(其他目前为建议使用https),IOS也是2017年1月1 ...
- android listview万能适配器
参考 Android 快速开发系列 打造万能的ListView GridView 适配器 Hongyang public class CommonViewHolder { private Con ...
- LCD参数解释及计算【转】
转自:http://blog.csdn.net/longxiaowu/article/details/24319933 Linux内核的amba lcd控制器使用clcd_panel结构体表示一个LC ...
- git 本地分支与远程分支关联的一种方法
github上已经有master分支 和dev分支 在本地 git checkout -b dev 新建并切换到本地dev分支 git pull origin dev 本地分支与远程分支相关联 在本地 ...
- 约瑟夫问题 java
约瑟夫环:已知n个人(以编号1,2,3...n分别表示)围坐在一张圆桌周围.从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列;依此规律重复下去,直到圆桌周围 ...
- PMO终究什么样?(2)
PMO终究什么样?(2) 接上一篇,继续聊一聊PMO终究什么样. 交给功用,8大典型职责 1监控.鉴定和陈述 项目处理单位从交给的角度一定要有监控鉴定.每个项目在关键的时期上它的发展是不是跟如期的一样 ...
