hiho一下，第115周，FF,EK,DINIC

题目1 : 网络流一·Ford-Fulkerson算法

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

小Hi和小Ho住在P市，P市是一个很大很大的城市，所以也面临着一个大城市都会遇到的问题：交通拥挤。

小Ho：每到周末回家感觉堵车都是一种煎熬啊。

小Hi：平时交通也还好，只是一到上下班的高峰期就会比较拥挤。

小Ho：要是能够限制一下车的数量就好了，不知道有没有办法可以知道交通系统的最大承受车流量，这样就可以限制到一个可以一直很顺畅的数量了。

小Hi：理论上是有算法的啦。早在1955年，T.E.哈里斯就提出在一个给定的网络上寻求两点间最大运输量的问题。并且由此产生了一个新的图论模型：网络流。

小Ho：那具体是啥？

小Hi：用数学的语言描述就是给定一个有向图G=(V,E)，其中每一条边(u,v)均有一个非负数的容量值，记为c(u,v)≥0。同时在图中有两个特殊的顶点，源点S和汇点T。

举个例子：

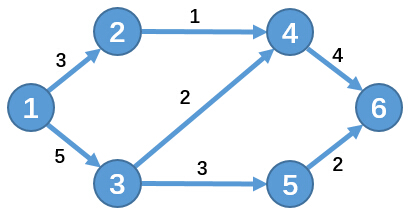
其中节点1为源点S，节点6为汇点T。

我们要求从源点S到汇点T的最大可行流量，这个问题也被称为最大流问题。

在这个例子中最大流量为5，分别为：1→2→4→6，流量为1；1→3→4→6，流量为2；1→3→5→6，流量为2。

小Ho：看上去好像挺有意思的，你让我先想想。

输入

第1行：2个正整数N,M。2≤N≤500，1≤M≤20,000。

第2..M+1行：每行3个整数u,v,c(u,v)，表示一条边(u,v)及其容量c(u,v)。1≤u,v≤N，0≤c(u,v)≤100。

给定的图中默认源点为1，汇点为N。可能有重复的边。

输出

第1行：1个整数，表示给定图G的最大流。

提示：Ford-Fulkerson算法

小Hi：在你思考完成之前，我再给你讲一些网络流的性质好了。

对于任意一个时刻，设f(u,v)实际流量，则整个图G的流网络满足3个性质：

1. 容量限制：对任意u,v∈V，f(u,v)≤c(u,v)。

2. 反对称性：对任意u,v∈V，f(u,v) = -f(v,u)。从u到v的流量一定是从v到u的流量的相反值。

3. 流守恒性：对任意u，若u不为S或T，一定有∑f(u,v)=0，(u,v)∈E。即u到相邻节点的流量之和为0，因为流入u的流量和u点流出的流量相等，u点本身不会"制造"和"消耗"流量。

对于上面例子中的图，其对应的f网络图为（其中虚线表示实际不存在的边(v,u)）：

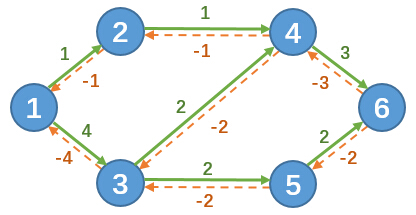
在此基础上，假设我们用cf(u,v)来表示c(u,v)-f(u,v)，则可以表示每一条边还剩下多少的流量可以使用，我们称为残留容量。

假设一条边(u,v)，其容量为3，使用了流量f(u,v)=2，则可以表示为：cf(u,v)=1, cf(v,u)=2。

由cf(u,v)构成的图我们称为残留网络。

比如例子中的残留网络图为：

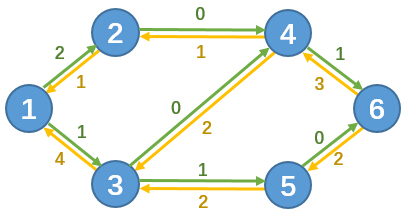
小Ho，你可以从残留网络作为着手点，会比较简单。

小Ho：残留网络，残留网络也就是可以使用的流量......我知道了！

既然残留网络表示还可以使用的流量，那么我就可以从图中找出一条从S到T的路径p，使得路径p上所有边的cf(u,v)都大于0。

假设路径p上最小的cf(u,v)等于k，那我就可以使得S到T增加k的流量。

小Hi：没错，通过该条路径p使得图G的最大流得到了增加，所以这样的路径p被称为增广路径。

小Ho：我大概有一个简单的算法了！

首先我根据读入的信息，就可以得到最初的图G，然后将其转化为残留网络。

接下来我在残留网络上寻找是否有增广路径，如果不存在增广路径，则说明这个图不能再增加流量了。

若存在增广路径，则我将最大流量增加，同时对增广路径上的边cf(u,v)进行修改，再重复寻找增广路径。

整个过程大概就是：

While ( findAugmentPath() ) // 判断是否有增广路
	maxFlow = maxFlow + delta // 最大流增加
	modifyGraph() // 对增广路进行修改
End While
		

小Hi：那么你打算怎么实现寻找增广路和修改路径呢？

小Ho：寻找增广路的话，直接使用BFS从源点S开始搜索，记录每个点的路径以及路径上的最小残余容量：

findAugmentPath():
queue = []    // 重置搜索队列
path = []     // 初始化路径数组为0
capacity = [] // 初始化流量数组为0
visited = []  // 初始化访问数组为false
tail = 0
queue[ tail ] = S // 将源点加入队列
capacity[S] = ∞ // 到源点的流量为无穷大
visited[S] = true
i = 0
While (i ≤ tail)
	u = queue[i]
	If (u == T) Then
		// 已经找到一条增广路
		Return capacity[T]
	End If
	For (u, v)∈残留网络 and cf(u,v)>0 and not visited[v]
		// u到v有残留容量，且v未被访问过
		path[v] = u // 记录路径
		capacity[v] = min(cf(u,v), capacity[u]) // 记录路径上的最小残余容量

		visited[v] = true
		tail = tail + 1
		queue[ tail ] = v
	End For
	i = i + 1
End While
		

而对于路径的修改，在已经有path数组的情况下，利用迭代或者回溯都可以完成：

modifyGraph():
flow = capacity[T]
now = T
While ( now is not S )
	fa = path[ now ]
	cf(fa, now) = cf(fa, now) - flow
	cf(now, fa) = cf(now, fa) + flow // 反向的残余容量是增加
	now = fa
End While
		

小Ho：时间复杂度方面，每一次寻找增广路的时间为O(n+m)，每一次修改路径的时间复杂度为O(n)。假设图的最大流为maxflow，那么我的算法时间复杂度为O((n+m)*maxflow)。

小Hi：嗯，你所采用的算法就是最简单的最大流解决办法，最早是由L.R.Ford和D.R.Fulkerson在1956年时发表，因此也被称为Ford-Fulkerson算法。对于第一次接触网络流而言，可以先试着实现这个算法，对于你理解网络流会有很大的帮助。

小Ho：不过小Hi，我有一个小疑问，虽然我直观上感觉找不到新的增广路时就已经是最大流了，但这真的没有问题么？

小Hi：找不到增广路确实是等价于找到最大流，不过具体的证明嘛，请听下回分解。

看了一下这个Ford-Fulkerson算法，感觉和EK很相似，都是BFS不断增广。

然后，我当时有个数组没有开足够，竟然是TLE，后来学了一下Dinic算法。

这里总结一下这3个算法：

Ford-Fulkerson: 也是最初的最大流算法，简单讲就是，不断DFS增广，直到找不到增广路。

Edmonds-Karp:是FF的变形，不断BFS增广，直到找不到增广路。

Dinic:BFS分层，DFS增广。

#include <bits/stdc++.h>

using namespace std;

#define maxn 505
#define INF 0x3f3f3f3f

struct Edge
{
    int from,to,cap,flow;
};

struct Dinic
{
    int n,m,s,t;
    vector<Edge> edge;
    vector<int> G[maxn];
    bool vis[maxn];
    int d[maxn];
    int cur[maxn];
    void addEdge (int from,int to,int cap)
    {
        edge.push_back((Edge){from,to,cap,});
        edge.push_back((Edge){to,from,,});
        m = edge.size();
        G[from].push_back(m-);
        G[to].push_back(m-);
    }

    bool BFS()
    {
        memset(vis,,sizeof(vis));
        queue<int> Q;
        Q.push(s);
        d[s] = ;
        vis[s] = ;
        while(!Q.empty())
        {
            int x = Q.front();
            Q.pop();
            for(int i=; i<G[x].size(); i++)
            {
                Edge & e = edge[G[x][i]];
                if(!vis[e.to]&&e.cap>e.flow)
                {
                    vis[e.to] = ;
                    d[e.to] = d[x] + ;
                    Q.push(e.to);
                }
            }
        }
        return vis[t];
    }

    int DFS(int x,int a)
    {
        if(x==t||a==) return a;
        int flow = ,f;
        for(int & i = cur[x]; i<G[x].size(); i++)
        {
            Edge & e = edge[G[x][i]];
            if(d[x] + ==d[e.to]&&(f=DFS(e.to,min(a,e.cap-e.flow)))>)
            {
                e.flow +=f;
                edge[G[x][i]^].flow -=f;
                flow +=f;
                a-=f;
                if(a==) break;
            }
        }
        return flow;
    }

    int Maxflow (int s,int t) {
        this->s = s;this->t = t;
        int flow = ;
        while(BFS()) {
            memset(cur,,sizeof(cur));
            flow+=DFS(s,INF);
        }
        return flow;
    }
}sol;

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=;i<m;i++) {
        int u,v,cap;
        scanf("%d%d%d",&u,&v,&cap);
        sol.addEdge(u,v,cap);
    }
    printf("%d\n",sol.Maxflow(,n));
    return ;
}