LG1268树的重量

#include<bits/stdc++.h>
using namespace std;
#define N 35
#define INF 1e9
int dis[N][N],n,len,ans;
int main(){
  while(scanf("%d",&n)){
    if(!n) break;
    for(int i=;i<=n;i++)
    for(int j=i+;j<=n;j++)
    scanf("%d",&dis[i][j]),dis[j][i]=dis[i][j];
    ans=dis[][];
    for(int i=;i<=n;i++){
        len=INF;
        for(int j=;j<=n;j++)
          for(int k=j+;k<=n;k++)
            if(j!=i && k!=i)
            len=min(len,(dis[i][j]+dis[i][k]-dis[j][k])/);
        ans+=len;
    }
    printf("%d\n",ans);
  }
    return ;
}

一道构造题。666

锻炼思维的好题，需要运用一些树的性质。以下用g(i,j)表示点i与点j之间的距离。

首先，我们考虑n=2时的情况，很显然答案就是g(1,2)。

接下来考虑n=3时的情况。由于所有点均为叶子节点，很显然点3是从点1到点2的路径上分叉出来的，就像下图。

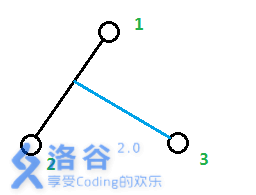
设蓝色部分长度为len，那么答案就是g(1,2)+len。len怎么求呢？显然，len = (g(1,3)+g(2,3)-g(1,2))/2。

n>3的情况也同理。枚举i，看看点n是不是从点1~i的路径上分叉出来的，求出的最小len就是要加到答案里面去的。如下图。

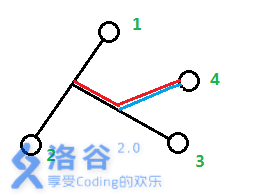
如果认为点4是从1~2的路径上分叉出来的，答案就会加上红色部分的长度。但是红色部分长度显然有一部分是多余的。只有认为点4是从1~3的路径上分叉出来的，才能加上正确答案（也就是蓝色部分）。