gym923B

Even though he isn't a student of computer science, Por Costel the pig has started to study Graph Theory. Today he's learning about Bellman-Ford, an algorithm that calculates the minimum cost path from a source node (for instance, node 1) to all the other nodes in a directed graph with weighted edges. Por Costel, utilizing his scarce programming knowledge has managed to scramble the following code in C++, a variation of the Bellman-Ford algorithm:

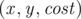You can notice a lot of deficiencies in the above code. In addition to its rudimentary documentation, we can see that Por Costel has stored this graph as an array of edges (the array ). An edge is stored as the triplet signifying an edge that spans from to 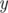and has weight 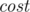. But even worse is the fact that the algorithm is SLOW!

As we want our hooved friend to walk away with a good impression about computer science, we want his code to execute as FAST as possible. In order to do so, we can modify the order of edges in the array so that the while loop executes a small number of times.

Given a directed graph of 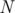nodes and edges, you are asked to produce an ordering of the edges such that the Bellman-Ford algorithm written by Por Costel should finish after at most two iterations of the while loop(that is, the program should enter the while loop at most twice).

Input

The first line of the file algoritm.in will contain an integer 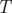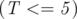, the number of test cases.

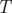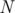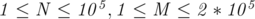Each of the test cases has the following format: on the first line, there are two numbers and (), the number of nodes and the number of edges in the graph respectively.

The next lines describe the edges, each containing three integers 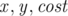signifying there is an edge from node to node 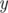with weight ()

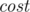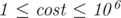It is guaranteed that node 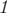has at least one outgoing edge.

The graph may contain self loops and/or multiple edges.

Output

The output file algoritm.out should contain 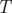lines representing the answers to each test case.

For each test case you should output a permutation of numbers from 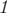to , representing the order of the edges you want in Por Costel's array of edges .

The edges are considered indexed by the order in which they are given in the input (the -th edge read is the edge with index ).

If there are multiple solutions, you are allowed to print any of them.

Example

Input

1
4 4
1 2 1
3 4 2
2 3 3
1 3 1

Output

1 4 2 3

dijiestra存访问路径

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
const int inf=1<<29;
typedef pair<int,int> PII;
struct edge
{
	int v,val,i;
};
priority_queue<PII,vector<PII>,greater<PII> >q;
vector<edge>graph[100100];
vector<int>num;
int n,m,u,v,val,T;
int d[100100],used[200100],use[200100];
void dijiestra()
{
	memset(used,0,sizeof(used));
	q.push(PII(0,1));
	while(!q.empty())
	{
		PII x=q.top();q.pop();
		int u=x.second;
		if(used[u]) continue;
		used[u]=1;
		for(int i=0;i<graph[u].size();i++)
		{
			edge x=graph[u][i];
			int v=x.v,val=x.val;
			if(d[v]>d[u]+val){d[v]=d[u]+val;num.push_back(x.i);use[x.i]=1;q.push(PII(d[v],v));}
		}
	}
//	for(int i=1;i<=n;i++) cout<<d[i]<<" ";
//	cout<<endl;
	for(int i=0;i<num.size();i++) printf("%d ",num[i]);
	for(int i=1;i<=m;i++) if(!use[i]) printf("%d ",i);
	cout<<endl;
}
int main()
{
	freopen("algoritm.in","r",stdin);
	freopen("algoritm.out","w",stdout);
	cin>>T;
	while(T--)
	{
		cin>>n>>m;
		for(int i=2;i<=n;i++) d[i]=inf;
		memset(use,0,sizeof(use));
		num.clear();
		for(int i=1;i<=m;i++)
		{
			scanf("%d%d%d",&u,&v,&val);
			edge e;
			e.v=v,e.val=val,e.i=i;
			graph[u].push_back(e);
		}
		dijiestra();
		for(int i=1;i<=n;i++)
			graph[i].clear();
	}
	fclose(stdin);
	fclose(stdout);
	return 0;
}