机器学习-线性分类-支持向量机SVM-SMO算法-14

目录

• 1. SVM算法总结
• 2. SMO算法

1. SVM算法总结

1. 选择 核函数 以及对应的 超参数
   
   为什么要选择核函数？
   
   升维 将线性问题不可分问题 升维后转化成 线性可分的问题
   
   核函数 有那些？ linea gauss polinormail tanh

2. 选择惩罚项系数C
   
   min ||w||2 + Csum(ei)

3. 构造优化问题：
   
   

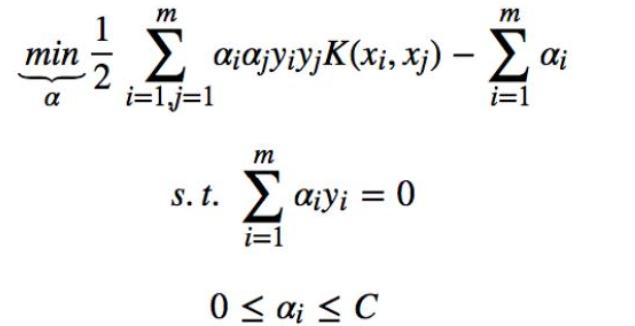
4. 利用SMO算法 计算 α*

5. 根据α* 计算w*

6. 根据α* 得到支撑向量 计算每个支撑向量 对应的bs*

7. bs* 求平均得到b*
   
   学得超平面：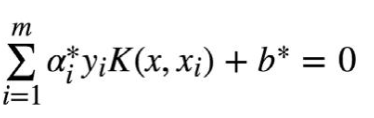
   
   仔细观察这个式子就会发现：
   
   其实只需要关注 支撑向量的C>α>0 非支撑向量的alpha为0
   
   W*的计算：
   
   

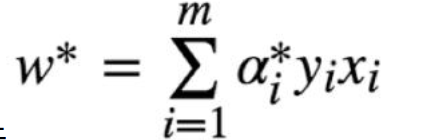
其实也就只需要关注 是支撑向量的几个点，支撑向量对于W,b的求解起关键作用，其他的非支撑向量，对模型没起任何作用

1. 得到最终的判别式
   
   

神奇的SMO算法到底是如何进行的？

2. SMO算法

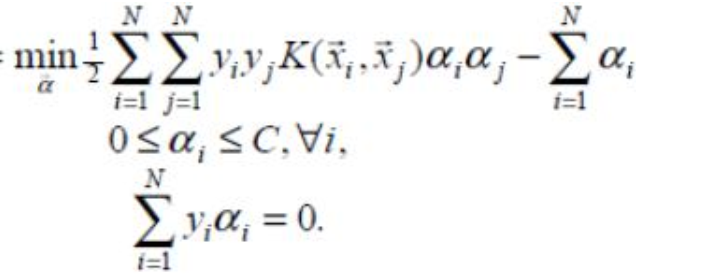
其中(xi,yi)表示训练样本数据，xi 为样本特征，yi∈{−1,1}为样本标签，C 为惩罚系数由自己设定。上述问题是要求解 N 个参数(α1,α2,α3,...,αN)，其他参数均为已知

把原始求解 N 个参数二次规划问题分解成很多个子二次规划问题分别求解，每个子问题只需要求解 2 个参数，方法类似于坐标上升，节省时间成本和降低了内存需求。每次启发式选择两个变量进行优化，不断循环，直到达到函数最优值。

同时优化两个参数，固定其他 N-2 个参数，假设选择的变量为α1,α2,

固定其他参数α3,α4,...,αN,由于参数α3,α4,...,αN 的固定， 可以简化目标函数为只关于α1,α2的二元函数，Constant 表示常数项(不包含变量α1,α2 的项)。

v1 表示 x1 与 3---N 之后所有的样本运算

v2 表示 x2 与 3---N 之后所有的样本运算

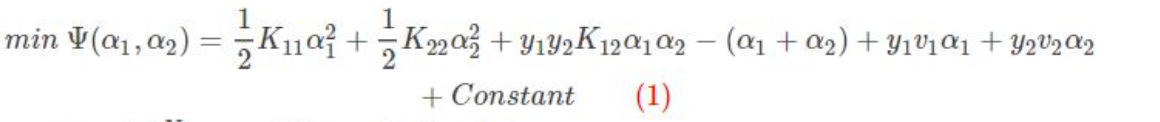
其中：

Kij表示 xi 与 xj 输入到核函数 进行运算的结果



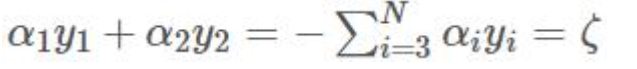
两边同时乘以 y1， 任意的y*2 = 1

得到：

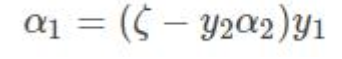
需要优化的目标函数转化成：

上式中是关于变量α2 的函数，对上式求导并令其为 0 得：

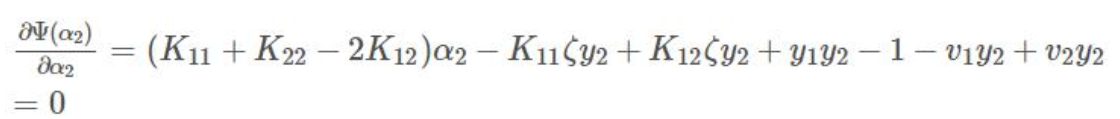
将4， 6， 7 带入求导=0 的式子



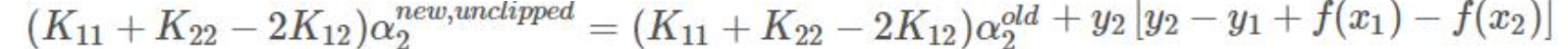
令η=K11+K22−2K12



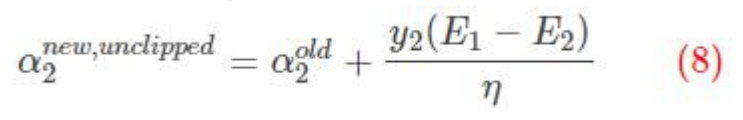
这里得到的α2 是未经过修建的alpha 不一定满足约束条件

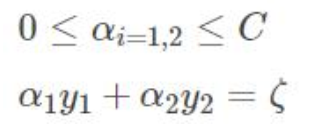
翻译一下：

两个拉格朗日算子 0< α1 α2 < C限定必须在正方形盒子内部

α1y1+α2y2=固定值 限定了必须在直线上 最优解 必须是一条线段

新的α2 下限L 上限H

修建后的alpha



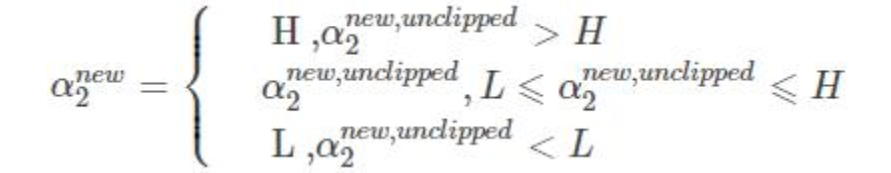
由于其他 N-2 个变量固定：

两边同时乘以y1：

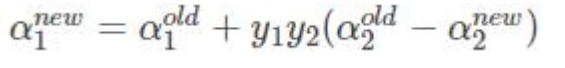
选择α1 α2采用上述方法进行优化，直到不违反kkt条件

α1 α2优化的同时对b进行更新：

1. 如果：
   
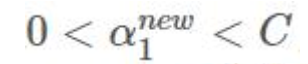
   则 x1 y1 为支撑向量
   
   两边乘以y1：
   
   

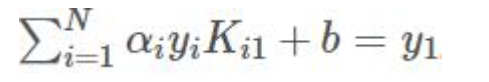
得到bnew：



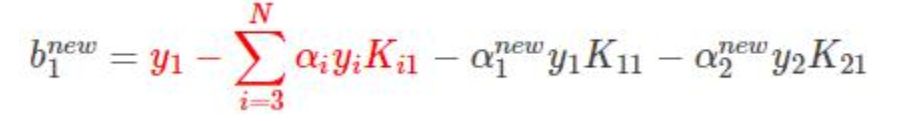
只不过是拆成3部分而已

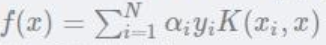
前两项可以替换为



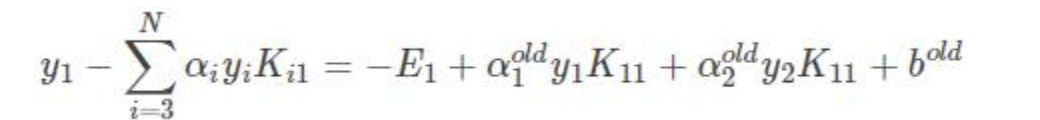
得到：

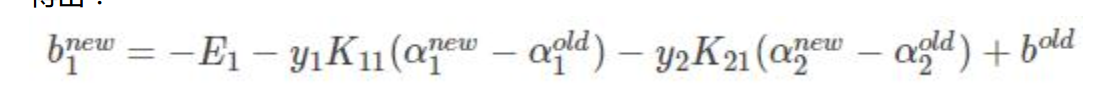
如果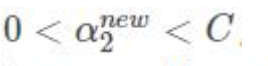

同理：

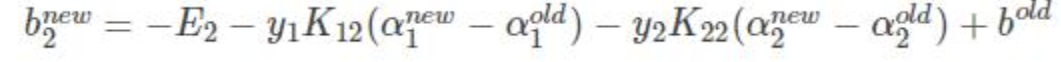
1. α1 α2 都满足：
   
   
   
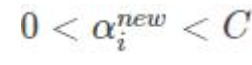
   取一个就行：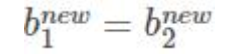

2. 如果都不满足 他们的中点：
   
   取1/2 *（α1 + α2）