快速傅里叶变换（FFT）和小波分析在信号处理上的应用

1前言

1.1傅里叶变换

函数f(t)为一元连续函数，其傅里叶变换定义为：



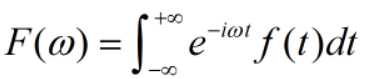
F(w)的傅里叶逆变换定义为：



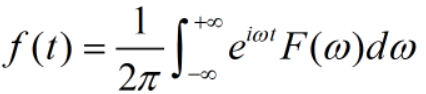
其中，i为虚数单位。由欧拉公式：



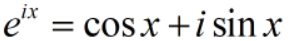
任意绝对可积的连续函数f(t)，都可以用三角函数表示，由于三角函数是周期函数，由此可展开为傅里叶级数。本文不加证明地给出傅里叶级数展开式：



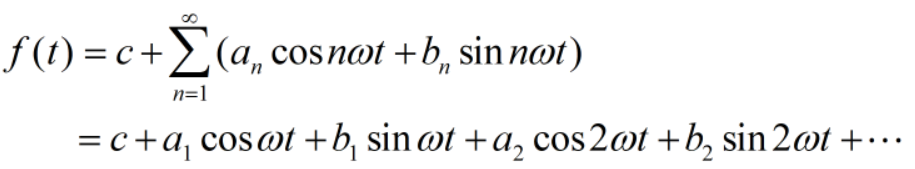
设F是所有由一元连续的绝对可积的函数组成的空间，由傅里叶级数知



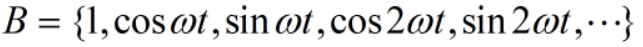
是F的一组基，即对任意的f(t)属于F，都可以用这组基表示。

实际上，cos(0wt)=1，sin(0wt)=0，但是由于0乘任何数都等于0，不能作为基。这就将基都是由三角函数组成统一起来了。

对任意f(t)、g(t)属于F，定义内积如下：



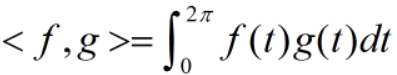
由此，对任意f(t)、g(t)属于B，有



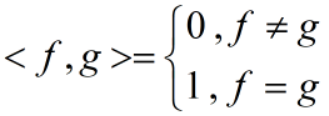
所以，B是F的一组标准正交基。对任意f(t)属于F，由内积导出范数：



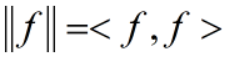
在《泛函分析》中，已证明F为完备的赋范线性空间，进一步可得，F为希尔伯特（Hibert）空间。

那么，如何求一个函数f(t)的傅里叶展开式？这时，傅里叶变换就派上用场了。

设f(t)的傅里叶展开式如下：



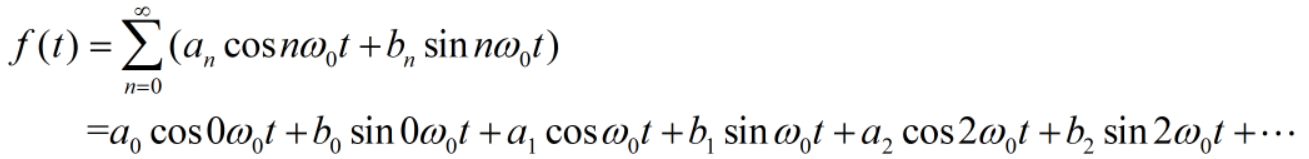
假设已经求得f(t)的傅里叶变换函数F(w)，如何利用F(w)求得a_m，b_m（m=0,1,2,...）？

实际上a_m，b_m分别是F(mw_0t)的实部(a)和虚部的相反数(-b)，即：



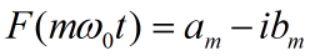
证明如下：



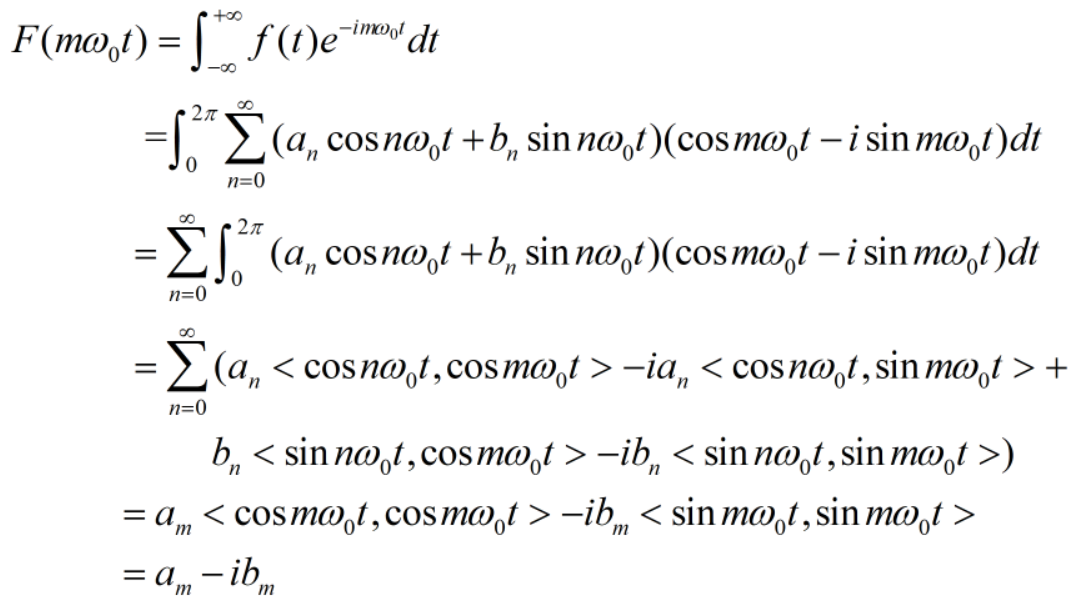
其实，傅里叶变换的作用不仅限于此，在求解微分方程时，能够将复杂的积分运算转换成简单的线性运算。对微分方程两边同时进行傅里叶变换，原微分方程就转化为普通一元方程，求出一元方程的解后，再进行傅里叶逆变换，就得到原微分方程的解。读者若对傅里叶级数很感兴趣，请参见《复变函数》。

在信号处理中，傅里叶级数又扮演着什么样的角色？在工程应用中，信号函数f(t)一般极其复杂，往往还夹杂着噪声，无法通过函数图像看出其包含的基本波形频率及振幅。设信号f(t)的傅里叶展开式为：



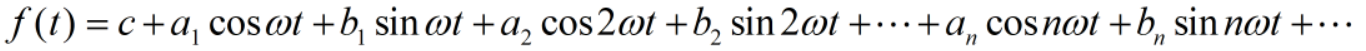
通过辅助角公式：



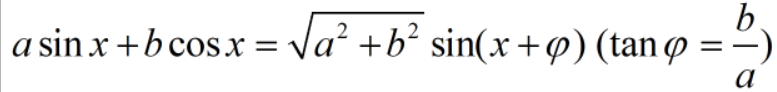
f(t)可以转化为如下形式：



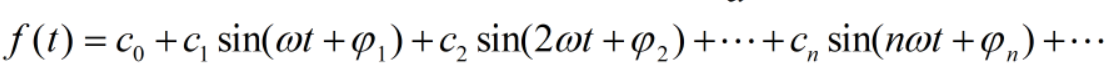
可以看出频率和振幅信息。其中nw为频率，c_n为振幅，反映了波的能量大小。当c_n比较小时，说明该频率的波能量较小，可认为是噪声波，去掉该项，再将留下来的波进行重构，起到去噪作用。如果以nw为横坐标，c_n为纵坐标，信号f(t)的信息又可用一串（nw,c_n）点表示，由此得到频谱图。即将时域信息转换为频域信息。

1.2小波分析

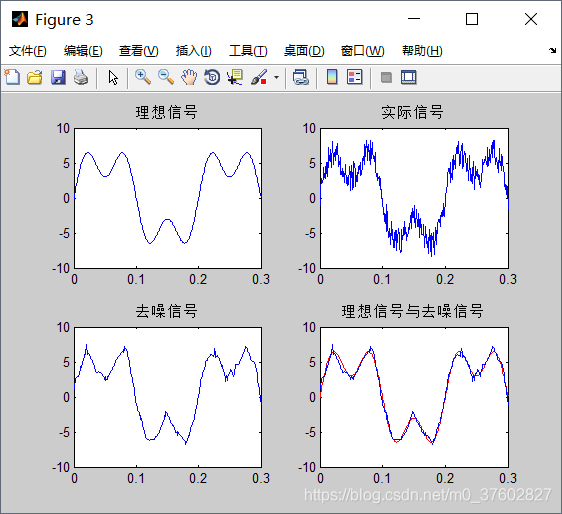
小波分析在FFT的基础上，将波形进行改进。FFT以正玄波为母波（余弦波可通过正弦波移相得到），通过增大频率得到一列子波，来建立一组基。小波分析采用更加灵活的波形。如下图，如果1号波的频率为1，那么2号和3号波的频率分别为2、4。



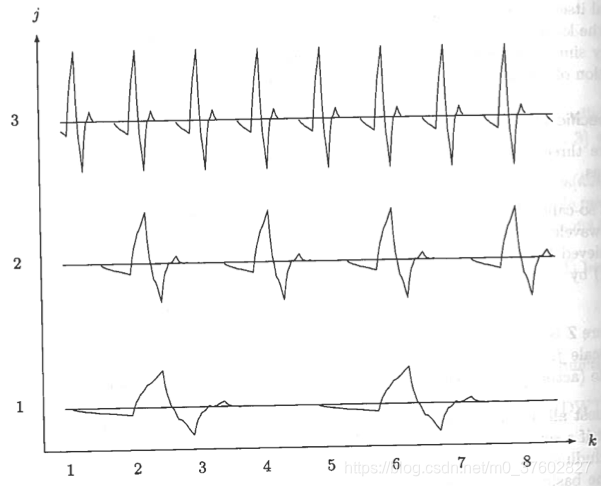
常用的小波如下：

（1）RbioNr.Nd小波（reverse双正交小波）

（2）Gaus小波（由高斯函数派生出）

（3）Dmey小波（Meyer函数的近似，能快速进行小波变换）

（4）Cgau小波（复数形式的高斯小波）

（5）Cmor小波（复数形式的morlet小波）

（6）Fbsp小波（复频域B样条小波）

2信号信息

本文以频率和振幅分别f1=5Hz、a1=6，f2=15Hz、a2=3的两列波为理想信号，以0均值、振幅不超过4的随机扰乱信号为噪声波，两者叠加得到实际波。代码如下：

clear,clc
N=300; %信号采样个数（300个）
F=1000; %采样频率（1000Hz）
t=linspace(0,0.3,N); %时间向量,0.3s采样300个样本，采样频率为1000Hz
%%%%%%%%%%%%%%%%%%%%1.波信号信息%%%%%%%%%%%%%%%%%%%%
x=6*sin(2*pi*5*t)+3*sin(2*pi*15*t); %理想信号（f1=5Hz，a1=6；f2=15Hz，a2=3）
y=4*(rand(1,N)-0.5); %噪声信号（0均值随机扰动）
z=x+y; %实际信号
figure
subplot(221)
plot(t,x);
xlim([0 0.3])
title('理想信号');
subplot(222)
plot(t,y);
xlim([0 0.3])
title('噪声信号');
subplot(223)
plot(t,z);
xlim([0 0.3])
title('实际信号');
subplot(224)
plot(t,x,'linewidth',3.0); %加粗曲线
xlim([0 0.3])
hold on
plot(t,z,'--r')
title('理想信号与实际信号');

运行结果：

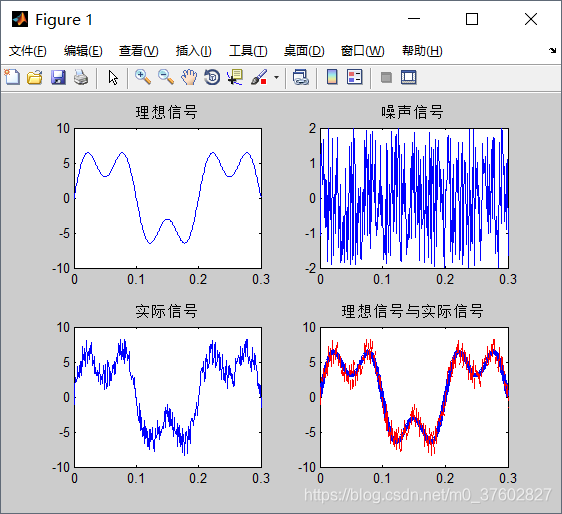
3应用快速傅里叶变换（FFT）获取信号频谱图

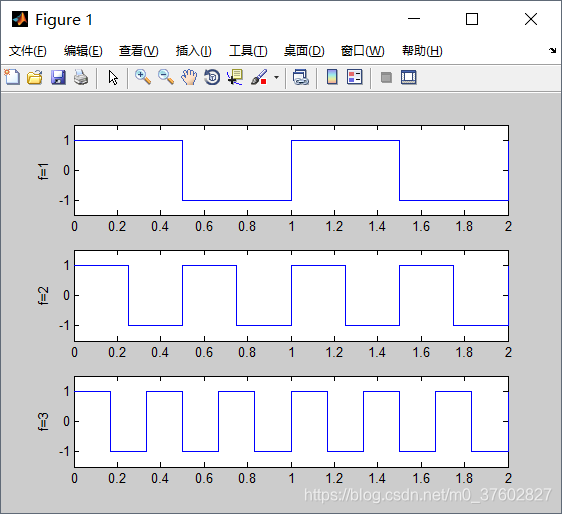
频谱图，即振幅与频率的关系图。由傅里叶展开式：



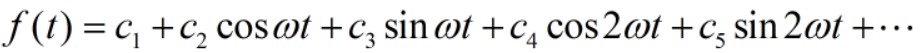
傅里叶展开式每一项前面的系数ci为频谱图的纵轴，每一项内部的系数wn为横轴。代码如下：

%%%%%%%%%%%%%%%%%%%%2.应用FFT（快速傅里叶变换）获取信号频谱图%%%%%%%%%%%%%%%%%%%%
n=2^nextpow2(N); %参加FFT的采样点个数为512（300后面的2的指数函数值）
fly=fft(z,n); %对原始信号进行离散傅里叶变换
a=abs(2*fly/N); %振幅
f=F/2*linspace(0,1,n/2+1); %频率
figure
plot(f(1:80),a(1:80)); %绘制信号频谱图
title('频谱图');
xlabel('频率');
ylabel('振幅');

运行结果：



曲线和横轴围成的面积反应了波的能量。从上图可以看出，振幅和频率分别为f1=5Hz、a1=6，f2=15Hz、a2=3的两列波附近的能量比较高，可认为是有效信号，而其他波形附近的能量都比较弱，可认为是噪声。

4应用小波分析进行去噪处理

删除信号f(t)傅里叶展开式中振幅ci较小的波，将留下来的波进行波形重构，就达到去噪目的。代码如下：

%%%%%%%%%%%%%%%%%%%%3.应用小波分析进行去噪处理%%%%%%%%%%%%%%%%%%%%
xb=wden(z,'minimaxi','s','one',4,'db3');
figure
subplot(221)
plot(t,x);
xlim([0 0.3])
title('理想信号');
subplot(222)
plot(t,z);
xlim([0 0.3])
title('实际信号');
subplot(223)
plot(t,xb);
xlim([0 0.3])
title('去噪信号');
subplot(224)
plot(t,x,'r',t,xb);
xlim([0 0.3])
title('理想信号与去噪信号');

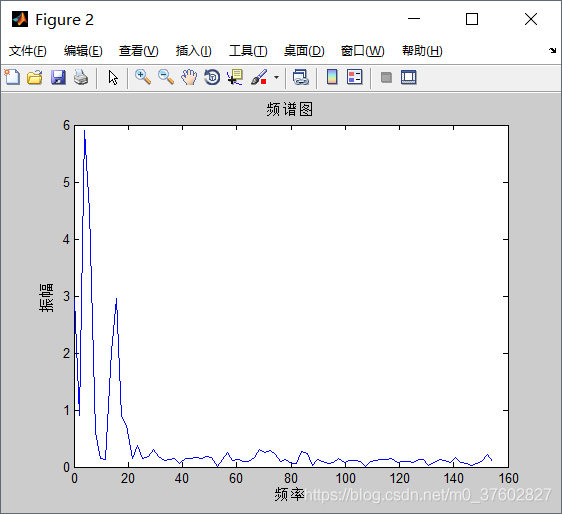
运行结果：

5应用小波分析进行信号压缩

曲线的信息量远比直线的信息量高，若以硬极核函数为小波，就可对原信号进行压缩。



代码如下：

%%%%%%%%%%%%%%%%%%%%4.应用小波分析进行信号压缩%%%%%%%%%%%%%%%%%%%%
figure
subplot(321);
plot(t,z);
xlim([0 0.3])
title('实际信号');
alpha=1.4;
for i=1:5
    [C,L]=wavedec(x,i,'haar'); %使用haar小波对信号进行i层分解
    thr=wdcbm(C,L,alpha); %获取信号压缩的阈值（threshold）
    xd=wdencmp('lvd',C,L,'haar',i,thr,'s'); %对信号进行压缩
    subplot(3,2,i+1);
    plot(t,xd);
    xlim([0 0.3])
    ylabel([num2str(i),'层分解']);
end

运行结果：



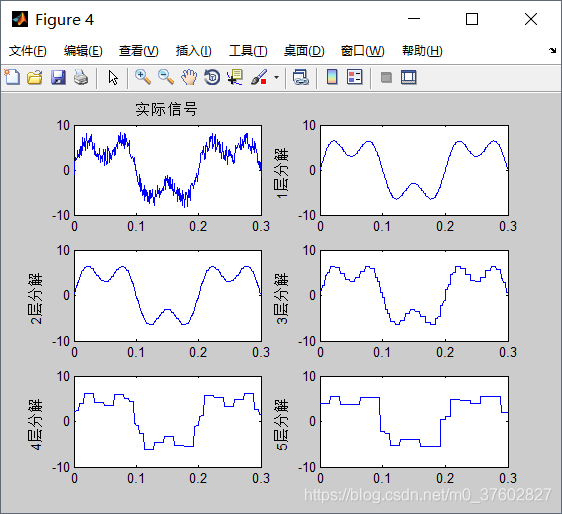
可以看到，压缩后的信号中有明显的线段。好比同一张照片，若降低像素，可以看到明显的格点。

6应用小波分析进行信号分离

代码如下：

%%%%%%%%%%%%%%%%%%%%5.应用小波分析进行信号分离%%%%%%%%%%%%%%%%%%%%
[C,L]=wavedec(z,5,'db5'); %使用db5小波对信号进行5层分解
figure;
subplot(321);
plot(t,z);
xlim([0 0.3])
ylabel('实际信号');
for i=1:5
    %对分解的第5层到第1层的低频系数进行重构
    A=wrcoef('A',C,L,'db5',6-i);
    subplot(3,2,i+1);
    plot(t,A);
    xlim([0 0.3])
    ylabel(['A',num2str(6-i)]);
end
figure;
subplot(321);
plot(t,z);
xlim([0 0.3])
ylabel('实际信号');
for i=1:5
    % 对分解的第5层到第1层的高频系数进行重构
    D=wrcoef('D',C,L,'db5',6-i);
    subplot(3,2,i+1);
    plot(t,D);
    xlim([0 0.3])
    ylabel(['D',num2str(6-i)]);
end

运行结果：

（1）对分解的第5层到第1层的低频系数进行重构



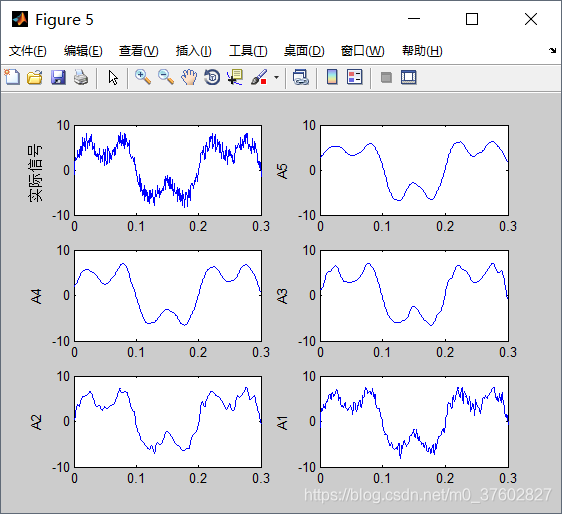
本例的理想信号的两列波的频率分别为f1=5Hz、f2=15Hz，都属于低频波，所以重构效果较好。

（2）对分解的第5层到第1层的高频系数进行重构



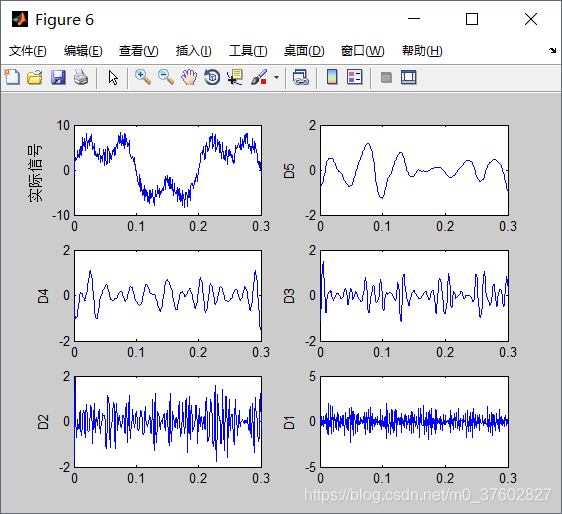
本例的理想信号的两列波的频率都属于低频波，而高频波主要是噪音，所以重构效果较差。

7全部代码

clear,clc
N=300; %信号采样个数（300个）
F=1000; %采样频率（1000Hz）
t=linspace(0,0.3,N); %时间向量,0.3s采样300个样本，采样频率为1000Hz
%%%%%%%%%%%%%%%%%%%%1.波信号信息%%%%%%%%%%%%%%%%%%%%
x=6*sin(2*pi*5*t)+3*sin(2*pi*15*t); %理想信号（f1=5Hz，a1=6；f2=15Hz，a2=3）
y=4*(rand(1,N)-0.5); %噪声信号（0均值随机扰动）
z=x+y; %实际信号
figure
subplot(221)
plot(t,x);
xlim([0 0.3])
title('理想信号');
subplot(222)
plot(t,y);
xlim([0 0.3])
title('噪声信号');
subplot(223)
plot(t,z);
xlim([0 0.3])
title('实际信号');
subplot(224)
plot(t,x,'linewidth',3.0); %加粗曲线
xlim([0 0.3])
hold on
plot(t,z,'--r')
title('理想信号与实际信号');
%%%%%%%%%%%%%%%%%%%%2.应用FFT（快速傅里叶变换）获取信号频谱图%%%%%%%%%%%%%%%%%%%%
n=2^nextpow2(N); %参加FFT的采样点个数为512（300后面的2的指数函数值）
fly=fft(z,n); %对原始信号进行离散傅里叶变换
a=abs(2*fly/N); %振幅
f=F/2*linspace(0,1,n/2+1); %频率
figure
plot(f(1:80),a(1:80)); %绘制信号频谱图
title('频谱图');
xlabel('频率');
ylabel('振幅');
%%%%%%%%%%%%%%%%%%%%3.应用小波分析进行去噪处理%%%%%%%%%%%%%%%%%%%%
xb=wden(z,'minimaxi','s','one',4,'db3');
figure
subplot(221)
plot(t,x);
xlim([0 0.3])
title('理想信号');
subplot(222)
plot(t,z);
xlim([0 0.3])
title('实际信号');
subplot(223)
plot(t,xb);
xlim([0 0.3])
title('去噪信号');
subplot(224)
plot(t,x,'r',t,xb);
xlim([0 0.3])
title('理想信号与去噪信号');
%%%%%%%%%%%%%%%%%%%%4.应用小波分析进行信号压缩%%%%%%%%%%%%%%%%%%%%
figure
subplot(321);
plot(t,z);
xlim([0 0.3])
title('实际信号');
alpha=1.4;
for i=1:5
    [C,L]=wavedec(x,i,'haar'); %使用haar小波对信号进行i层分解
    thr=wdcbm(C,L,alpha); %获取信号压缩的阈值（threshold）
    xd=wdencmp('lvd',C,L,'haar',i,thr,'s'); %对信号进行压缩
    subplot(3,2,i+1);
    plot(t,xd);
    xlim([0 0.3])
    ylabel([num2str(i),'层分解']);
end
%%%%%%%%%%%%%%%%%%%%5.应用小波分析进行信号分离%%%%%%%%%%%%%%%%%%%%
[C,L]=wavedec(z,5,'db5'); %使用db5小波对信号进行5层分解
figure;
subplot(321);
plot(t,z);
xlim([0 0.3])
ylabel('实际信号');
for i=1:5
    %对分解的第5层到第1层的低频系数进行重构
    A=wrcoef('A',C,L,'db5',6-i);
    subplot(3,2,i+1);
    plot(t,A);
    xlim([0 0.3])
    ylabel(['A',num2str(6-i)]);
end
figure;
subplot(321);
plot(t,z);
xlim([0 0.3])
ylabel('实际信号');
for i=1:5
    % 对分解的第5层到第1层的高频系数进行重构
    D=wrcoef('D',C,L,'db5',6-i);
    subplot(3,2,i+1);
    plot(t,D);
    xlim([0 0.3])
    ylabel(['D',num2str(6-i)]);
end

8参考链接

[1] 傅里叶分析之掐死教程（完整版）

声明：本文转自快速傅里叶变换（FFT）和小波分析在信号处理上的应用