R_回归模型实例一

工作和生活中存在大量的具有相关性的事件，当找到不同变量之间的关系，我们就会用到回归分析。回归分析（Regression Analysis)：是用来确定2个或2个以上变量间关系的一种统计分析方法。

在回归分析中，变量有2类：因变量 和 自变量。

• 因变量：通常是指实际问题中所关心的指标，用Y表示。
• 自变量：是影响因变量取值的一个变量，用X表示，如果有多个自变量则表示为X1, X2, …, Xn。

回归分析研究的主要步骤：

1. 确定因变量Y 与 自变量X1, X2, …, Xn 之间的定量关系表达式，即回归方程。
2. 对回归方程的置信度检查。
3. 判断自变量Xn(n=1,2,…,m)对因变量的影响。
4. 利用回归方程进行预测。

假设X和Y的关系是线性，可以用公式表式为：Y = a + b * X + c

• Y，为因变量
• X，为自变量
• a，为截距（Intercept）
• b，为自变量系数
• a+b*X, 表示Y随X的变化而线性变化的部分
• c, 为残差或随机误差，是其他一切不确定因素影响的总和，其值不可观测。假定c是符合均值为0方差为σ^2的正态分布 ，记作c~N(0,σ^2)

对于上面的公式，称函数f(X) = a + b * X 为一元线性回归函数，a为回归常数，b为回归系数，统称回归参数。X 为回归自变量或回归因子，Y 为回归因变量或响应变量。

实例 

---

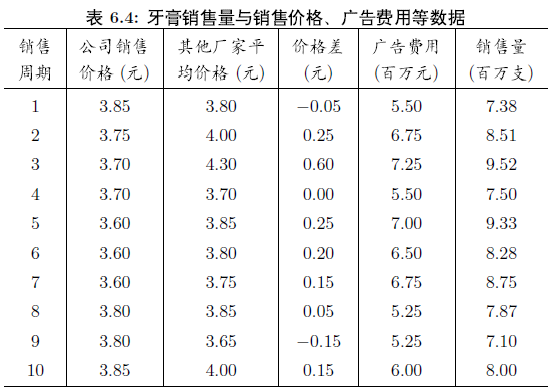
牙膏销售的实例：数据结构及示例化如下

• 

分析： 对于大多数顾客来说，在购买同类牙膏时，更多的会关心不同品牌之间的价格差，而不是它们的价格本身。因此，在研究各个因素对销售量的影响时，用价格差代替公司销售价格和其他厂家平均价格更为合适。

在计算过程中并不一定要知道Y和X是否有线性相关的关系。如果不存相关关系，那么回归方程就没有任何意义了，如果Y和X是有相关关系的，即Y会随着X的变化而线性变化。所以，我们需要用假设检验的方法，来验证相关性的有效性。

通常会采用三种显著性检验的方法：

• T检验法：T检验是检验模型某个自变量Xi对于Y的显著性，通常用P-value判断显著性，小于0.01更小时说明这个自变量Xi与Y相关关系显著。
• F检验法：F检验用于对所有的自变量X在整体上看对于Y的线性显著性，也是用P-value判断显著性，小于0.01更小时说明整体上自变量与Y相关关系显著。
• R^2(R平方)相关系统检验法：用来判断回归方程的拟合程度，R^2的取值在0，1之间，越接近1说明拟合程度越好。

回归模型拟合数据

---

当两个变量之间存在非常强烈的相互依赖关系的时候，我们就可以说两个变量之间的存在高度相关性。若两组的值一起增大，我们称之为正相关，若一组的值增大时，另一组的值减小，我们称之为负相关。

在使用回归模型拟合数据之前，我们先来观察自变量与因变量之间是如何相关的，我们求出除周期这一列外，其它各列的相关系数矩阵

观察发现sales销售量列的相关系数绝对值越大，相关性越强。注：R中cor函数来计算相关性也是有局限的，它不能计算非线性模型。

 基本模型

---

利用散点图观察销售量与价格差和广告费用的关系

library(ggplot2)
mytable <- read.csv("price.csv")
gplot(mytable,aes(x=mytable$DifPrice,y=mytable$sales))+geom_point()+labs(x="价格差",y="销售量")+geom_smooth(se=F)+theme_bw()
ggplot(mytable,aes(x=mytable$price,y=mytable$sales))+geom_point()+labs(x="价格",y="销售量")+geom_smooth(se=F)+theme_bw()
ggplot(mytable,aes(x=mytable$Invest,y=mytable$sales))+geom_point()+labs(x="广告费",y="销售量")+geom_smooth(se=F)+theme_bw()

    

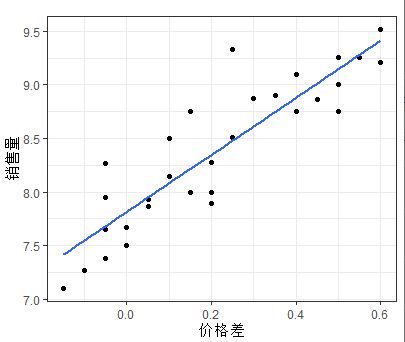
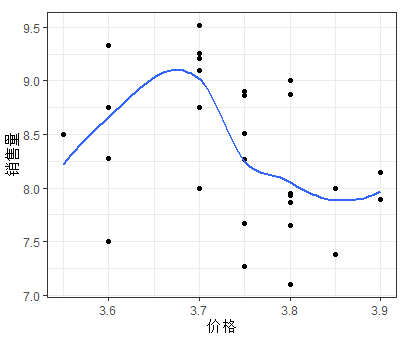
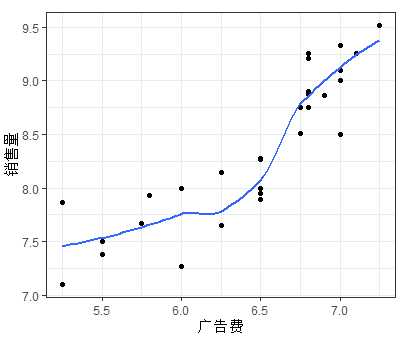
如上图可以发现随着价格差（x1）的增加，销售量（y）有比较明显的线型增长趋势；随着广告费用的增加，销售量有向上弯曲增加的趋势；

 模型求解

---

• Residuals（残差）：列出了残差的最小值点，1/4分位点，中位数点，3/4分位点，最大值点。
• Coefficients（系数）：表示参数估计的计算结果。Residual standard error：表示残差的标准差，自由度为n-2
  • Estimate（估计）：参数估计列。Intercept行表示常数参数a的估计值
  • Std. Error：为参数的标准差，sd(a), sd(b)
  • t value：为t值，为T检验的值
  • Pr(>|t|) ：表示P-value值，用于T检验判定，匹配显著性标记
  • 显著性标记：***为非常显著，**为高度显著, **为显著，·为不太显著，没有记号为不显著。
• Multiple R-squared：为相关系数R^2的检验，越接近1则越显著。
• Adjusted R-squared：为相关系数的修正系数，解决多元回归自变量越多，判定系数R^2越大的问题。
• F-statistic：表示F统计量，自由度为(1,n-2)
• p-value：用于F检验判定，匹配显著性标记。

模型改进

---

从如上的散点图可以看出，随着广告投入增加，销售量有向上弯曲增加的趋势。这里我们将广告投入的自变量换为二阶项来。则将销售量模型改为：

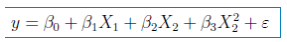
用lm函数拟合以上模型特征：

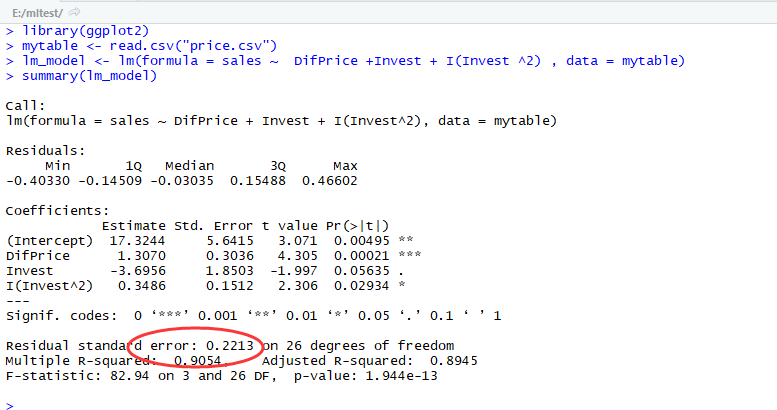
此时，我们发现，模型残差的标准差Residual standard error有所下降，相关系数的平方Multiple R-squared有所上升，这说明模型修正的是合理的。但同时也出现了一个问题，就是对于β2的P-值>0.05。

在做进一步的修正，考虑X1和X2交互作用，及模型为：

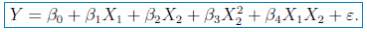
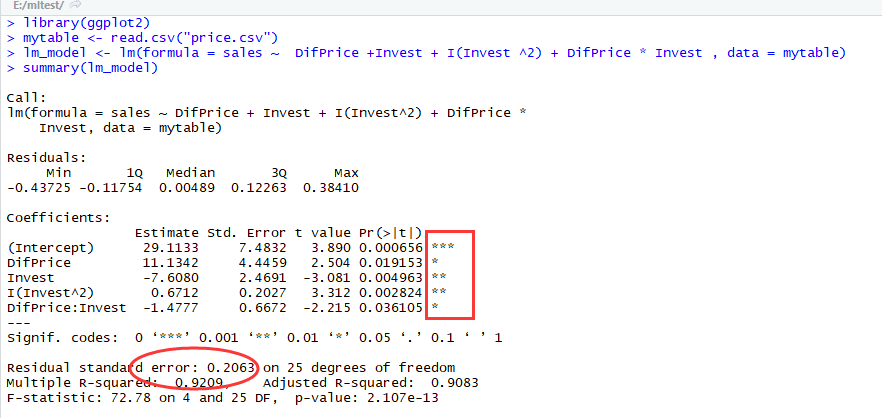
模型通过T检验和F检验，并且Residual standard error减少，Multiple R-squared增加。因此，最终模型选为：

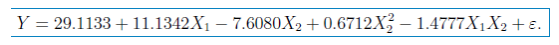
标准化

---

 

参考

---

• https://www.cnblogs.com/nxld/p/6138781.html
• https://blog.csdn.net/yitian_z/article/details/103097349
• https://www.jianshu.com/p/ec3d16ff7b45
• https://zhuanlan.zhihu.com/p/35850444