优化算法之梯度下降｜Matlab实现梯度下降算法

题目要求：

使用Matab实现梯度下降法

对于函数：

min

⁡

f

(

x

)

=

2

x

1

2

+

4

x

2

2

−

6

x

1

−

2

x

1

x

2

\min f(x)=2 x_{1}^{2}+4 x_{2}^{2}-6 x_{1}-2 x_{1} x_{2}

minf(x)=2x12​+4x22​−6x1​−2x1​x2​
试采用 MATLAB实现最速下降法求解该问题, 给出具体的迭代过程、 最终优化结果、涉及的代码, 以及自己的心得体会。

摘要

文章主要通过实现grad()函数进行梯度运算。

主要实现的功能：

1. 通过Matlab语言实现梯度下降算法
2. 利用Matlab的plot3描绘出梯度下降循环迭代的过程，同时也描绘出极小值随迭代次数的图像。

梯度下降原理

梯度的概念

梯度：是一个向量，表示某一函数在该点处的方向导数沿着该方向取得最大值。

• 有大小：变化率最大（为该梯度的模）；

• 有方向：函数在该点处沿着该方向（此梯度的方向）变化最快

定义：
设

z

=

f

(

x

,

y

)

z=f(x,y)

z=f(x,y)在点

P

0

(

x

0

,

y

0

)

P_{0}\left(x_{0}, y_{0}\right)

P0​(x0​,y0​)处存在偏导数

f

x

′

(

x

0

,

y

0

)

f_{x}^{\prime}\left(x_{0}, y_{0}\right)

fx′​(x0​,y0​)和

f

y

′

(

x

0

,

y

0

)

f_{y}^{\prime}\left(x_{0}, y_{0}\right)

fy′​(x0​,y0​),则称向量

{

f

x

′

(

x

0

,

y

0

)

,

f

y

′

(

x

0

,

y

0

)

}

\left\{f_{x}^{\prime}\left(x_{0}, y_{0}\right), f_{y}^{\prime}\left(x_{0}, y_{0}\right)\right\}

{fx′​(x0​,y0​),fy′​(x0​,y0​)}为

f

(

x

,

y

)

在

P

0

(

x

0

,

y

0

)

f(x, y) \text { 在 } P_{0}\left(x_{0}, y_{0}\right)

f(x,y) 在 P0​(x0​,y0​)的梯度，记作：

∇

f

∣

P

0

,

∇

z

∣

P

0

,

gradf

⁡

∣

P

0

或

gradz

⁡

∣

P

0

\left.\nabla f\right|_{P_{0}},\left.\nabla z\right|_{P_{0}},\left.\operatorname{gradf}\right|_{P_{0}} 或 \left.\operatorname{gradz}\right|_{P_{0}}

∇f∣P0​​,∇z∣P0​​,gradf∣P0​​或gradz∣P0​​

∴

∇

f

∣

P

0

=

gradf

⁡

∣

P

0

=

{

f

x

′

(

x

0

,

y

0

)

,

f

y

′

(

x

0

,

y

0

)

}

\left.\therefore \nabla f\right|_{P_{0}}=\left.\operatorname{gradf}\right|_{P_{0}}=\left\{f_{x}^{\prime}\left(x_{0}, y_{0}\right), f_{y}^{\prime}\left(x_{0}, y_{0}\right)\right\}

∴∇f∣P0​​=gradf∣P0​​={fx′​(x0​,y0​),fy′​(x0​,y0​)}
其中：

∇

\nabla

∇(Nabla)算子:

∇

=

∂

∂

x

i

+

∂

∂

y

j

\nabla=\frac{\partial}{\partial x} i+\frac{\partial}{\partial y} j

∇=∂x∂​i+∂y∂​j

梯度函数：

梯度的大小：

∣

∇

f

∣

=

[

f

x

′

(

x

,

y

)

]

2

+

[

f

y

′

(

x

,

y

)

]

2

|\nabla f|=\sqrt{\left[f_{x}^{\prime}(x, y)\right]^{2}+\left[f_{y}^{\prime}(x, y)\right]^{2}}

∣∇f∣=[fx′​(x,y)]2+[fy′​(x,y)]2

​

梯度的方向：

设：

v

=

{

v

1

,

v

2

}

(

∣

v

∣

=

1

)

v=\left\{v_{1}, v_{2}\right\}(|v|=1)

v={v1​,v2​}(∣v∣=1)是任一给定方向，则对

∇

f

\nabla f

∇f与

v

v

v的夹角

θ

\theta

θ有：

∂

f

∂

v

∣

P

0

=

f

x

′

(

x

0

,

y

0

)

v

1

+

f

y

′

(

x

0

,

y

0

)

v

2

=

{

f

x

′

(

x

0

,

y

0

)

,

f

y

′

(

x

0

,

y

0

)

}

∙

{

v

1

,

v

2

}

=

∇

f

∣

P

0

∙

v

=

∣

∇

f

∣

P

0

∣

⋅

∣

v

∣

cos

⁡

θ

\begin{aligned} \left.\frac{\partial f}{\partial v}\right|_{P_{0}} &=f_{x}^{\prime}\left(x_{0}, y_{0}\right) v_{1}+f_{y}^{\prime}\left(x_{0}, y_{0}\right) v_{2} \\ &=\left\{f_{x}^{\prime}\left(x_{0}, y_{0}\right), f_{y}^{\prime}\left(x_{0}, y_{0}\right)\right\} \bullet\left\{v_{1}, v_{2}\right\} \\ &=\left.\nabla f\right|_{P_{0}} \bullet v=|\nabla f|_{P_{0}}|\cdot| v \mid \cos \theta \end{aligned}

∂v∂f​

​P0​​​=fx′​(x0​,y0​)v1​+fy′​(x0​,y0​)v2​={fx′​(x0​,y0​),fy′​(x0​,y0​)}∙{v1​,v2​}=∇f∣P0​​∙v=∣∇f∣P0​​∣⋅∣v∣cosθ​

梯度下降法：

α

(

k

)

=

argmin

⁡

f

(

x

k

−

α

⋅

∇

f

(

x

(

k

)

)

)

\alpha_{(k)}=\operatorname{argmin} f\left(x^{k}-\alpha \cdot \nabla f\left(x^{(k)}\right)\right)

α(k)​=argminf(xk−α⋅∇f(x(k)))

梯度下降法的优缺点分析

优点：

（1）程序简单，计算量小；
（2）对初始点没有特别的要求；
（3）最速下降法是整体收敛的，且为线性收敛

缺点：

（1）它只在局部范围内具有“最速”属性， 对整体求解过程，它的下降速度是缓慢的；
（2）靠近极小值时速度减慢；
（3）可能会’之字型’地下降

核心代码和结果

代码的迭代结果：

迭代过程：

极小值-迭代次数趋势图像：

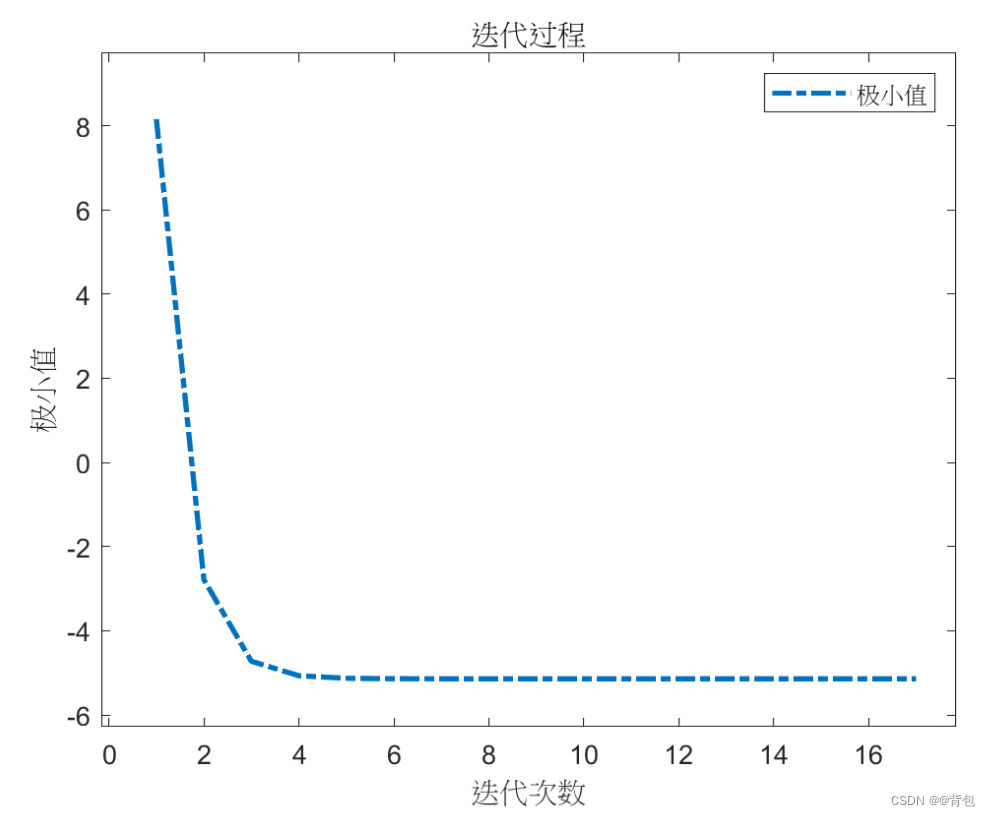
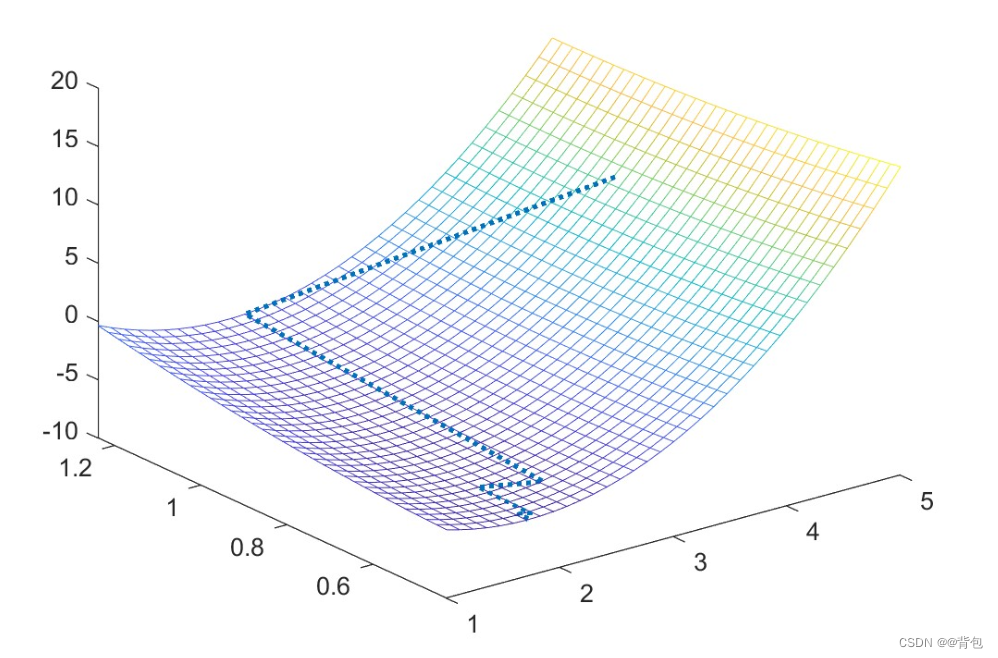
迭代结果在圆锥曲面上的可视化：

所求函数：

min

⁡

f

(

x

)

=

2

x

1

2

+

4

x

2

2

−

6

x

1

−

2

x

1

x

2

\min f(x)=2 x_{1}^{2}+4 x_{2}^{2}-6 x_{1}-2 x_{1} x_{2}

minf(x)=2x12​+4x22​−6x1​−2x1​x2​
主函数：

clc,clear;
syms x1 x2 s; %声明符号变量
f1 =2*x1^2+4*x2^2-6*x1-2*x1*x2;%设定目标函数
[k,f1,f2,f3]=grad(f1,x1,x2,s,[0,1],10^(-5));  %设定起始点[x1 x2]=[-2.5,4.25]和精度10^(-2)
[result]=sprintf('在 %d 次迭代后求出极小值\n',k);%在迭代多少次之后求出极小值
disp(result);
figure(1);
plot(1:k,f3); % 作出函数图像
title('迭代过程');%输出结果
xlabel('迭代次数');
ylabel('极小值');
figure(2);
plot3(f1,f2,f3); % 画出方程图像
hold on;
syms x1 x2; % 声明符号变量
f=2*x1^2+4*x2^2-6*x1-2*x1*x2;
fmesh(f);

梯度下降核心函数实现：

function  [iterator,f1,f2,f3] = grad(f,x1,x2,s,start_point,thereshold)
    iterator = 0;%迭代次数赋值初始化
    grad_f = [diff(f,x1) diff(f,x2)]; %计算f的梯度
    delta = subs(grad_f,[x1,x2],[start_point(1),start_point(2)]);
    %计算起点的梯度
    step=1; %设置初始步长为1
    current_point = start_point;%起点值赋给当前点
    %最速下降法的主循环，判断条件为：梯度的模与所给精度值进行比较
    while norm(delta) > thereshold
        iterator = iterator + 1;%迭代次数+1
        %一维探索 求最优步长（此时方向已知，步长s为变量）
        x_next = [current_point(1),current_point(2)] - s* delta/norm(delta);% 计算x（k+1）点，其中步长s为变量
        f_val = subs(f,[x1,x2],[x_next(1),x_next(2)]);% 将x值带入目标函数中
        step = abs(double(solve(diff(f_val,s)))); % 对s求一阶导，并加绝对值符号，得到最优步长的绝对值
        step = step(1);%更新步长
        %计算x（k+1）点
        current_point = double([current_point(1),current_point(2)] - step * delta/norm(delta));
        %计算x（k+1）点的梯度值
        delta = subs(grad_f,[x1,x2],[current_point(1),current_point(2)]);
        %计算函数值
        f_value = double(subs(f,[x1,x2],[current_point(1),current_point(2)]));
        %输出迭代计算过程
        result_string=sprintf('k=%d, x1=%.6f, x2=%.6f, step=%.6f f(x1,x2)=%.6f',iterator,current_point(1),current_point(2),step,f_value);
        f1(iterator)=current_point(1);
        f2(iterator)=current_point(2);
        f3(iterator)=f_value;
        disp(result_string);
    end
end

梯度算法的局限性及其优化

神经网络中，梯度的搜索是使用最为广泛的参数寻优方法，在此类方法美些视策解出发,代寻找最优参数值、每次送代中，我们先计算设置函数当前点的梯度，并根据梯度确定搜索方向。

在搜索过程中，我们可能会遇到陷入局部最小的问题，如果误差函数具有多个局部极小,则不能保证找到的解是全局最小，对后一种情形,我们称参数寻优陷入了局部极小,这显然不是我们所希望的。

在现实任务中,人们常采用以下策略来试图“跳出”局部极小 从而进-步接近全局最小:

• 以多组不同参数值初始化多个神经网络,按标准方法训练后,取其中误差最小的解作为最终参数.这相当于从多个不同的初始点开始搜索,这样就可能陷入不同的局部极小，从中进行选择有可能获得更接近全局最小的结果.
  但是也会造成“跳出”全局最小
• 使用“模拟退火”技术，模拟退火在每一步都以一定的概率接受比当前解更差的结果,从而有助于“跳出”局部极小.在每步迭代过程中、接受“你优解》的概率要随着时间的摊移而逐渐降低。从而保证算法稳定
• 使用随机梯度下降.与标准梯度下降法精确计算梯度不同,随机梯度下降法在计算梯度时加入了随机因素。于是，即便陷入局部极小点,它计算出的梯度仍可能不为零,这样就有机会跳出局部极小继续搜索。