【LeetCode贪心#06】加油站(股票买卖变种)

加油站

力扣题目链接(opens new window)

在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。

说明:

• 如果题目有解，该答案即为唯一答案。
• 输入数组均为非空数组，且长度相同。
• 输入数组中的元素均为非负数。

示例 1: 输入:

• gas = [1,2,3,4,5]
• cost = [3,4,5,1,2]

输出: 3 解释:

• 从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
• 开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
• 开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
• 开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
• 开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
• 开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
• 因此，3 可为起始索引。

示例 2: 输入:

• gas = [2,3,4]
• cost = [3,4,3]
• 输出: -1
• 解释: 你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油。开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油。开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油。你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。因此，无论怎样，你都不可能绕环路行驶一周。

思路

以

• gas = [2,5,2,3,5]
• cost = [1,2,8,2,4] 为例

如图所示，我们可以先将到达每个下标时的剩余油量计算出来

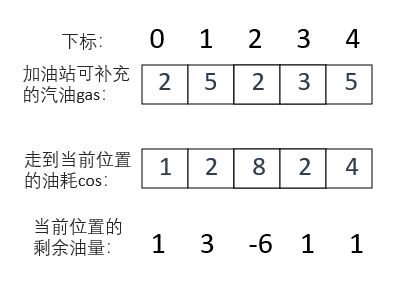
开始时，我们在下标0处的加油站补充2的汽油，走到该位置需要消耗1的汽油，因此此时剩余油量为1

接下来，走到下标1处的加油站补充5的汽油，走到该位置需要消耗2的汽油，因此此时剩余油量为1 + 5 - 2 = 4

同理计算出行驶到的每个位置的剩余油量

此时不难发现，如果从下标0出发的话，到下标2时剩余油量已经不够了

所以不能从下标0出发

而从下标3出发似乎可以恰好走完一圈，在下标2处没油然后停止

这里的规律就是：计算出所有位置的油耗，然后我们从油量变为负数的位置之后的一个位置出发，就可以走完一圈

用贪心的方式描述就是：

局部最优：使用一个变量curGasSum累加行驶到当前位置的油量剩余，一旦该变量小于0，假设当前位置为i，那么下一次的起始位置至少要是i+1，因为从i之前开始一定不行。

全局最优：找到一定可以跑完一圈的起始位置

代码

步骤如下：

1、定义变量

• 统计行驶到当前位置的油量剩余
• 统计遍历过程中的所有油量（可能为负值）
• 记录开始行驶的位置

2、遍历下标位置（相当于遍历加油站,只是下标和gas一样）

3、分别计算当前剩余油量和总油量

4、判断当前油量是否为负（遇到负数油量，说明该位置之前的位置都不可能支撑走完一圈，要从该位置之后开始走）

• 更新出发位置到负值的后一位
• 重置当前油量curGasSum

5、判断totalGas是否为负（如果遍历完所有可能出发的下标后，油耗为负数，则说明从哪走都不行，直接返回-1）

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        //定义一些变量
        int curGasSum = 0;//统计行驶到当前位置的油量剩余
        int totalGas = 0;//统计遍历过程中的所有油量（可能为负值）
        int beginIndex = 0;//开始行驶的位置，即出发位置
        for(int i = 0; i < gas.size(); ++i){//遍历gas（相当于遍历加油站,只是下标和gas一样）
            curGasSum += gas[i] - cost[i];//当前剩余油量
            totalGas += gas[i] - cost[i];//需要分开计算
            if(curGasSum < 0){//遇到负数油量，说明该位置之前的位置都不可能支撑走完一圈，要从该位置之后开始走
                beginIndex = i + 1;//更新出发位置
                curGasSum = 0;//重置当前油量
            }
        }
        if(totalGas < 0) return -1;//如果遍历完所有可能出发的下标后，油耗为负数，则说明从哪走都不行
        return beginIndex;
    }
};