神经网络优化篇：详解为超参数选择合适的范围（Using an appropriate scale to pick hyperparameters）

为超参数选择合适的范围

假设要选取隐藏单元的数量\(n^{[l]}\)，假设，选取的取值范围是从50到100中某点，这种情况下，看到这条从50-100的数轴，可以随机在其取点，这是一个搜索特定超参数的很直观的方式。或者，如果要选取神经网络的层数，称之为字母\(L\)，也许会选择层数为2到4中的某个值，接着顺着2，3，4随机均匀取样才比较合理，还可以应用网格搜索，会觉得2，3，4，这三个数值是合理的，这是在几个在考虑范围内随机均匀取值的例子，这些取值还蛮合理的，但对某些超参数而言不适用。

看看这个例子，假设在搜索超参数\(a\)（学习速率），假设怀疑其值最小是0.0001或最大是1。如果画一条从0.0001到1的数轴，沿其随机均匀取值，那90%的数值将会落在0.1到1之间，结果就是，在0.1到1之间，应用了90%的资源，而在0.0001到0.1之间，只有10%的搜索资源，这看上去不太对。

反而，用对数标尺搜索超参数的方式会更合理，因此这里不使用线性轴，分别依次取0.0001，0.001，0.01，0.1，1，在对数轴上均匀随机取点，这样，在0.0001到0.001之间，就会有更多的搜索资源可用，还有在0.001到0.01之间等等。

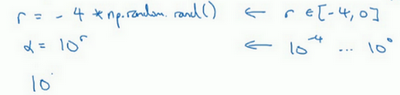
所以在Python中，可以这样做，使r=-4*np.random.rand()，然后\(a\)随机取值，$ a =10^{r}\(，所以，第一行可以得出\)r \in [ 4,0]\(，那么\)a \in[10^{-4},10]$，所以最左边的数字是\(10^{-4}\)，最右边是\(10^{0}\)。

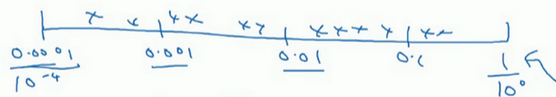
更常见的情况是，如果在\(10^{a}\)和\(10^{b}\)之间取值，在此例中，这是\(10^{a}\)（0.0001），可以通过\(\operatorname{}{0.0001}\)算出\(a\)的值，即-4，在右边的值是\(10^{b}\)，可以算出\(b\)的值\(\operatorname{}1\)，即0。要做的就是在\([a,b]\)区间随机均匀地给\(r\)取值，这个例子中\(r \in \lbrack - 4,0\rbrack\)，然后可以设置\(a\)的值，基于随机取样的超参数\(a =10^{r}\)。

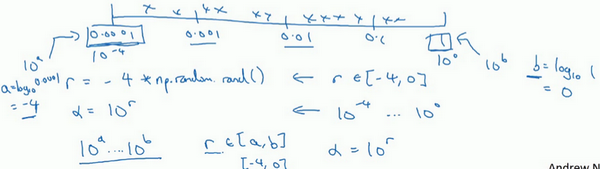
所以总结一下，在对数坐标下取值，取最小值的对数就得到\(a\)的值，取最大值的对数就得到\(b\)值，所以现在在对数轴上的\(10^{a}\)到\(10^{b}\)区间取值，在\(a\)，\(b\)间随意均匀的选取\(r\)值，将超参数设置为\(10^{r}\)，这就是在对数轴上取值的过程。

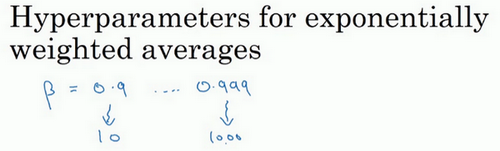
最后，另一个棘手的例子是给\(\beta\) 取值，用于计算指数的加权平均值。假设认为\(\beta\)是0.9到0.999之间的某个值，也许这就是想搜索的范围。记住这一点，当计算指数的加权平均值时，取0.9就像在10个值中计算平均值，有点类似于计算10天的温度平均值，而取0.999就是在1000个值中取平均。

所以和上面的内容类似，如果想在0.9到0.999区间搜索，那就不能用线性轴取值，对吧？不要随机均匀在此区间取值，所以考虑这个问题最好的方法就是，要探究的是\(1-\beta\)，此值在0.1到0.001区间内，所以会给\(1-\beta\)取值，大概是从0.1到0.001，应用之前介绍的方法，这是\(10^{-1}\)，这是\(10^{-3}\)，值得注意的是，在之前的内容里，把最小值写在左边，最大值写在右边，但在这里，颠倒了大小。这里，左边的是最大值，右边的是最小值。所以要做的就是在\([-3,-1]\)里随机均匀的给r取值。设定了\(1- \beta = 10^{r}\)，所以\(\beta = 1-10^{r}\)，然后这就变成了在特定的选择范围内超参数随机取值。希望用这种方式得到想要的结果，在0.9到0.99区间探究的资源，和在0.99到0.999区间探究的一样多。

所以，如果想研究更多正式的数学证明，关于为什么要这样做，为什么用线性轴取值不是个好办法，这是因为当\(\beta\) 接近1时，所得结果的灵敏度会变化，即使\(\beta\)有微小的变化。所以\(\beta\) 在0.9到0.9005之间取值，无关紧要，的结果几乎不会变化。

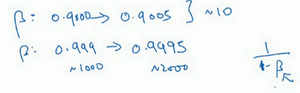
但\(\beta\)值如果在0.999到0.9995之间，这会对的算法产生巨大影响，对吧？在这两种情况下，是根据大概10个值取平均。但这里，它是指数的加权平均值，基于1000个值，现在是2000个值，因为这个公式\(\frac{1}{1- \beta}\)，当\(\beta\)接近1时，\(\beta\)就会对细微的变化变得很敏感。所以整个取值过程中，需要更加密集地取值，在\(\beta\) 接近1的区间内，或者说，当\(1-\beta\) 接近于0时，这样，就可以更加有效的分布取样点，更有效率的探究可能的结果。

希望能帮助选择合适的标尺，来给超参数取值。如果没有在超参数选择中作出正确的标尺决定，别担心，即使在均匀的标尺上取值，如果数值总量较多的话，也会得到还不错的结果，尤其是应用从粗到细的搜索方法，在之后的迭代中，还是会聚焦到有用的超参数取值范围上。