最大堆（MaxHeap）

性质

• 二叉堆是一颗完全二叉树，而完全二叉树是把元素排列成树的形状。
• 堆中某个节点的值总不大于其父节点的值最大堆（相应的可以定于最小堆）

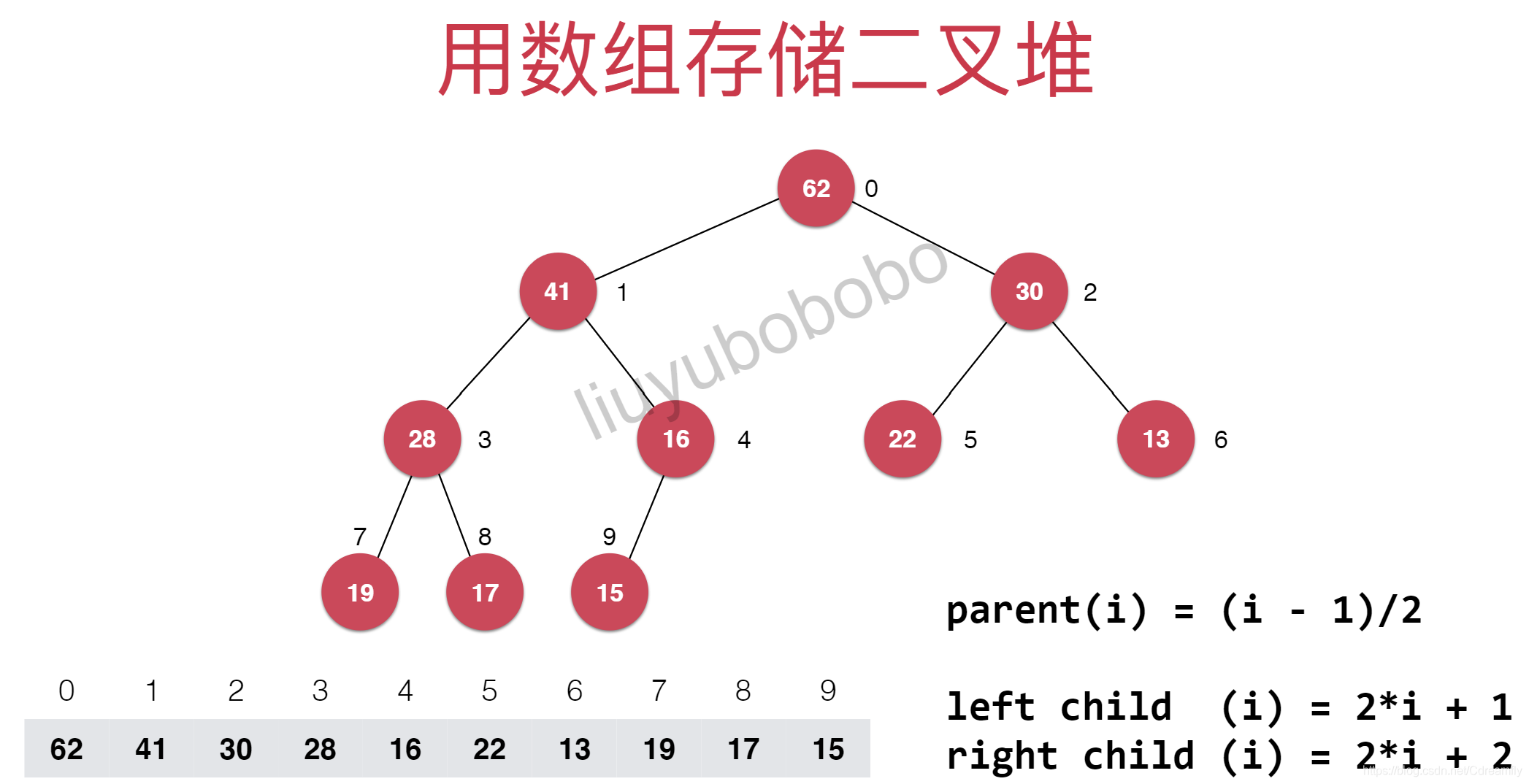
// 返回完全二叉树的数组表示中，一个索引所表示的元素的父亲节点的索引
constexpr int parent(const int index) const {
    if (index == 0) {
        throw new NoParent();
    }
    return (index - 1) / 2;
}

// 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
constexpr int leftChild(const int index) const {
    return (index * 2) + 1;
}

// 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
constexpr int rightChild(const int index) const {
    return (index * 2) + 2;
}

可以先阅读底层动态数组Array

添加

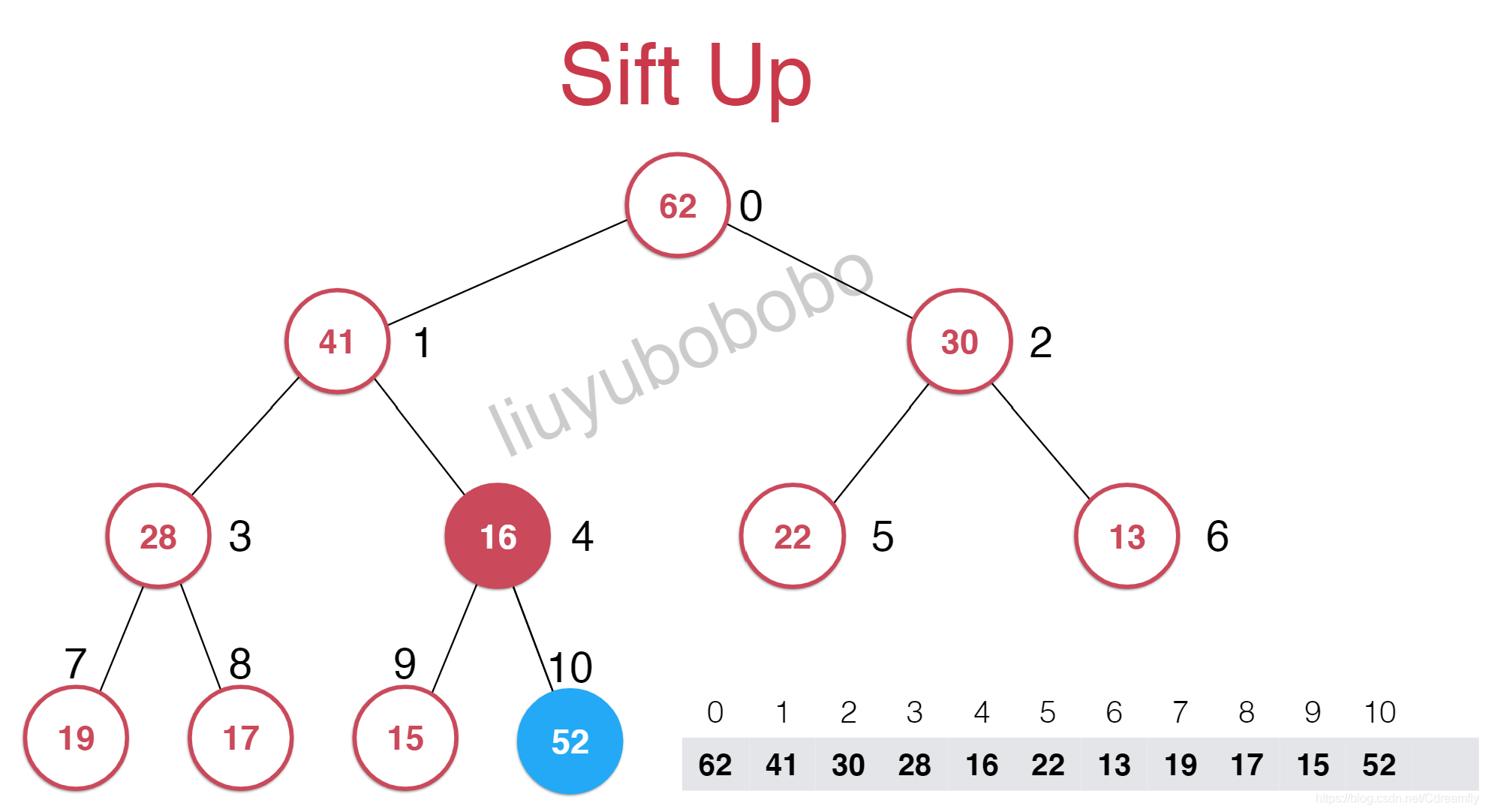
首先我们堆中的数据使用数组排列的，所以添加一个元素就是在层序遍历的最右端，也就是最下面一层的最后添加一个元素。但是以数组来看就是在索引为10的地方添加一个元素。

void add(const T &e) {
	data->addLast(e);	//在数组的末尾添加元素
	shiftUp(data->getSize() - 1);	//上浮添加元素的索引
}

• 时间复杂度O(logn)

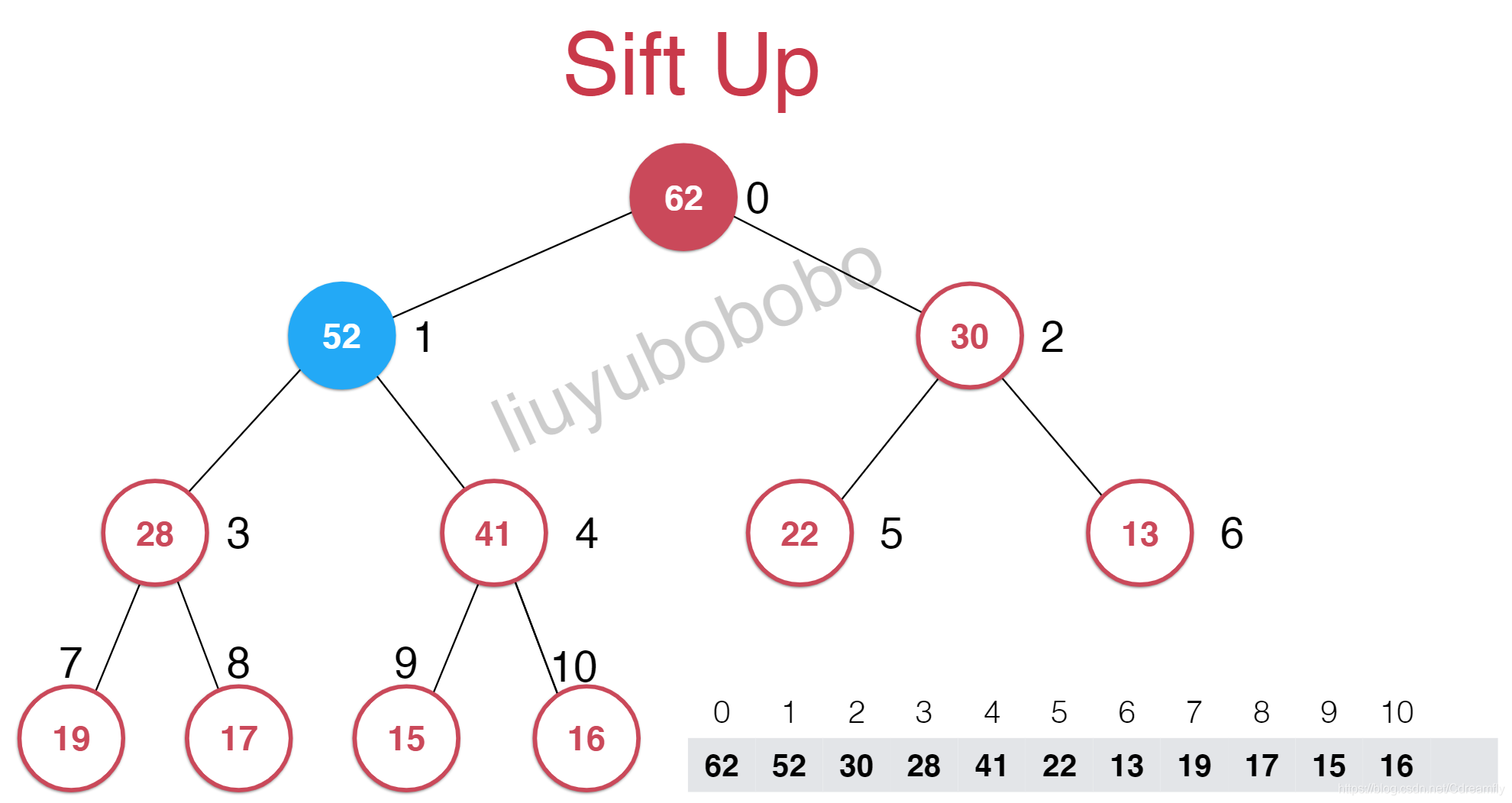
但是添加的元素不符最大堆的性质，索引我需要一些调整，而这个调整就是一个上浮的过程。

void shiftUp(int index) {
	//如果传入索引小于等于0并且父元素大于等于子元素则停止循环
   while (index > 0 && data->get(index) > data->get(parent(index))) {
        data->swap(index, parent(index));	//位置交换
        index = parent(index);	//把父节点的索引给子节的
    }
}

取出最大元素

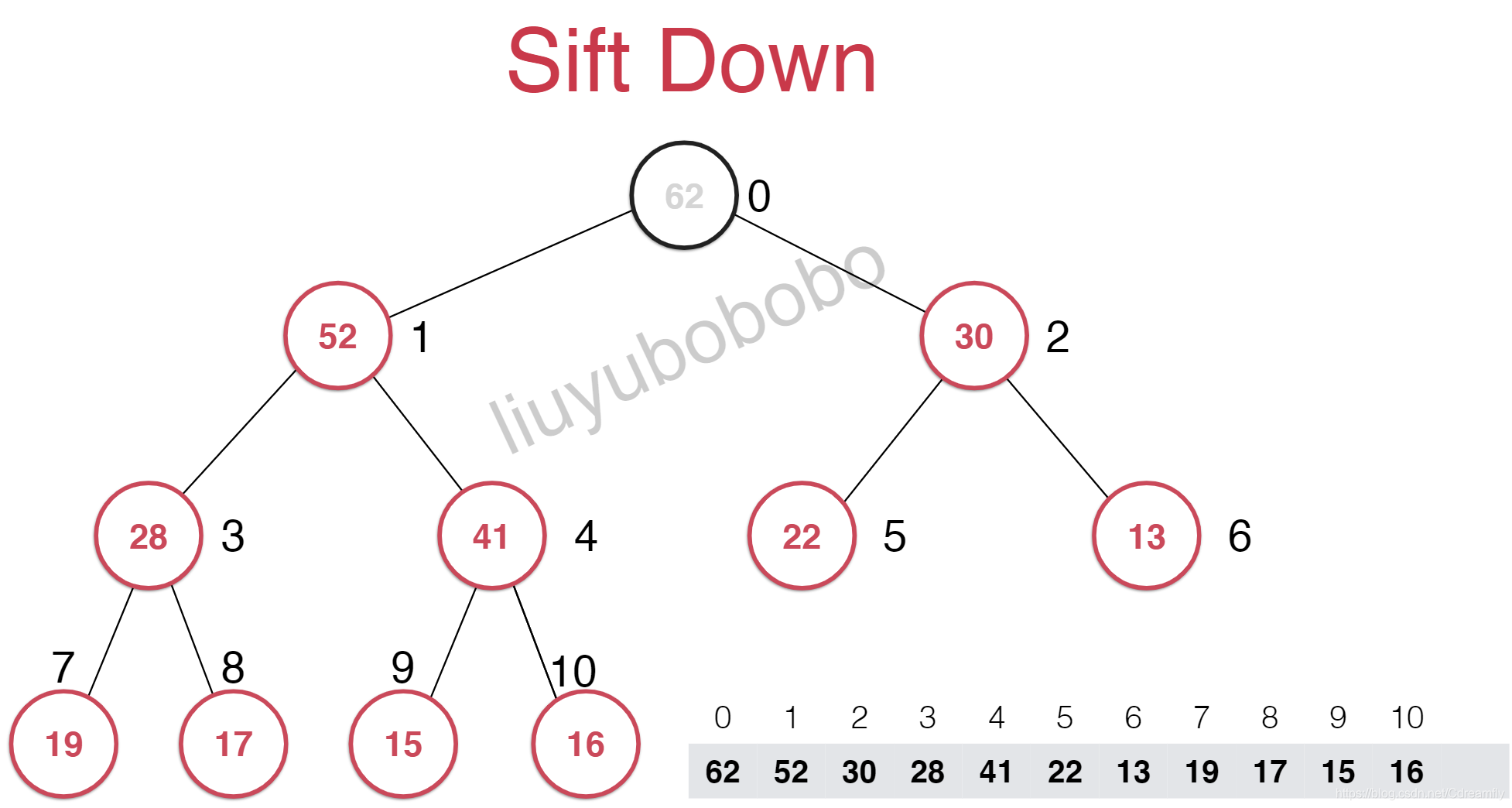
最大堆的最大元素就是其根节点元素，取出的操作只能取出这个元素，对于数组来说，根结点就是索引为0的元素。



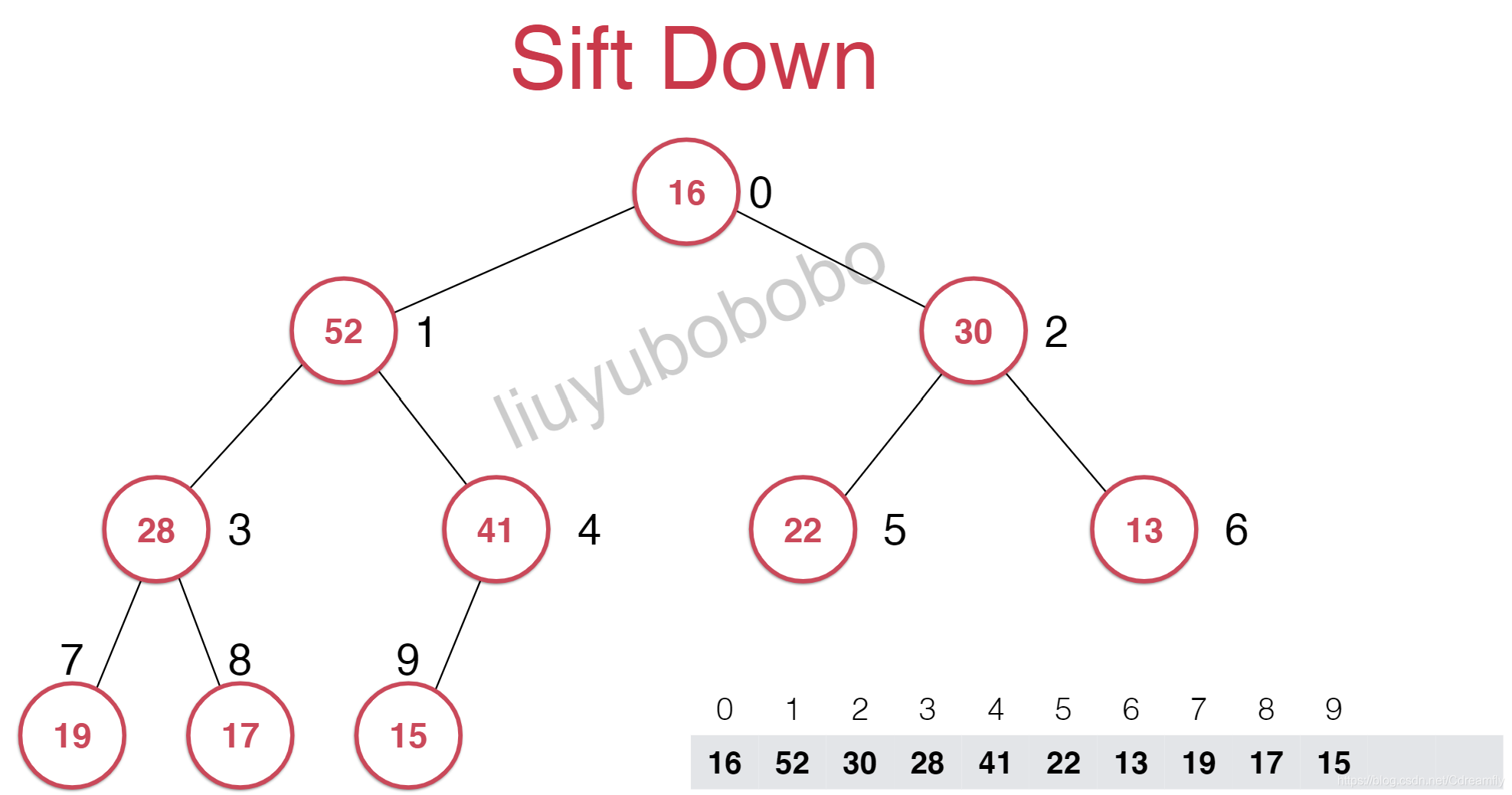
我们把堆中最后一个元素顶到堆顶去，然后再把最后一个元素删除。然而这样就又不符合最大堆的性质。

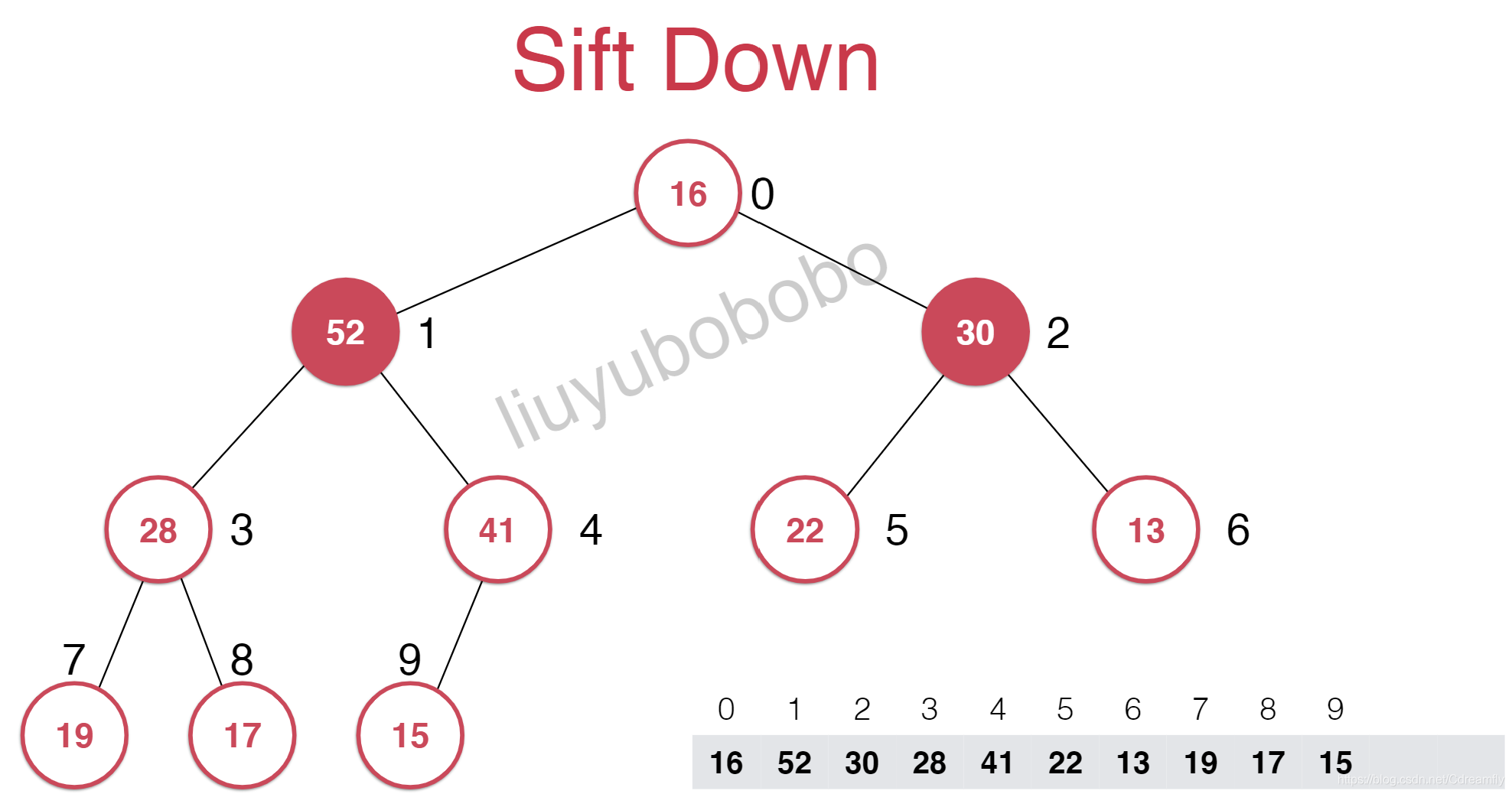
这样的话，其不大于它的子节点，此时又要进行调整，这个调整的过程叫做下沉。在这个过程中每次需要下沉的时候都要和它的两个孩子进行比较，选择其中较大的进行交换位置。

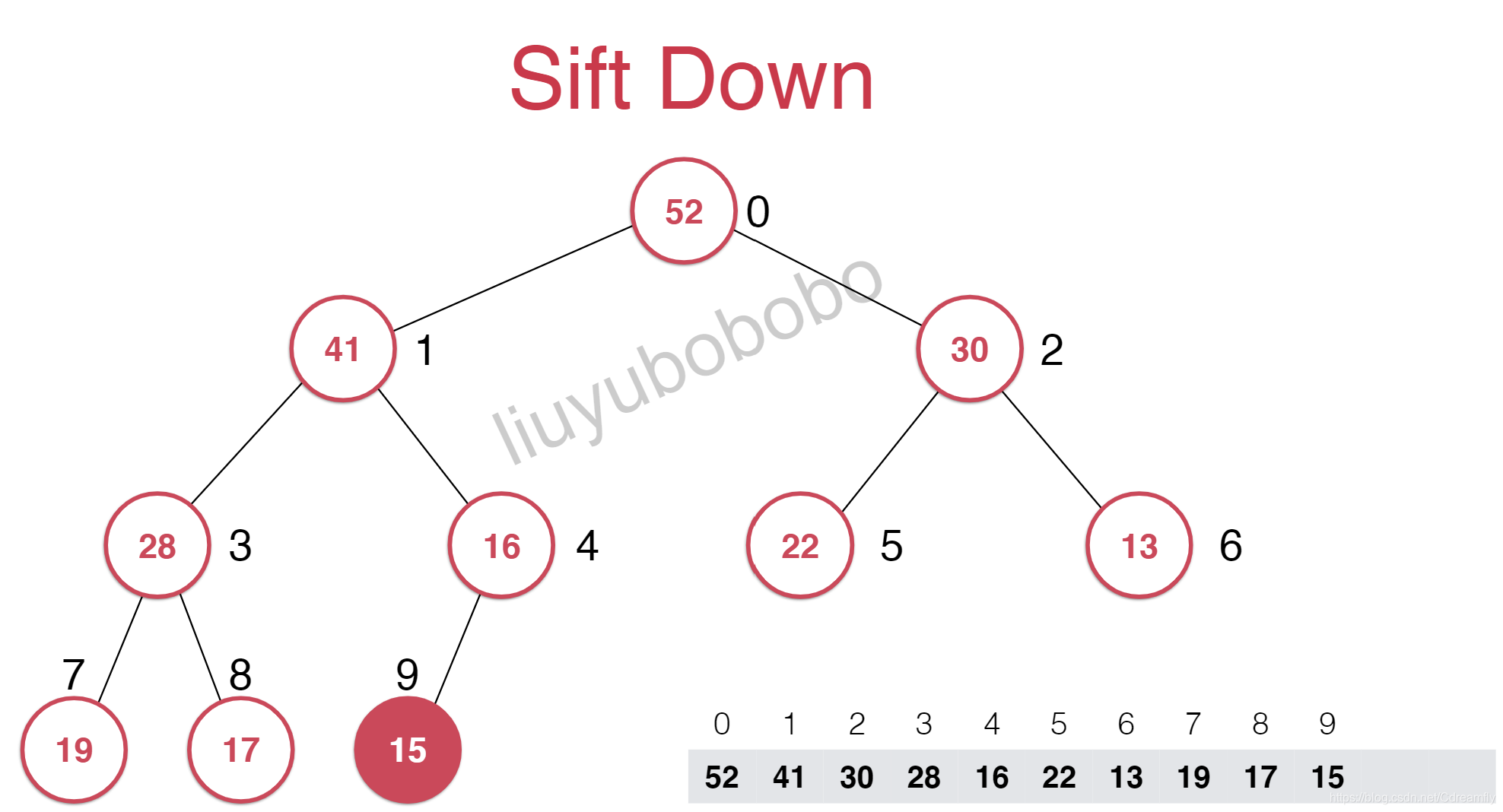
• 时间复杂度O(logn)

//返回最大的元素
 T findMax() const {
    if (data->isEmpty()) {
        throw Empty();
    }
    return data->get(0);
}
//取出最大的元素
T extractMax() {
    T ret = findMax();
    data->swap(0, data->getSize() - 1);
    data->removeLast();
    shiftDown(0);
    return ret;
}

//下沉
void shiftDown(int k) {
    while (leftChild(k) < data->getSize()) {
        int j = leftChild(k);
        //j保存的是左右孩子中较大的元素索引
        if (j + 1 < data->getSize() && data->get(j + 1) > data->get(j)) {
            j = rightChild(k);
        }
        //如果子节点小于等于父节点了，就结束
        if (data->get(k) > data->get(j)) {
            break;
        }
        data->swap(k, j);
        k = j;
    }
}

取出堆中最大的元素，并替换成元素e

• 时间复杂度O(logn)

T replace(T e) {
    T ret = findMax();
    data->set(0, e);
    shiftDown(0);
    return ret;
}

Heapify

将n个元素逐个插入到一个空堆中，算法复杂度是O(nlogn)，Heapify的过程，算法复杂度是O(n)。

MaxHeap(T arr[], const int n) {
    data = new Array<T>(arr, n);
    for (int i = parent(n - 1); i >= 0; --i) {
        shiftDown(i);
    }
}

对比使用与不适用Heapify代码

#include <iostream>
#include "MaxHeap.h"
#include <cassert>

template<typename T>
double testHeap(T testData[], int n, bool isHeapify) {
    clock_t startTime = clock();
    MaxHeap<T> *maxHeap;
    if (isHeapify) {
        maxHeap = new MaxHeap<T>(testData, n);
    } else {
        maxHeap = new MaxHeap<T>();
        for (int i = 0; i < n; ++i) {
            maxHeap->add(testData[i]);
        }
    }

    T *arr = new T[n];
    for (int j = 0; j < n; ++j) {
        arr[j] = maxHeap->extractMax();
    }

    for (int k = 1; k < n; ++k) {
        assert(arr[k - 1] >= arr[k]);
    }
    std::cout << "Test MaxHeap completed." << std::endl;
    clock_t endTime = clock();
    return double(endTime - startTime) / CLOCKS_PER_SEC;
}

int main() {
    int n = 5000000;
    int *testData = new int[n];
    for (int i = 0; i < n; ++i) {
        testData[i] = rand() % INT32_MAX;
    }
    double time1 = testHeap(testData, n, false);
    std::cout << "Without heapify :" << time1 << " s " << std::endl;
    double time2 = testHeap(testData, n, true);
    std::cout << "With heapify :" << time2 << " s " << std::endl;
    return 0;
}

代码清单

//
// Created by cheng on 2021/7/10.
//

#ifndef MAXHEAP_MAXHEAP_H
#define MAXHEAP_MAXHEAP_H

#include "Array.h"

template<typename T>
class MaxHeap {
public:

    class NoParent {
    };

    class Empty {
    };

    MaxHeap() {
        data = new Array<T>();
    }

    ~MaxHeap() {
        delete data;
        data = nullptr;
    }

    MaxHeap(const int capacity) {
        data = new Array<T>(capacity);
    }

    MaxHeap(T arr[], const int n) {
        data = new Array<T>(arr, n);
        for (int i = parent(n - 1); i >= 0; --i) {
            shiftDown(i);
        }
    }

    constexpr int getSize() const {
        return data->getSize();
    }

    constexpr bool isEmpty() const {
        return data->isEmpty();
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的父亲节点的索引
    constexpr int parent(const int index) const {
        if (index == 0) {
            throw new NoParent();
        }
        return (index - 1) / 2;
    }

    void add(const T &e) {
        data->addLast(e);
        shiftUp(data->getSize() - 1);
    }
	//返回最大元素
    T findMax() const {
        if (data->isEmpty()) {
            throw Empty();
        }
        return data->get(0);
    }
	//取出最大的元素
    T extractMax() {
        T ret = findMax();
        data->swap(0, data->getSize() - 1);
        data->removeLast();
        shiftDown(0);
        return ret;
    }
    //取出堆中最大的元素，并替换成元素e
	T replace(T e) {
        T ret = findMax();
        data->set(0, e);
        shiftDown(0);
        return ret;
	}

    void print() {
        data->print();
    }

private:

    void shiftDown(int k) {
        while (leftChild(k) < data->getSize()) {
            int j = leftChild(k);
            if (j + 1 < data->getSize() && data->get(j + 1) > data->get(j)) {
                j = rightChild(k);
            }
            if (data->get(k) > data->get(j)) {
                break;
            }
            data->swap(k, j);
            k = j;
        }
    }

    void shiftUp(int index) {
        while (index > 0 && data->get(index) > data->get(parent(index))) {
            data->swap(index, parent(index));
            index = parent(index);
        }
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
    constexpr int leftChild(const int index) const {
        return (index * 2) + 1;
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
    constexpr int rightChild(const int index) const {
        return (index * 2) + 2;
    }

private:
    Array<T> *data;
};

#endif //MAXHEAP_MAXHEAP_H