1. Vectors and Linear Combinations

1.1 Vectors

We have n separate numbers $v_1、v_2、v_3,...,v_n$，that produces a n-dimensional vector $v$，and $v$ is represented by an arrow.

\[v=\left[
\begin{matrix}
v_1 \\
v_2 \\
.\\
.\\
.\\
v_n
\end{matrix}
\right] = (v_1,v_2,...,v_n)
\]

Two-dimensional vector ：$v = \left[\begin{matrix} v_1 \\ v_2 \end{matrix}\right]$ and $w = \left[\begin{matrix} w_1 \\ w_2 \end{matrix}\right]$

Vector Addition : $v + w = \left[\begin{matrix} v_1 + w_1 \\ v_2 + w_2\end{matrix}\right]$
Scalar Multiplication : $cv = \left[\begin{matrix} cv_1 \\ cv_2 \end{matrix}\right]$，c is scalar.

1.2 Linear Combinations

Multiply $v$ by $c$ and multiply $w$ by $d$，the sum of $cv$ and $dw$ is a linear combination : $cv + dw$.

We can visualize $v + w$ using arrows，for example：

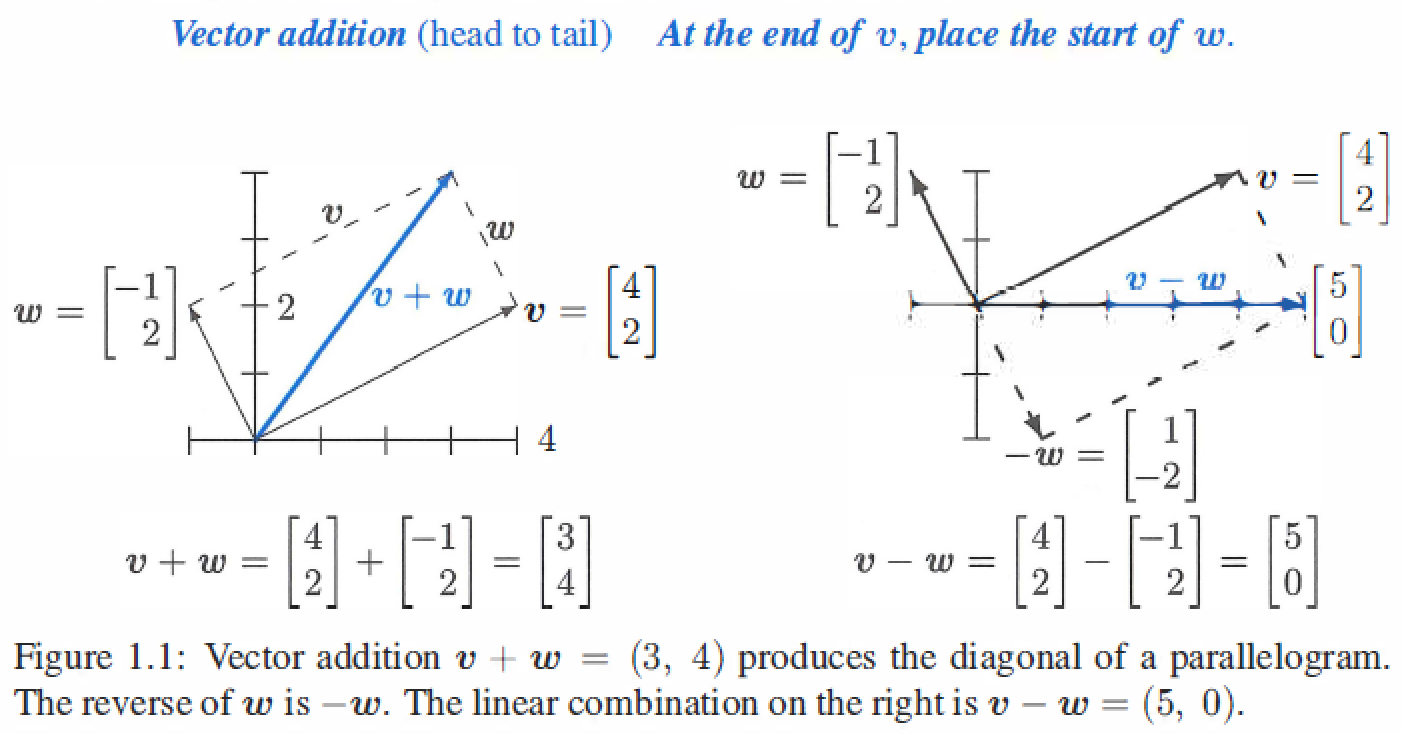
The combinations can fill Line、Plane 、or 3-dimensional space:

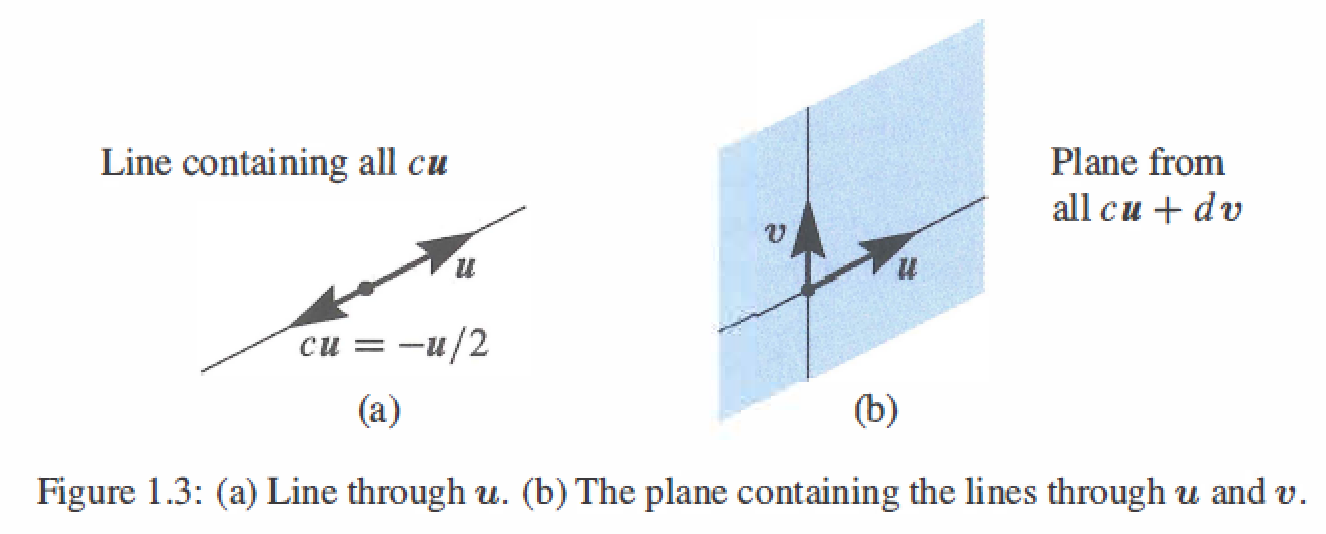
The combinations $cu$ fill a line through origin.
The combinations $cu + dv$ fill a plane throught origin
The combinations $cu + dv +ew$ fill three-dimensional space throught origin.

1.3 Lengths and Dot Products

Dot Product/ Inner Product: $v \cdot w = v_1w_1 + v_2w_2$，where $v = (v_1, v_2) $ and $w=(w_1, w_2)$ ，the dot product $w \cdot v$ equals $v \cdot w$

Length : $||v|| = \sqrt{v \cdot v} = (v_1^2 + v_2^2 + v_3^2 +...+ v_n^2)^{1/2}$

Unit vector : $u = v /||v||$ is a unit vector in the same direction as $v$，length =1

Perpendicular vector : $v \cdot w = 0$

Cosine Formula : if $v$ and $w$ are nonzero vectors then $\frac{v \cdot w}{||v|| \ ||w||} = cos \theta$ , $\theta$ is the angle between $v$ and $w$

Schwarz Inequality : $|v \cdot w| \leq ||v|| \ ||w||$

Triangel Inequality : $||v + w|| \leq ||v|| + ||w||$

1.4 Matrices

1、$A = \left[ \begin{matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{matrix}\right]$ is a 3 by 2 matrix : m=2 rows and n=2 columns

2、$Ax = b $ is a linear combination of the columns A

3、 Combination of the vectors : $Ax = x_1\left[ \begin{matrix} 1 \\ -1 \\ 0 \end{matrix} \right] + x_2\left[ \begin{matrix} 0 \\ 1 \\ -1 \end{matrix} \right] + x_3\left[ \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \right] = \left[ \begin{matrix} x_1 \\ x_2-x_1 \\ x_3-x_2 \end{matrix} \right]$

4、Matrix times Vector : $Ax = \left[ \begin{matrix} 1&0&0\ -1&1&0 \ 0&-1&1 \end{matrix} \right] \left[ \begin{matrix} x_1\ x_2 \ x_3 \end{matrix} \right]= \left[ \begin{matrix} x_1 \ x_2-x_1 \ x_3-x_2 \end{matrix} \right] $

5、Linear Equation : Ax = b --> $\begin{matrix} x_1 = b_1 \\ -x_1 + x_2 = b_2 \\ -x_2 + x_3 = b_3 \end{matrix}$

6、Inverse Solution : $x = A^{-1}b$ -- > $\begin{matrix} x_1 = b_1 \\ x_2 = b_1 + b_2 \\ x_3 =b_1 + b_2 + b_3 \end{matrix}$, when A is an invertible matrix

7、Independent columns : Ax = 0 has one solution, A is an invertible matrix, the column vectors of A are independent. (example: $u,v,w$ are independent，No combination except $0u + 0v + 0w = 0$ gives $b=0$)

8、Dependent columns : Cx = 0 has many solutions, C is a singular matrix, the column vectors of C are dependent. (example: $u,v,w^*$ are dependent，other combinations like $au + cv + dw^*$ gives $b=0$)